
Question and Answers Forum
Question Number 127501 by slahadjb last updated on 30/Dec/20
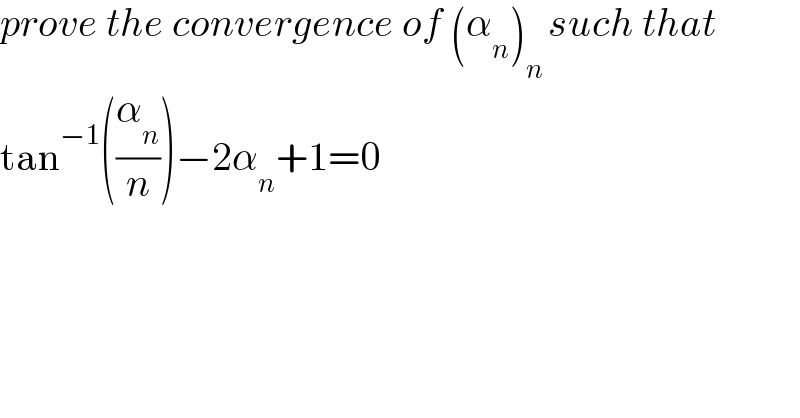
Answered by mindispower last updated on 31/Dec/20
![⇒2a_n =1+tan^− ((a_n /n))⇒a_n ∈[−(π/4)+(1/2),(π/4)+(1/2)] bounded⇒lim_(n→∞) (a_n /n)→0 ⇒tan^− ((α_n /n))+1⇒1sinceg: x→tan^(−1) (x)+1 is continus 2a_n =g((a_n /n)),2a_n →g(0)=1 a_n →(1/2)](Q127599.png)
Commented by slahadjb last updated on 31/Dec/20
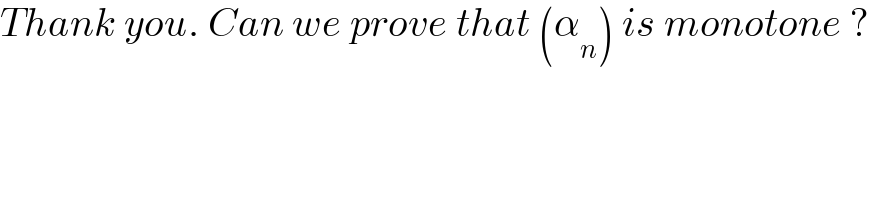
Commented by mindispower last updated on 31/Dec/20
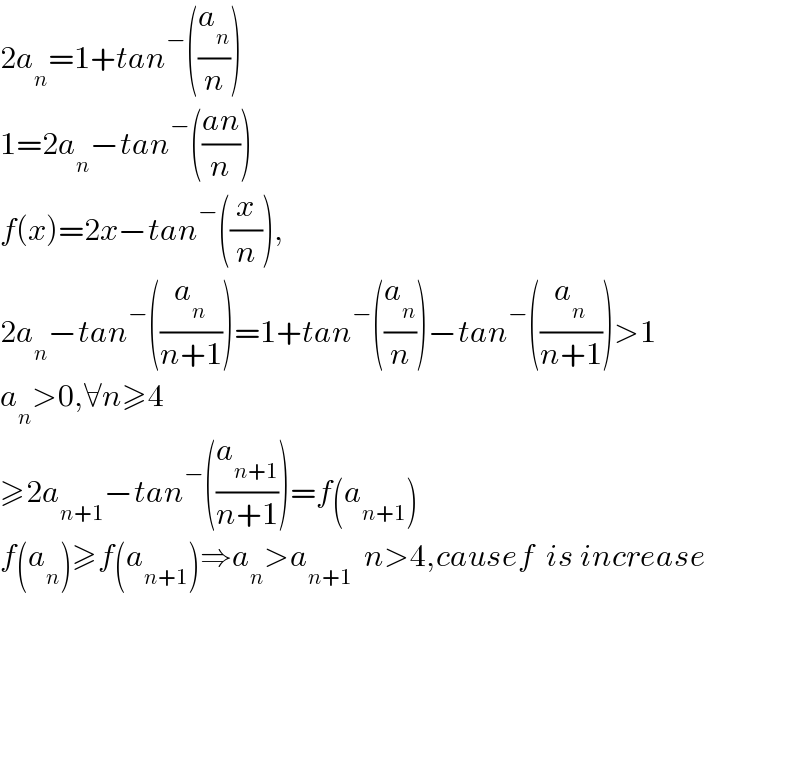
Commented by slahadjb last updated on 31/Dec/20
Commented by mindispower last updated on 31/Dec/20

