
Question and Answers Forum
Question Number 127567 by mathocean1 last updated on 30/Dec/20

Commented by malwan last updated on 01/Jan/21
![a=(√3)(((√3)/2) + (i/2)) = [(√3) , (π/6)] a^n = [((√3))^n , ((nπ)/6)]∈R ⇒((nπ)/6) = mπ ; m∈N ⇒n = 6m ; m∈N b = 1+i = [(√2) , (π/4)] ⇒b^n = [((√2))^n , ((nπ)/4)]∈iR ⇒((nπ)/4) = (2m +1)(π/2) ⇒n= 4m + 2 ; m∈N](Q127694.png)
Answered by Ar Brandon last updated on 30/Dec/20
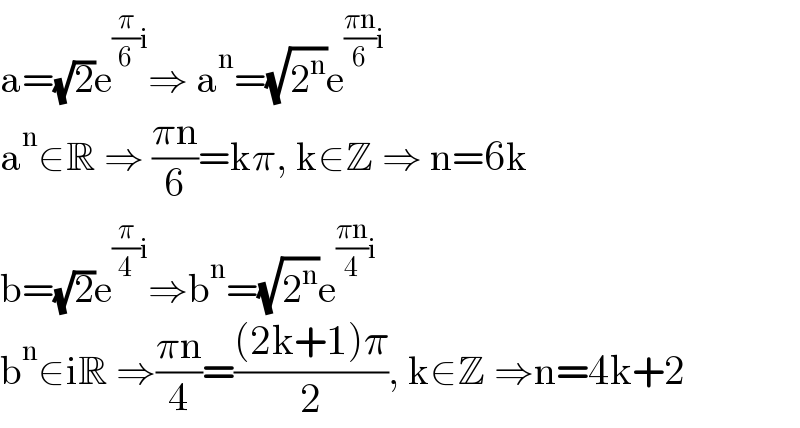
Answered by mr W last updated on 31/Dec/20
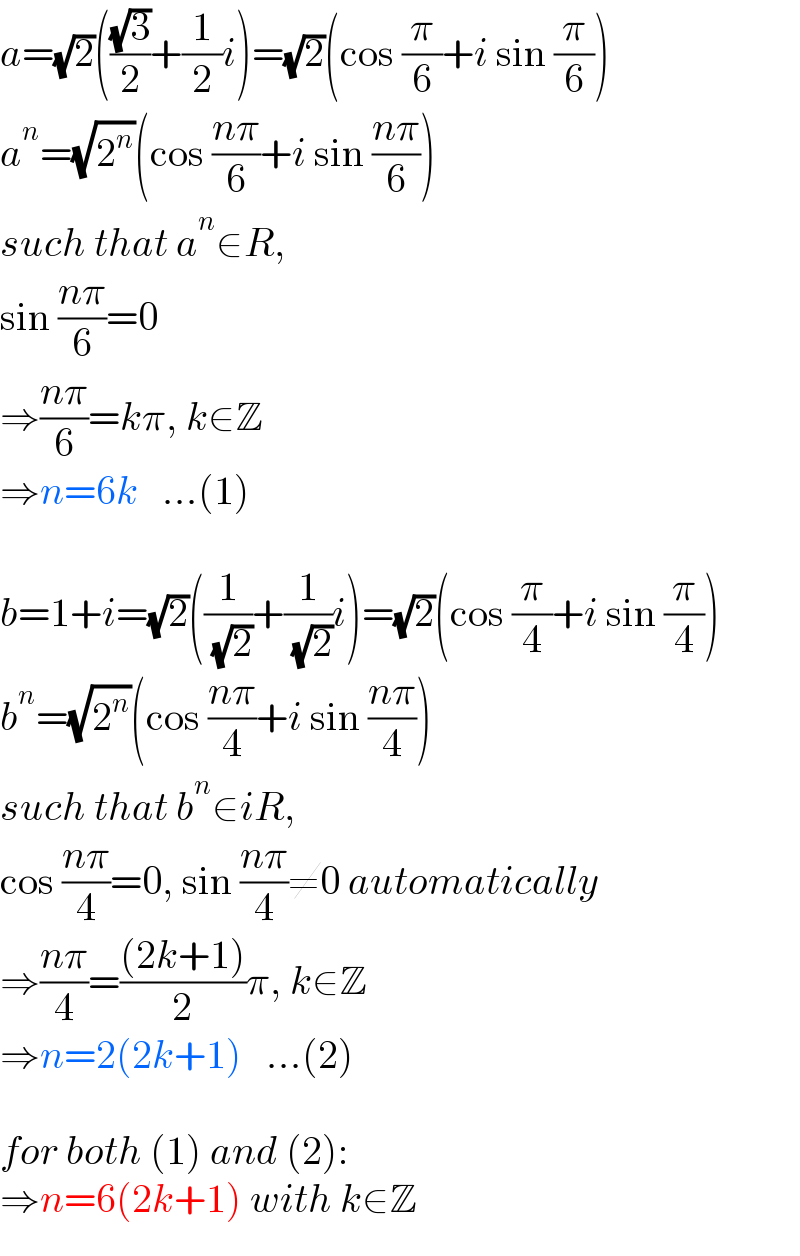
| ||
Question and Answers Forum | ||
Question Number 127567 by mathocean1 last updated on 30/Dec/20 | ||
 | ||
Commented by malwan last updated on 01/Jan/21 | ||
![a=(√3)(((√3)/2) + (i/2)) = [(√3) , (π/6)] a^n = [((√3))^n , ((nπ)/6)]∈R ⇒((nπ)/6) = mπ ; m∈N ⇒n = 6m ; m∈N b = 1+i = [(√2) , (π/4)] ⇒b^n = [((√2))^n , ((nπ)/4)]∈iR ⇒((nπ)/4) = (2m +1)(π/2) ⇒n= 4m + 2 ; m∈N](Q127694.png) | ||
Answered by Ar Brandon last updated on 30/Dec/20 | ||
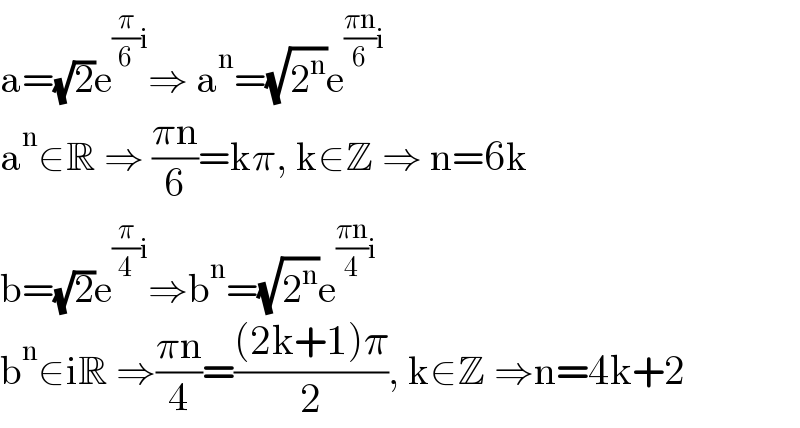 | ||
| ||
Answered by mr W last updated on 31/Dec/20 | ||
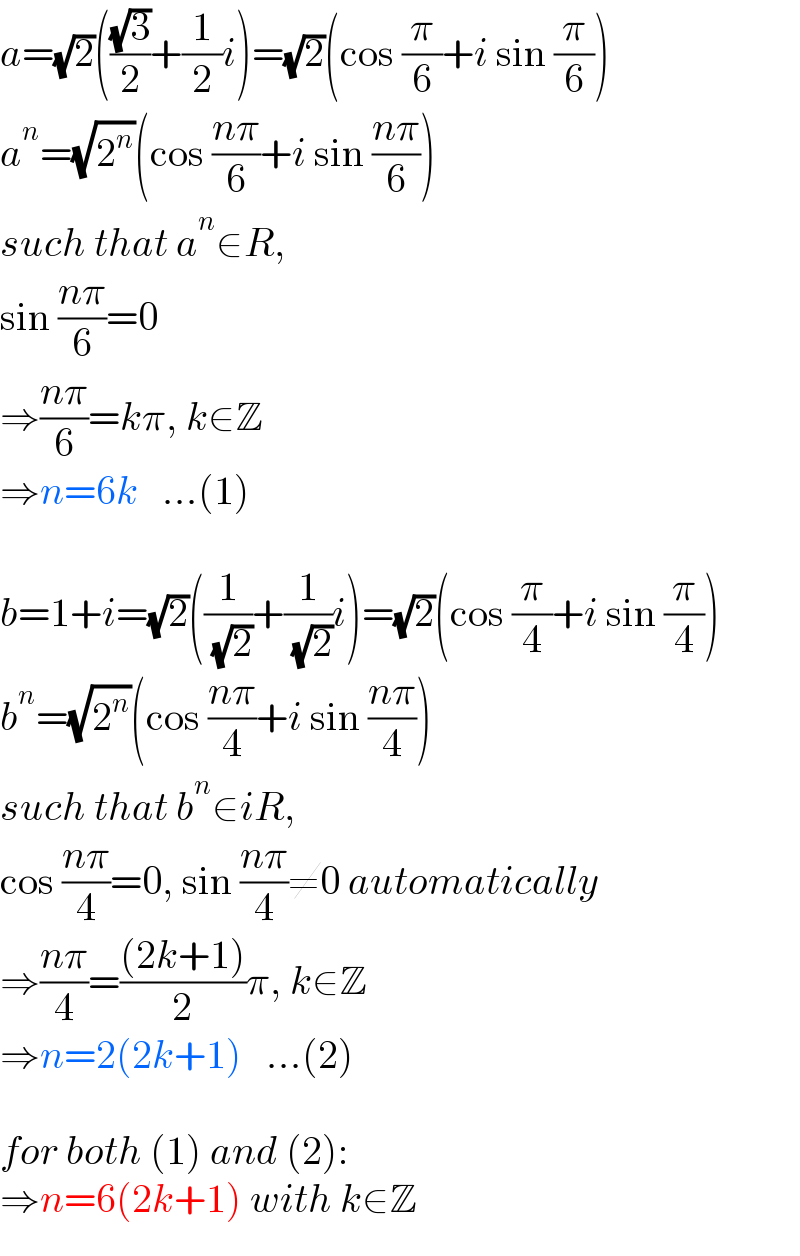 | ||
| ||