
Question and Answers Forum
Question Number 128007 by ajfour last updated on 03/Jan/21
![Can anyone find any error in my attempt to improve upon the Cardano′s cubic formula.. or as an alternate to the trigonometric solution... here it goes: X^3 −pX−q=0 let (X/( (√p))) = x ; and with (q/(p(√p))) = c , x^3 −x−c=0 let x=(k+1)(p+q) =(p+kq) + (kp+q) p^3 +k^3 q^3 +3kpq(p+kq)+ k^3 p^3 +q^3 +3kpq(kp+q) −(p+kq)−(kp+q)=c ⇒ (1+k^3 )(p^3 +q^3 )+ (p+kq)(3kpq−1)+ (kp+q)(3kpq−1)= c let 3kpq=1 ⇒ p^3 +q^3 =(c/(1+k^3 )) & p^3 q^3 =(1/(27k^3 )) ; hence p^3 , q^3 = (c/(2(1+k^3 )))±(√((c^2 /(4(1+k^3 )^2 ))−(1/(27k^3 )))) lets choose upon a value of k such that D=0 ⇒ 4(1+k^3 )^2 =27c^2 k^3 .....(I) (just a quadratic..) first for c^2 >(8/(27)) we always can get two real k values, and even p=q then. x=(k+1)(p+q) = 2(k+1)p x=2(k+1)[(c/(2(1+k^3 )))]^(1/3) but simply pq=(1/(3k)) hence x=2(k+1)p = ((2(k+1))/( (√(3k)))) . ________________________ even for c=1 i dint get a correct answer, please help error-freeing it. (Thanks!)](Q128007.png)
Commented by MJS_new last updated on 04/Jan/21
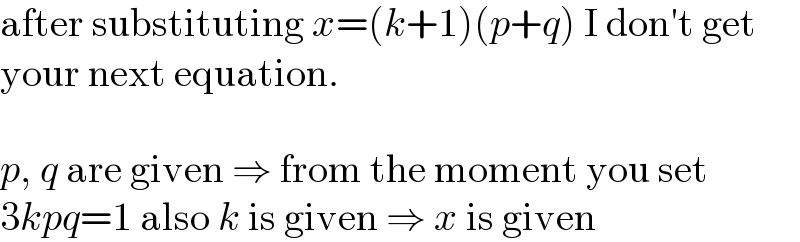
Commented by ajfour last updated on 04/Jan/21
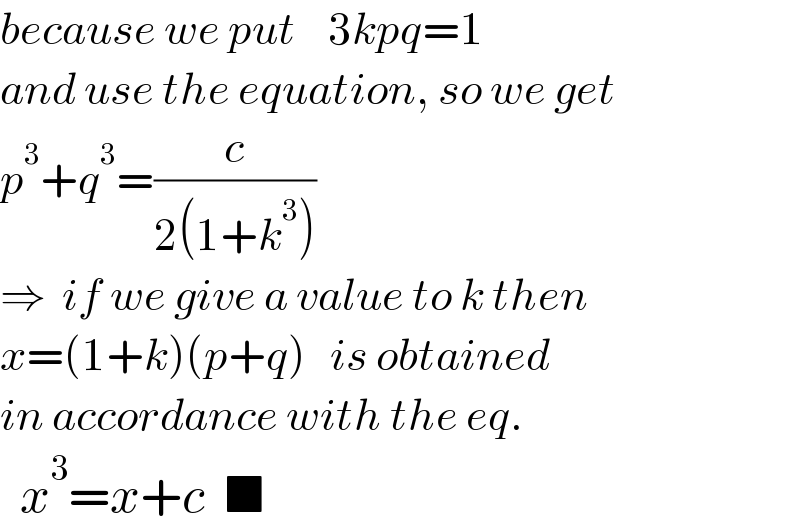
| ||
Question and Answers Forum | ||
Question Number 128007 by ajfour last updated on 03/Jan/21 | ||
![Can anyone find any error in my attempt to improve upon the Cardano′s cubic formula.. or as an alternate to the trigonometric solution... here it goes: X^3 −pX−q=0 let (X/( (√p))) = x ; and with (q/(p(√p))) = c , x^3 −x−c=0 let x=(k+1)(p+q) =(p+kq) + (kp+q) p^3 +k^3 q^3 +3kpq(p+kq)+ k^3 p^3 +q^3 +3kpq(kp+q) −(p+kq)−(kp+q)=c ⇒ (1+k^3 )(p^3 +q^3 )+ (p+kq)(3kpq−1)+ (kp+q)(3kpq−1)= c let 3kpq=1 ⇒ p^3 +q^3 =(c/(1+k^3 )) & p^3 q^3 =(1/(27k^3 )) ; hence p^3 , q^3 = (c/(2(1+k^3 )))±(√((c^2 /(4(1+k^3 )^2 ))−(1/(27k^3 )))) lets choose upon a value of k such that D=0 ⇒ 4(1+k^3 )^2 =27c^2 k^3 .....(I) (just a quadratic..) first for c^2 >(8/(27)) we always can get two real k values, and even p=q then. x=(k+1)(p+q) = 2(k+1)p x=2(k+1)[(c/(2(1+k^3 )))]^(1/3) but simply pq=(1/(3k)) hence x=2(k+1)p = ((2(k+1))/( (√(3k)))) . ________________________ even for c=1 i dint get a correct answer, please help error-freeing it. (Thanks!)](Q128007.png) | ||
Commented by MJS_new last updated on 04/Jan/21 | ||
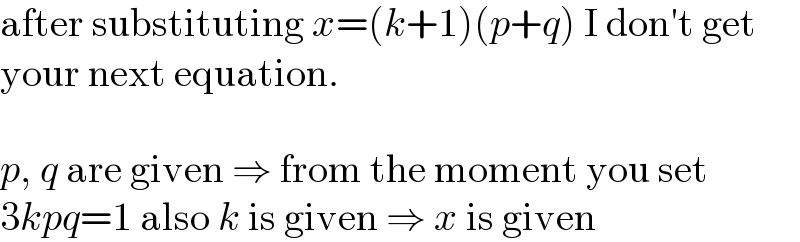 | ||
Commented by ajfour last updated on 04/Jan/21 | ||
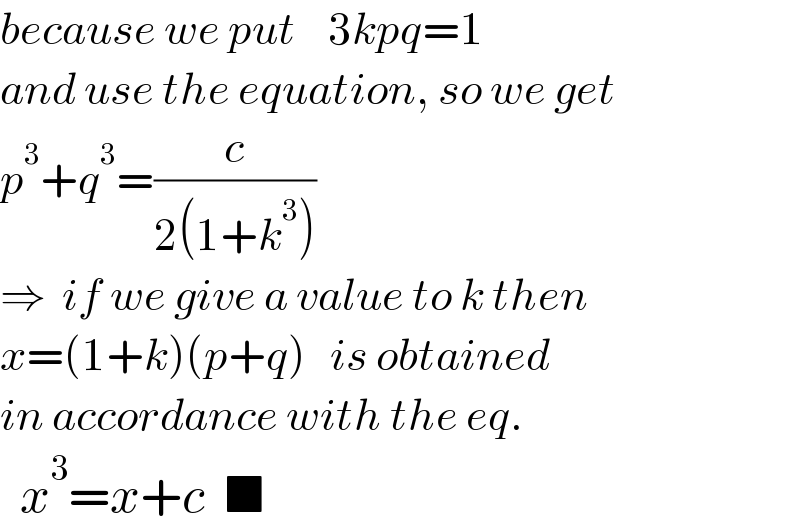 | ||