Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 128048 by bramlexs22 last updated on 04/Jan/21

$$\underset{\mathrm{n}=0}{\sum ^{\mathrm{\infty }}}\frac{{(-1)}^{\mathrm{n}}}{8\mathrm{n}+3}=?$$

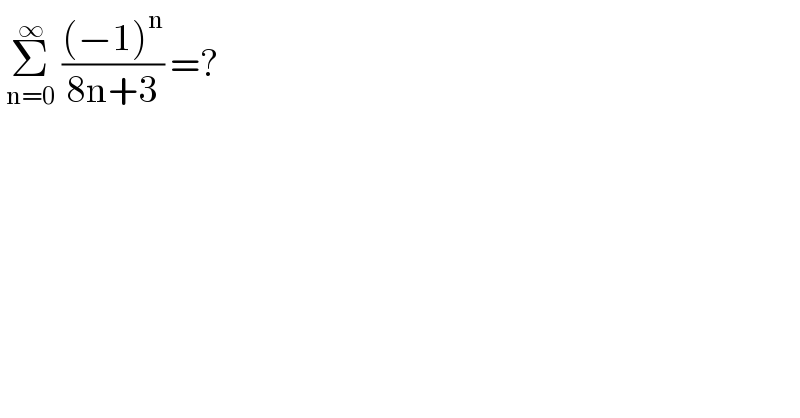
Answered by Olaf last updated on 04/Jan/21

$$\mathrm{L}(\lambda ,\alpha ,s)=\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{e^{2i\pi \lambda n}}{{(n+\alpha )}^s}\mathrm{or}\mathrm{Lerch}(\lambda ,\alpha ,s)$$$$\left(\mathrm{zeta}\mathrm{Lerch}\mathrm{function}\right)$$$$\mathrm{Let}\mathrm{S}=\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{{(-1)}^n}{8n+3}$$$$\mathrm{S}=\frac{1}{8}\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{e^{i\pi n}}{{(n+\frac{3}{8})}^1}=\frac{1}{8}\mathrm{L}(\frac{1}{2},\frac{3}{8},1)$$$$\mathrm{We}\mathrm{have}\mathrm{too}:$$$$\mathrm{\Phi }(z,s,\alpha )=\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{z^n}{{(n+\alpha )}^s}\mathrm{or}\mathrm{LerchPhi}(z,s,\alpha )$$$$\left(\mathrm{transcendent}\mathrm{Lerch}\mathrm{function}\right)$$$$\mathrm{S}=\frac{1}{8}\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{{(-1)}^n}{{(n+\frac{3}{8})}^1}=\frac{1}{8}\mathrm{\Phi }(-1,1,\frac{3}{8})$$$$\mathrm{S}\approx 0,2738982192$$

Commented by bramlexs22 last updated on 04/Jan/21

I just found out about the lerch zeta function

Commented by bramlexs22 last updated on 04/Jan/21

$$\mathrm{how}\mathrm{about}\underset{\mathrm{n}=0}{\sum ^{\mathrm{\infty }}}\frac{{(-1)}^{\mathrm{n}}}{8\mathrm{n}+5}\mathrm{sir}?$$

Commented by Olaf last updated on 04/Jan/21

$$\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{{(-1)}^n}{8n+5}=\frac{1}{8}\mathrm{LerchPhi}(-1,1,\frac{5}{8})$$$$\approx 0,1511562039$$

Commented by bramlexs22 last updated on 04/Jan/21

$$\mathrm{sir}\mathrm{how}\mathrm{you}\mathrm{get}\approx 0.1511562039?$$$$\mathrm{by}\mathrm{software}\mathrm{sir}\mathrm{or}\mathrm{calculator}?$$

Answered by mindispower last updated on 04/Jan/21

$$=\mathrm{\Sigma }\frac{1}{16(n+\frac{3}{16})}-\frac{1}{16(n+\frac{11}{16})}$$$$=\mathrm{\Sigma }\frac{2}{256(n+\frac{3}{16})(n+\frac{11}{16})}$$$$=\frac{1}{16}(\mathrm{\Psi }\left(\frac{3}{16}\right)-\mathrm{\Psi }\left(\frac{11}{16}\right))$$$$4lose$$$$2ndway{\int }_0^1{x}^2{(-x^8)}^{n}dx=\frac{{(-1)}^n}{8n+1}dx$$$$justusingbasicresults\mathrm{\Sigma }{(-z)}^n=\frac{1}{1+z}$$$$and{Z}^n+1=0\Rightarrow Z=e^{i\left(\frac{2k+1}{n}\right)\pi }$$$$\Rightarrow \sum _{n⩾0}{\int }_0^1{x}^2.{(-x^8)}^{n}dx=\sum _{n⩾0}\frac{{(-1)}^n}{8n+3}$$$$\iff {\int }_0^1\frac{x^2}{1+x^8}dx=\sum _{n⩾0}\frac{{(-1)}^n}{8n+3}$$$$x^8+1=\underset{k=0}{\prod ^7}(X-e^{i\left(\frac{(2k+1)\pi }{8}\right))})$$$$=\underset{k=0}{\prod ^3}(X^2-2cos\left(\frac{2k+1}{8}\pi \right)X+1)$$$$decompositionwegetelementry\int \frac{dx}{X^2+aX+1}$$$$findvalueofintegrals$$

Answered by Dwaipayan Shikari last updated on 04/Jan/21

$$\underset{n=0}{\sum ^{\mathrm{\infty }}}\frac{{(-1)}^n}{8n+3}={\int }_0^1\sum ^{\mathrm{\infty }}{(-1)}^n{x}^{8n+2}dx$$$$={\int }_0^1\frac{x^2}{1+x^8}dxwecansolvethisAfterdecomposing$$$$$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com