
Question and Answers Forum
Question Number 128052 by bramlexs22 last updated on 04/Jan/21
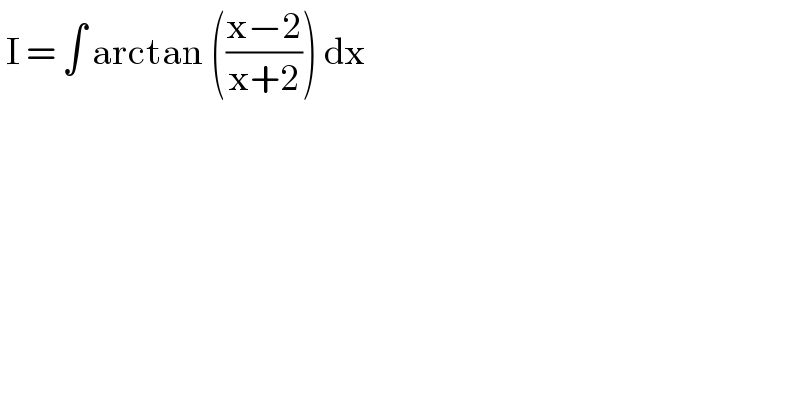
Answered by liberty last updated on 04/Jan/21
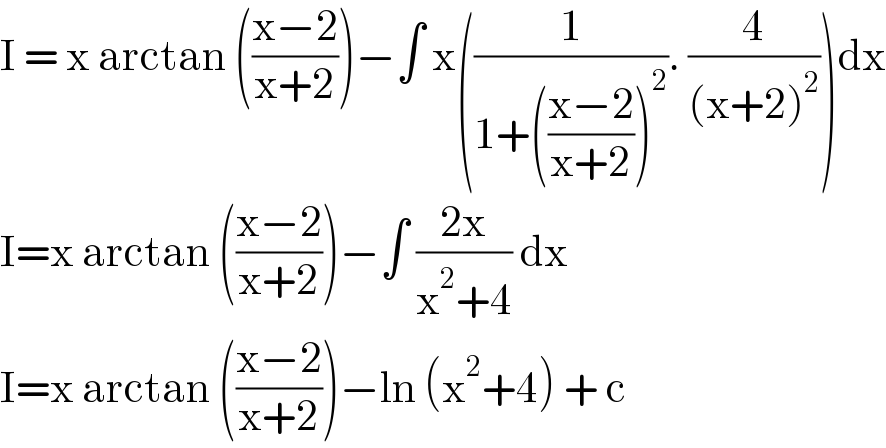
Answered by Olaf last updated on 04/Jan/21
![I = ∫arctan(((x−2)/(x+2)))dx I = −∫arctan(((1−(x/2))/(1+(x/2))))dx (1) I = −∫[arctan(1)−arctan((x/2))]dx (2) I = −(π/4)x+xarctan((x/2))−∫((2x)/(x^2 +4))dx I = −(π/4)x+xarctan((x/2))−ln(x^2 +4)+C (1) : artan(−u) = −arctanu (2) arctanu−arctanv = arctan(((u−v)/(1+uv)))](Q128054.png)
Answered by bramlexs22 last updated on 04/Jan/21

| ||
Question and Answers Forum | ||
Question Number 128052 by bramlexs22 last updated on 04/Jan/21 | ||
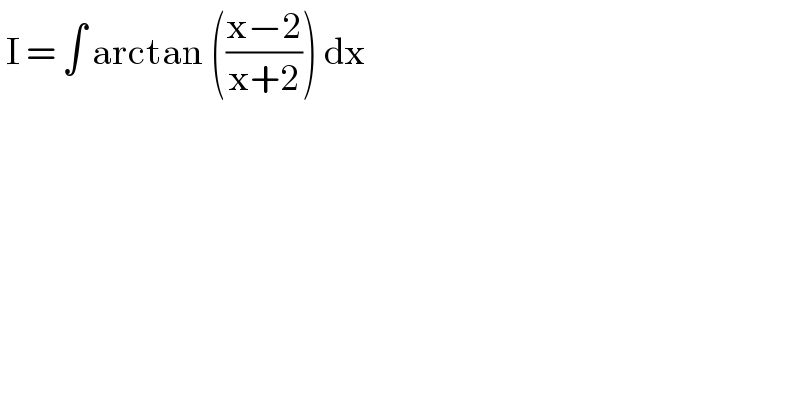 | ||
Answered by liberty last updated on 04/Jan/21 | ||
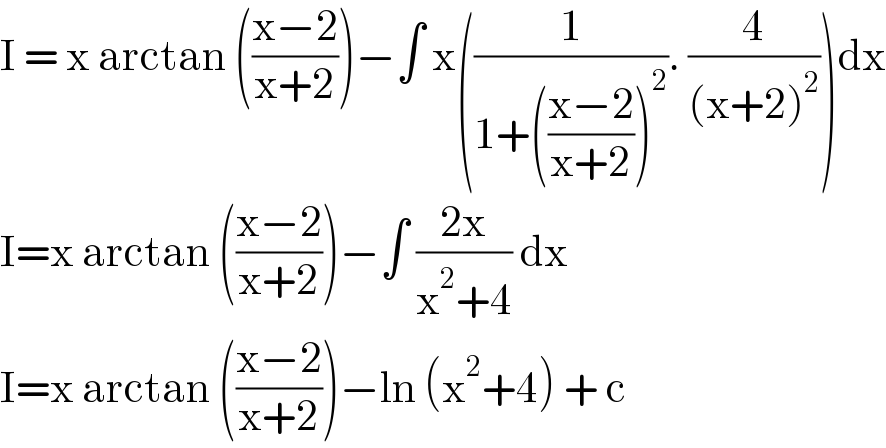 | ||
| ||
Answered by Olaf last updated on 04/Jan/21 | ||
![I = ∫arctan(((x−2)/(x+2)))dx I = −∫arctan(((1−(x/2))/(1+(x/2))))dx (1) I = −∫[arctan(1)−arctan((x/2))]dx (2) I = −(π/4)x+xarctan((x/2))−∫((2x)/(x^2 +4))dx I = −(π/4)x+xarctan((x/2))−ln(x^2 +4)+C (1) : artan(−u) = −arctanu (2) arctanu−arctanv = arctan(((u−v)/(1+uv)))](Q128054.png) | ||
| ||
Answered by bramlexs22 last updated on 04/Jan/21 | ||
 | ||