
Question and Answers Forum
Question Number 128068 by benjo_mathlover last updated on 04/Jan/21
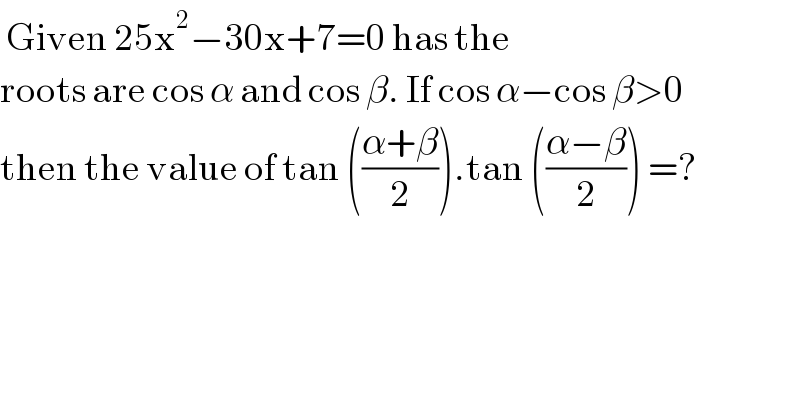
Answered by bemath last updated on 04/Jan/21

Answered by Dwaipayan Shikari last updated on 04/Jan/21

| ||
Question and Answers Forum | ||
Question Number 128068 by benjo_mathlover last updated on 04/Jan/21 | ||
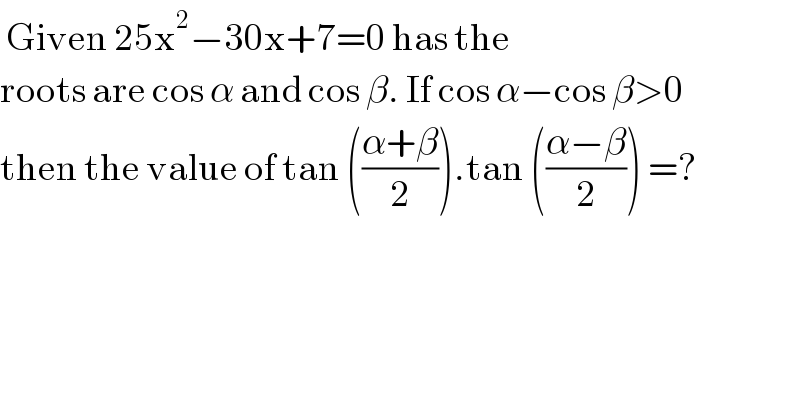 | ||
Answered by bemath last updated on 04/Jan/21 | ||
 | ||
| ||
Answered by Dwaipayan Shikari last updated on 04/Jan/21 | ||
 | ||
| ||