Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 128122 by Dwaipayan Shikari last updated on 04/Jan/21

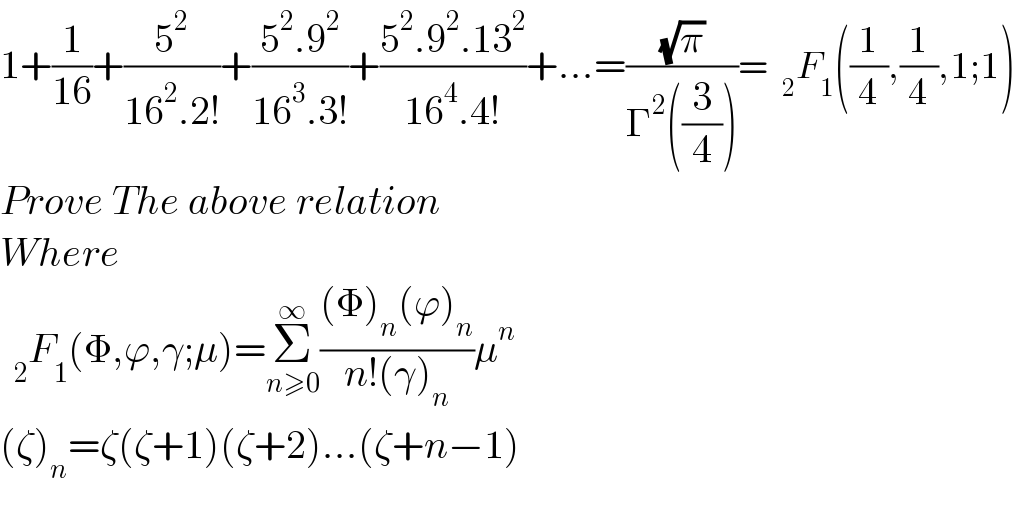
1+(1/(16))+(5^2 /(16^2 .2!))+((5^2 .9^2 )/(16^3 .3!))+((5^2 .9^2 .13^2 )/(16^4 .4!))+...=((√π)/(Γ^2 ((3/4))))=F_1 ((1/4),(1/4),1;1) Prove The above relation Where F_1 (Φ,ϕ,γ;μ)=Σ_(n≥0) ^∞ (((Φ)_n (ϕ)_n )/(n!(γ)_n ))μ^n (ζ)_n =ζ(ζ+1)(ζ+2)...(ζ+n−1)

$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{16}}+\frac{\mathrm{5}^{\mathrm{2}} }{\mathrm{16}^{\mathrm{2}} .\mathrm{2}!}+\frac{\mathrm{5}^{\mathrm{2}} .\mathrm{9}^{\mathrm{2}} }{\mathrm{16}^{\mathrm{3}} .\mathrm{3}!}+\frac{\mathrm{5}^{\mathrm{2}} .\mathrm{9}^{\mathrm{2}} .\mathrm{13}^{\mathrm{2}} }{\mathrm{16}^{\mathrm{4}} .\mathrm{4}!}+...=\frac{\sqrt{\pi}}{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)}={F}_{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{4}},\frac{\mathrm{1}}{\mathrm{4}},\mathrm{1};\mathrm{1}\right) \\ $$$${Prove}\:{The}\:{above}\:{relation} \\ $$$${Where} \\ $$$${F}_{\mathrm{1}} \left(\Phi,\varphi,\gamma;\mu\right)=\underset{{n}\geqslant\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\Phi\right)_{{n}} \left(\varphi\right)_{{n}} }{{n}!\left(\gamma\right)_{{n}} }\mu^{{n}} \\ $$$$\left(\zeta\right)_{{n}} =\zeta\left(\zeta+\mathrm{1}\right)\left(\zeta+\mathrm{2}\right)...\left(\zeta+{n}−\mathrm{1}\right) \\ $$

Answered by mindispower last updated on 05/Jan/21

=1+Σ_(n≥1) ((Π_(k=0) ^(n−1) (4k+1)^2 )/(16^n (n!)^2 )) =1+Σ_(n≥1) ((4^(2n) .Π_(k=0) ^(n−1) (k+(1/4)).Π(k+(1/4)))/(.16^n .n!)).(1/(n!)) =1+Σ_(n≥1) ((((1/4))_n .((1/4))_n )/((1)_n )).(1^n /(n!))=_2 F_1 ((1/4),(1/4);1;[1]) than use relation _2 F_1 (a,b,c;1) withe β, Γ

$$=\mathrm{1}+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left(\mathrm{4}{k}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{16}^{{n}} \left({n}!\right)^{\mathrm{2}} }\:\: \\ $$$$=\mathrm{1}+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{4}^{\mathrm{2}{n}} .\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left({k}+\frac{\mathrm{1}}{\mathrm{4}}\right).\Pi\left({k}+\frac{\mathrm{1}}{\mathrm{4}}\right)}{.\mathrm{16}^{{n}} .{n}!}.\frac{\mathrm{1}}{{n}!} \\ $$$$=\mathrm{1}+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(\frac{\mathrm{1}}{\mathrm{4}}\right)_{{n}} .\left(\frac{\mathrm{1}}{\mathrm{4}}\right)_{{n}} }{\left(\mathrm{1}\right)_{{n}} }.\frac{\mathrm{1}^{{n}} }{{n}!}=_{\mathrm{2}} {F}_{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{4}},\frac{\mathrm{1}}{\mathrm{4}};\mathrm{1};\left[\mathrm{1}\right]\right) \\ $$$${than}\:{use}\:{relation}\:_{\mathrm{2}} {F}_{\mathrm{1}} \left({a},{b},{c};\mathrm{1}\right)\:{withe}\:\beta, \\ $$$$\Gamma\: \\ $$$$ \\ $$

Commented by Dwaipayan Shikari last updated on 05/Jan/21

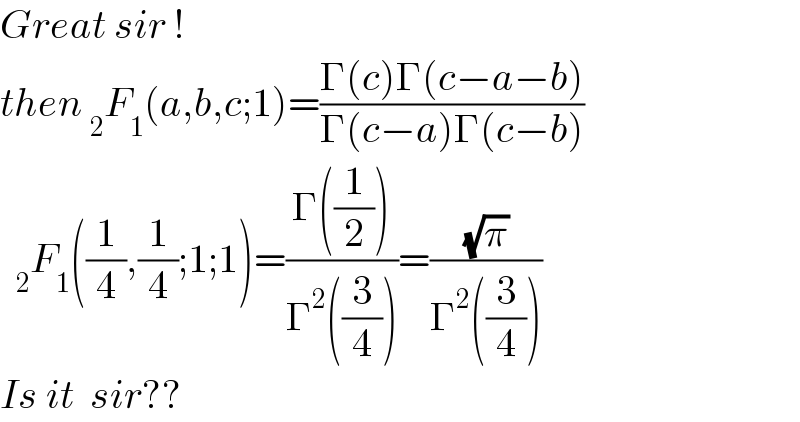
Great sir ! then _2 F_1 (a,b,c;1)=((Γ(c)Γ(c−a−b))/(Γ(c−a)Γ(c−b))) _2 F_1 ((1/4),(1/4);1;1)=((Γ((1/2)))/(Γ^2 ((3/4))))=((√π)/(Γ^2 ((3/4)))) Is it sir??

$${Great}\:{sir}\:! \\ $$$${then}\:_{\mathrm{2}} {F}_{\mathrm{1}} \left({a},{b},{c};\mathrm{1}\right)=\frac{\Gamma\left({c}\right)\Gamma\left({c}−{a}−{b}\right)}{\Gamma\left({c}−{a}\right)\Gamma\left({c}−{b}\right)}\:\: \\ $$$$\:\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{4}},\frac{\mathrm{1}}{\mathrm{4}};\mathrm{1};\mathrm{1}\right)=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)}=\frac{\sqrt{\pi}}{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)} \\ $$$${Is}\:{it}\:\:{sir}?? \\ $$

Commented by mindispower last updated on 06/Jan/21

yes sir great

$${yes}\:{sir}\:{great} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com