
Question and Answers Forum
Question Number 128150 by MJS_new last updated on 04/Jan/21
![question 128091, trying to solve completely in R a^3 =3(b^2 +c^2 )−25 b^3 =3(a^2 +c^2 )−25 c^3 =3(a^2 +b^2 )−25 abc=? (1) a=b=c a^3 −6a^3 +25=0 (a−5)(a^2 −a−5)=0 a=5∨a=(1/2)−((√(21))/2)∨a=(1/2)+((√(21))/2) (2) c=b≠a a^3 =6b^2 −25 ⇒ a=((6b^2 −25))^(1/3) b^3 =3(a^2 +b^2 )−25 b^3 −3b^2 +25=3(6b^2 −25)^(2/3) b^9 −9b^8 +27b^7 +48b^6 −450b^5 −297b^4 +1875b^3 +2475b^2 −1250=0 (b−5)(b^2 −b−5)(b^6 −3b^5 +9b^4 +77b^3 +87b^2 −50)=0 the 1^(st) and 2^(nd) brackets are included in (1) b^6 −3b^5 +9b^4 +77b^3 +87b^2 −50=0 b_1 ≈.605473087 b_2 ≈−2.08139378 a_1 ≈−2.83561704 a_2 ≈.997728331 (3) a≠b≠c let b=pa∧c=qa a^3 =3a^2 (p^2 +q^2 )−25 a^3 p^3 =3a^2 (q^2 +1)−25 a^3 q^3 =3a^2 (p^2 +1)−25 3a^2 (p^2 +q^2 )−25=((3a^2 (q^2 +1)−25)/p^3 ) 3a^2 (p^2 +q^2 )−25=((3a^2 (p^2 +1)−25)/q^3 ) ⇒ [p=1∧q=1 included in (1)∨(2)] a^2 =((25(p^2 +p+1))/(3(p^4 +p^3 +p^2 q^2 +p^2 +pq^2 +p+q^2 +1))) a^2 =((25(q^2 +q+1))/(3(p^2 q^2 +p^2 q+p^2 +q^4 +q^3 +q^2 +q+1))) equating and transforming ⇒ q^2 −(p^2 /(p+1))q−(p^2 /(p+1))=0 q=−(p/(p+1)) [q=p included in (1)∨(2)] ⇒ a^2 =((25(p+1)^2 (p^2 +p+1))/(3(p^6 +3p^5 +5p^4 +5p^3 +5p^2 +3p+1))) inserting above leads to (assuming a<b<c) a=−1−(√3)∧b=−1∧c=−1+(√3) all solutions interchangeable a⇆b⇆c](Q128150.png)
Commented by MJS_new last updated on 04/Jan/21
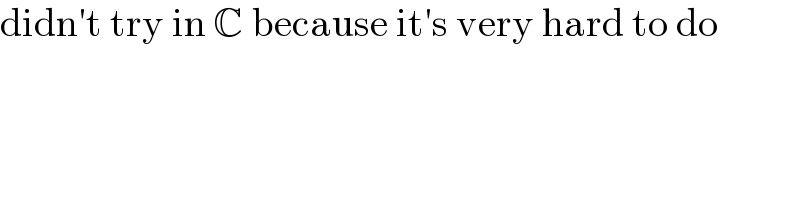
Commented by Tawa11 last updated on 06/Nov/21

Answered by rydasss last updated on 05/Jan/21

| ||
Question and Answers Forum | ||
Question Number 128150 by MJS_new last updated on 04/Jan/21 | ||
![question 128091, trying to solve completely in R a^3 =3(b^2 +c^2 )−25 b^3 =3(a^2 +c^2 )−25 c^3 =3(a^2 +b^2 )−25 abc=? (1) a=b=c a^3 −6a^3 +25=0 (a−5)(a^2 −a−5)=0 a=5∨a=(1/2)−((√(21))/2)∨a=(1/2)+((√(21))/2) (2) c=b≠a a^3 =6b^2 −25 ⇒ a=((6b^2 −25))^(1/3) b^3 =3(a^2 +b^2 )−25 b^3 −3b^2 +25=3(6b^2 −25)^(2/3) b^9 −9b^8 +27b^7 +48b^6 −450b^5 −297b^4 +1875b^3 +2475b^2 −1250=0 (b−5)(b^2 −b−5)(b^6 −3b^5 +9b^4 +77b^3 +87b^2 −50)=0 the 1^(st) and 2^(nd) brackets are included in (1) b^6 −3b^5 +9b^4 +77b^3 +87b^2 −50=0 b_1 ≈.605473087 b_2 ≈−2.08139378 a_1 ≈−2.83561704 a_2 ≈.997728331 (3) a≠b≠c let b=pa∧c=qa a^3 =3a^2 (p^2 +q^2 )−25 a^3 p^3 =3a^2 (q^2 +1)−25 a^3 q^3 =3a^2 (p^2 +1)−25 3a^2 (p^2 +q^2 )−25=((3a^2 (q^2 +1)−25)/p^3 ) 3a^2 (p^2 +q^2 )−25=((3a^2 (p^2 +1)−25)/q^3 ) ⇒ [p=1∧q=1 included in (1)∨(2)] a^2 =((25(p^2 +p+1))/(3(p^4 +p^3 +p^2 q^2 +p^2 +pq^2 +p+q^2 +1))) a^2 =((25(q^2 +q+1))/(3(p^2 q^2 +p^2 q+p^2 +q^4 +q^3 +q^2 +q+1))) equating and transforming ⇒ q^2 −(p^2 /(p+1))q−(p^2 /(p+1))=0 q=−(p/(p+1)) [q=p included in (1)∨(2)] ⇒ a^2 =((25(p+1)^2 (p^2 +p+1))/(3(p^6 +3p^5 +5p^4 +5p^3 +5p^2 +3p+1))) inserting above leads to (assuming a<b<c) a=−1−(√3)∧b=−1∧c=−1+(√3) all solutions interchangeable a⇆b⇆c](Q128150.png) | ||
Commented by MJS_new last updated on 04/Jan/21 | ||
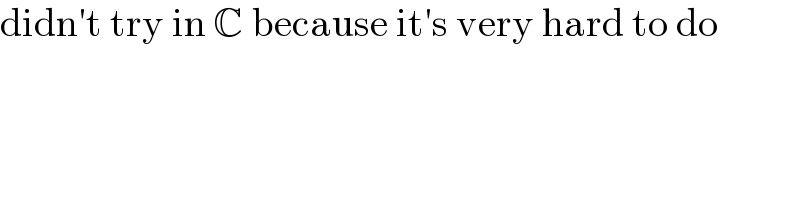 | ||
Commented by Tawa11 last updated on 06/Nov/21 | ||
 | ||
Answered by rydasss last updated on 05/Jan/21 | ||
 | ||
| ||