
Question and Answers Forum
Question Number 128182 by BHOOPENDRA last updated on 05/Jan/21

Commented by BHOOPENDRA last updated on 05/Jan/21
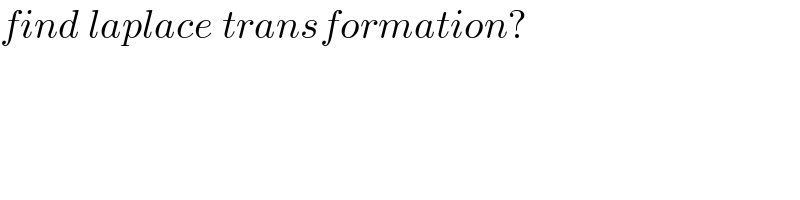
Answered by mathmax by abdo last updated on 05/Jan/21
![2) { ((f(t)=(t−2)^2 if t>2)),((o if t<2 ⇒L(f(t)) =∫_0 ^∞ e^(−tx) (x−2)^2 dx)) :} =∫_2 ^(+∞) (x−2)^2 e^(−tx) dx =[−(1/t)e^(−tx) (x−2)^2 ]_(x=2) ^∞ +2∫_2 ^(+∞) (1/t)e^(−tx) (x−2)dx =(2/t)∫_2 ^(+∞) e^(−tx) (x−2)dx =(2/t){ [−(1/t)e^(−tx) (x−2)]_2 ^∞ +∫_2 ^∞ (1/t)e^(−tx) dx} =(2/t^2 )∫_2 ^(+∞) e^(−tx) dx =(2/t^2 )[−(1/t)e^(−tx) ]_2 ^∞ =(2/t^2 )((e^(−2t) /t)) =((2e^(−2t) )/t^3 )](Q128261.png)
Commented by BHOOPENDRA last updated on 06/Jan/21
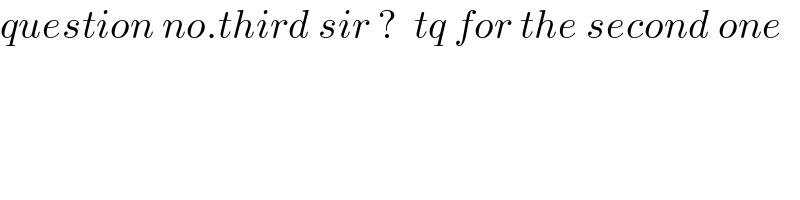
| ||
Question and Answers Forum | ||
Question Number 128182 by BHOOPENDRA last updated on 05/Jan/21 | ||
 | ||
Commented by BHOOPENDRA last updated on 05/Jan/21 | ||
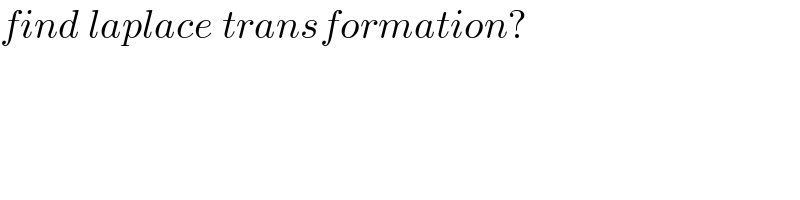 | ||
Answered by mathmax by abdo last updated on 05/Jan/21 | ||
![2) { ((f(t)=(t−2)^2 if t>2)),((o if t<2 ⇒L(f(t)) =∫_0 ^∞ e^(−tx) (x−2)^2 dx)) :} =∫_2 ^(+∞) (x−2)^2 e^(−tx) dx =[−(1/t)e^(−tx) (x−2)^2 ]_(x=2) ^∞ +2∫_2 ^(+∞) (1/t)e^(−tx) (x−2)dx =(2/t)∫_2 ^(+∞) e^(−tx) (x−2)dx =(2/t){ [−(1/t)e^(−tx) (x−2)]_2 ^∞ +∫_2 ^∞ (1/t)e^(−tx) dx} =(2/t^2 )∫_2 ^(+∞) e^(−tx) dx =(2/t^2 )[−(1/t)e^(−tx) ]_2 ^∞ =(2/t^2 )((e^(−2t) /t)) =((2e^(−2t) )/t^3 )](Q128261.png) | ||
| ||
Commented by BHOOPENDRA last updated on 06/Jan/21 | ||
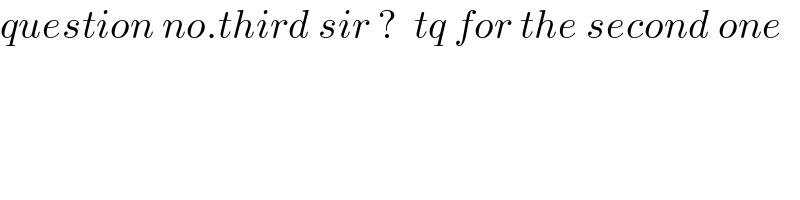 | ||