
Question and Answers Forum
Question Number 128626 by john_santu last updated on 09/Jan/21
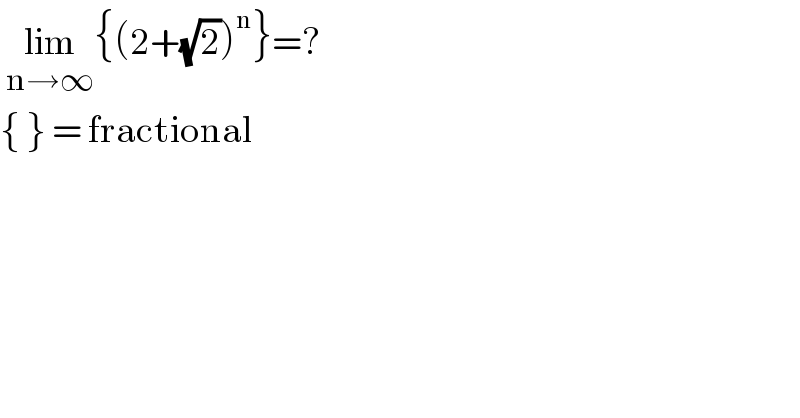
Commented by liberty last updated on 09/Jan/21

Answered by mnjuly1970 last updated on 09/Jan/21
![solution: t_n :=(2+(√2) )^n +(2−(√2) )^n ∈^(why?) N because: t_n =Σ_(k=0) ^n { ((n),(k) ) (2)^(n−k) ((√2) )^k (1+(−1)^k ) =Σ_(k=_(k ∈ N_( E) ) 0) ^n { ((n),(k) ) 2^(n−k+(k/2)+1) } =Σ_(k=_(k∈N_( E) ) 0) { ((n),(k) ) 2^([n+(k/2)+1∈ N]) }∈N b ut we know: 0<( 2−(√2) )^n <1 ∴ 0< 1−(2−(√(2 )) )^n <1 lim_(n→∞ ) (1−(2−(√2) )^n )=1 {(2+(√2) )^n }={t_n −(2−(√2) )^n } ={t_n −1+1−(2−(√2) )^n } ∴lim_(n→∞) {(2+(√2) )^n }=1 note:{t_n −1}=0](Q128658.png)
| ||
Question and Answers Forum | ||
Question Number 128626 by john_santu last updated on 09/Jan/21 | ||
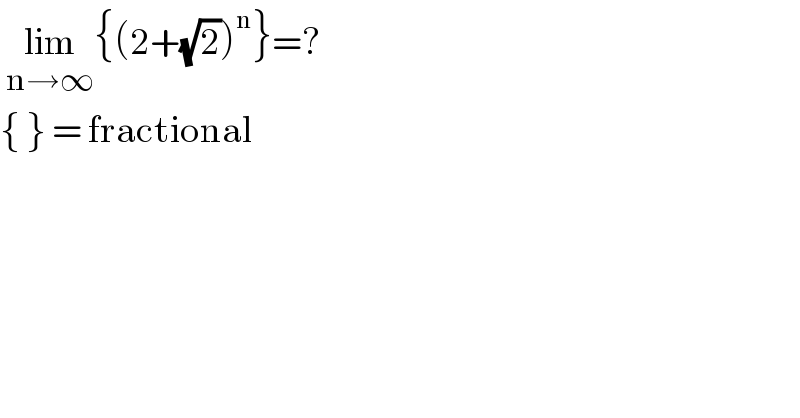 | ||
Commented by liberty last updated on 09/Jan/21 | ||
 | ||
Answered by mnjuly1970 last updated on 09/Jan/21 | ||
![solution: t_n :=(2+(√2) )^n +(2−(√2) )^n ∈^(why?) N because: t_n =Σ_(k=0) ^n { ((n),(k) ) (2)^(n−k) ((√2) )^k (1+(−1)^k ) =Σ_(k=_(k ∈ N_( E) ) 0) ^n { ((n),(k) ) 2^(n−k+(k/2)+1) } =Σ_(k=_(k∈N_( E) ) 0) { ((n),(k) ) 2^([n+(k/2)+1∈ N]) }∈N b ut we know: 0<( 2−(√2) )^n <1 ∴ 0< 1−(2−(√(2 )) )^n <1 lim_(n→∞ ) (1−(2−(√2) )^n )=1 {(2+(√2) )^n }={t_n −(2−(√2) )^n } ={t_n −1+1−(2−(√2) )^n } ∴lim_(n→∞) {(2+(√2) )^n }=1 note:{t_n −1}=0](Q128658.png) | ||
| ||