
Question and Answers Forum
Question Number 128633 by Lordose last updated on 09/Jan/21
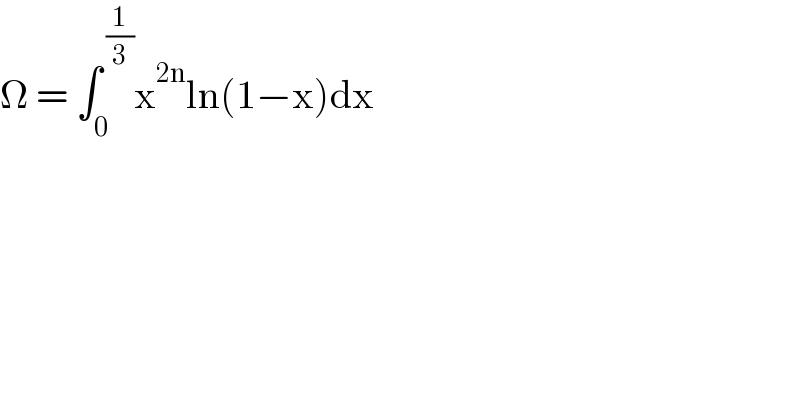
Answered by mathmax by abdo last updated on 09/Jan/21
![let try another way x=(t/3) ⇒ Ω=∫_0 ^1 ((t/3))^(2n) ln(1−(t/3))(dt/3) =(1/3^(2n+1) )∫_0 ^1 t^(2n) ln(((3−t)/3))dt =(1/3^(2n+1) ) ∫_0 ^1 t^(2n) ln(3−t)dt−(1/3^(2n+1) )ln(3)[(t^(2n+1) /(2n+1))]_0 ^1 =(1/3^(2n+1) )∫_0 ^1 t^(2n) ln(3−t)dt −((ln3)/((2n+1)3^(2n+1) )) we have by parts ∫_0 ^1 t^(2n) ln(3−t)dt =[(t^(2n+1) /(2n+1))ln(3−t)]_0 ^1 −∫_0 ^1 (t^(2n+1) /(2n+1))×((−1)/(3−t))dt =(1/(2n+1))ln(2)+(1/(2n+1))∫_0 ^1 (t^(2n+1) /(3−t))dt and ∫_0 ^1 (t^(2n+1) /(3−t)) dt =_(3−t=u) −∫_2 ^3 (((3−u)^(2n+1) )/u)(−du) =−∫_2 ^3 (((u−3)^(2n+1) )/u) du =−∫_2 ^3 ((Σ_(k=0) ^(2n+1) C_(2n+1) ^k u^k (−3)^(2n+1−k) )/u)du =3^(2n+1) Σ_(k=1) ^(2n+1) (−3)^(−k) C_(2n+1) ^k ∫_2 ^3 u^(k−1) du −3^(2n+1) ln((3/2)) =3^(2n+1) Σ_(k=0) ^(2n+1) (−3)^(−k) C_(2n+1) ^k (1/k){ 3^(k−1) −2^(k−1) }−3^(2n+1) ln((3/2))...](Q128705.png)
Answered by mathmax by abdo last updated on 09/Jan/21
![Ω=∫_0 ^(1/3) x^(2n) ln(1−x)dx by parts u^′ =x^(2n) [and v=ln(1−x) Ω=[(x^(2n+1) /(2n+1))ln(1−x)]_0 ^(1/3) −∫_0 ^(1/3) (x^(2n+1) /(2n+1))×((−1)/(1−x))dx =(1/(2n+1(3)^(2n+1) ))ln((2/3))+(1/(2n+1))∫_0 ^(1/3) (x^(2n+1) /(1−x))dx but ∫_0 ^(1/3) (x^(2n+1) /(1−x))dx =∫_0 ^(1/3) ((x^(2n+1) −1+1)/(1−x))dx =∫_0 ^(1/3) (((x−1)(1+x+x^2 +...+x^(2n) ))/(1−x))dx +[−ln(1−x)]_0 ^(1/3) =−∫_0 ^(1/3) (Σ_(k=0) ^(2n) x^k )dx−ln((2/3)) =−Σ_(k=0) ^(2n) [(x^(k+1) /(k+1))]_0 ^(1/3) −ln2 +ln3 =−Σ_(k=0) ^(2n) (1/((k+1)3^(k+1) )) +ln3−ln2 rsst to find the value of this serie...](Q128703.png)
| ||
Question and Answers Forum | ||
Question Number 128633 by Lordose last updated on 09/Jan/21 | ||
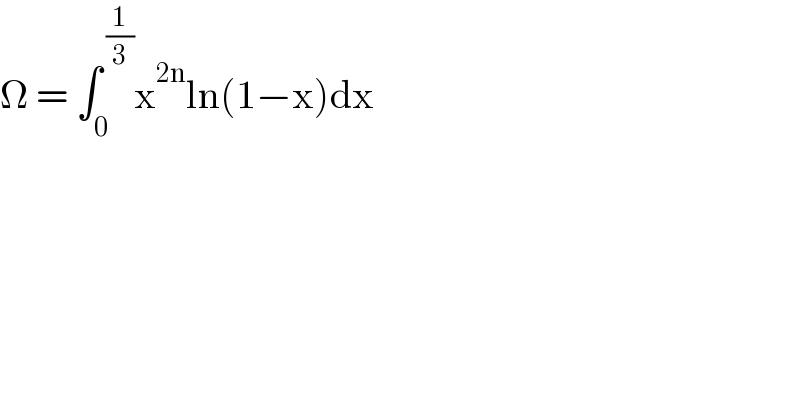 | ||
Answered by mathmax by abdo last updated on 09/Jan/21 | ||
![let try another way x=(t/3) ⇒ Ω=∫_0 ^1 ((t/3))^(2n) ln(1−(t/3))(dt/3) =(1/3^(2n+1) )∫_0 ^1 t^(2n) ln(((3−t)/3))dt =(1/3^(2n+1) ) ∫_0 ^1 t^(2n) ln(3−t)dt−(1/3^(2n+1) )ln(3)[(t^(2n+1) /(2n+1))]_0 ^1 =(1/3^(2n+1) )∫_0 ^1 t^(2n) ln(3−t)dt −((ln3)/((2n+1)3^(2n+1) )) we have by parts ∫_0 ^1 t^(2n) ln(3−t)dt =[(t^(2n+1) /(2n+1))ln(3−t)]_0 ^1 −∫_0 ^1 (t^(2n+1) /(2n+1))×((−1)/(3−t))dt =(1/(2n+1))ln(2)+(1/(2n+1))∫_0 ^1 (t^(2n+1) /(3−t))dt and ∫_0 ^1 (t^(2n+1) /(3−t)) dt =_(3−t=u) −∫_2 ^3 (((3−u)^(2n+1) )/u)(−du) =−∫_2 ^3 (((u−3)^(2n+1) )/u) du =−∫_2 ^3 ((Σ_(k=0) ^(2n+1) C_(2n+1) ^k u^k (−3)^(2n+1−k) )/u)du =3^(2n+1) Σ_(k=1) ^(2n+1) (−3)^(−k) C_(2n+1) ^k ∫_2 ^3 u^(k−1) du −3^(2n+1) ln((3/2)) =3^(2n+1) Σ_(k=0) ^(2n+1) (−3)^(−k) C_(2n+1) ^k (1/k){ 3^(k−1) −2^(k−1) }−3^(2n+1) ln((3/2))...](Q128705.png) | ||
| ||
Answered by mathmax by abdo last updated on 09/Jan/21 | ||
![Ω=∫_0 ^(1/3) x^(2n) ln(1−x)dx by parts u^′ =x^(2n) [and v=ln(1−x) Ω=[(x^(2n+1) /(2n+1))ln(1−x)]_0 ^(1/3) −∫_0 ^(1/3) (x^(2n+1) /(2n+1))×((−1)/(1−x))dx =(1/(2n+1(3)^(2n+1) ))ln((2/3))+(1/(2n+1))∫_0 ^(1/3) (x^(2n+1) /(1−x))dx but ∫_0 ^(1/3) (x^(2n+1) /(1−x))dx =∫_0 ^(1/3) ((x^(2n+1) −1+1)/(1−x))dx =∫_0 ^(1/3) (((x−1)(1+x+x^2 +...+x^(2n) ))/(1−x))dx +[−ln(1−x)]_0 ^(1/3) =−∫_0 ^(1/3) (Σ_(k=0) ^(2n) x^k )dx−ln((2/3)) =−Σ_(k=0) ^(2n) [(x^(k+1) /(k+1))]_0 ^(1/3) −ln2 +ln3 =−Σ_(k=0) ^(2n) (1/((k+1)3^(k+1) )) +ln3−ln2 rsst to find the value of this serie...](Q128703.png) | ||
| ||