Question and Answers Forum
Question Number 12883 by FilupS last updated on 05/May/17

Answered by mrW1 last updated on 10/May/17
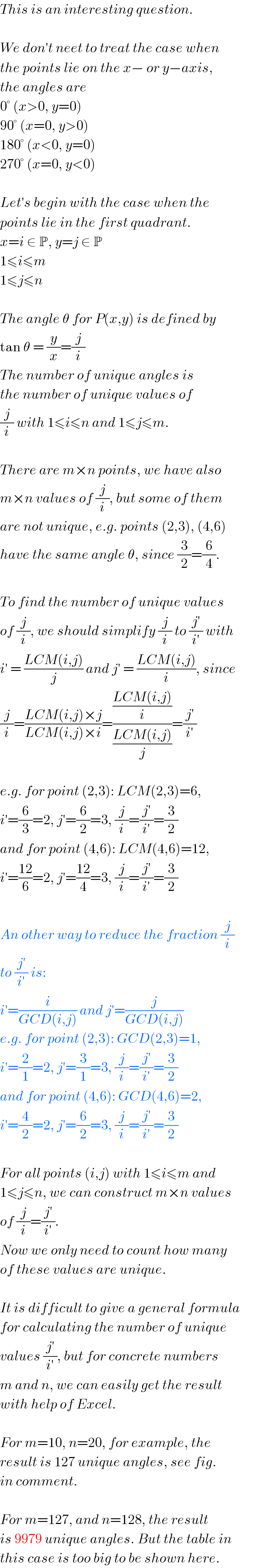
Commented by mrW1 last updated on 07/May/17
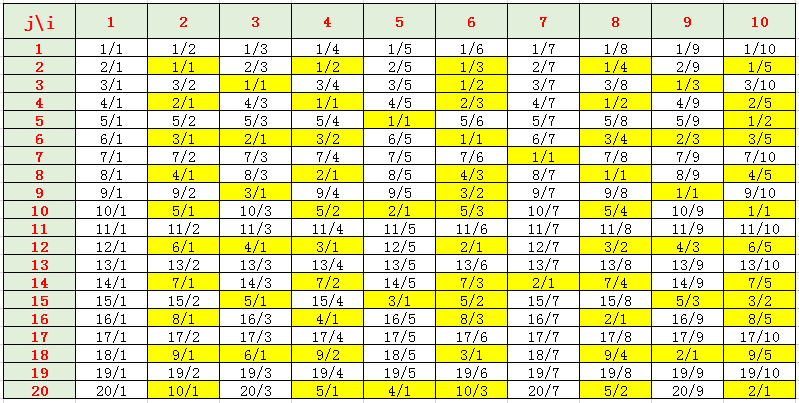
Commented by mrW1 last updated on 07/May/17
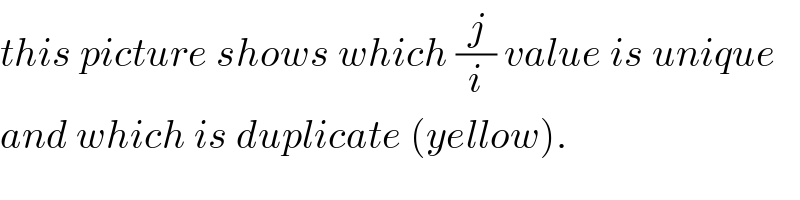
Commented by FilupS last updated on 07/May/17
Commented by mrW1 last updated on 11/May/17
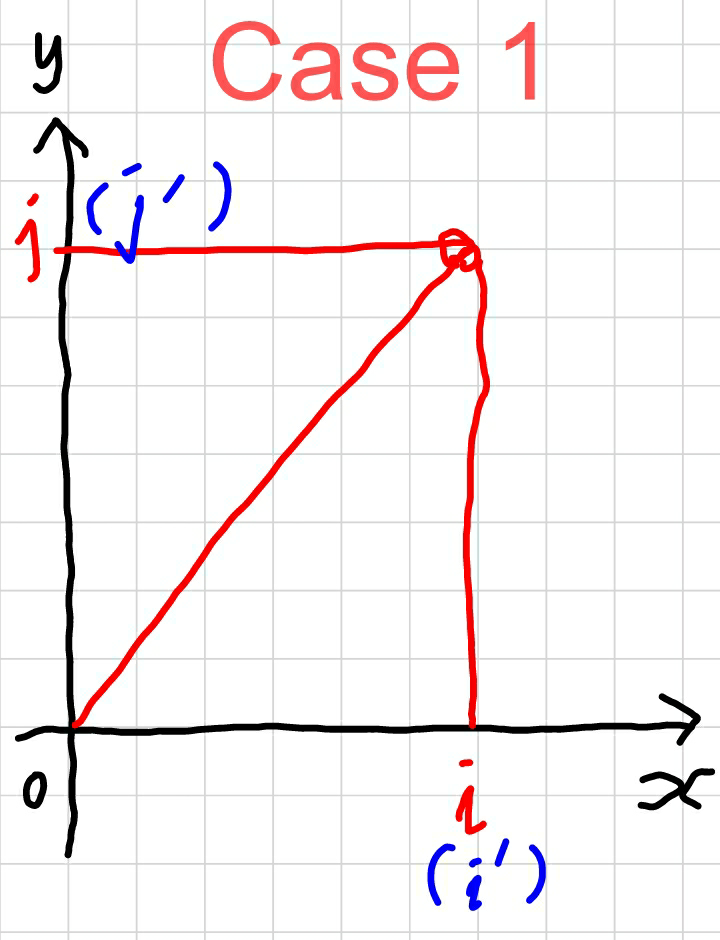
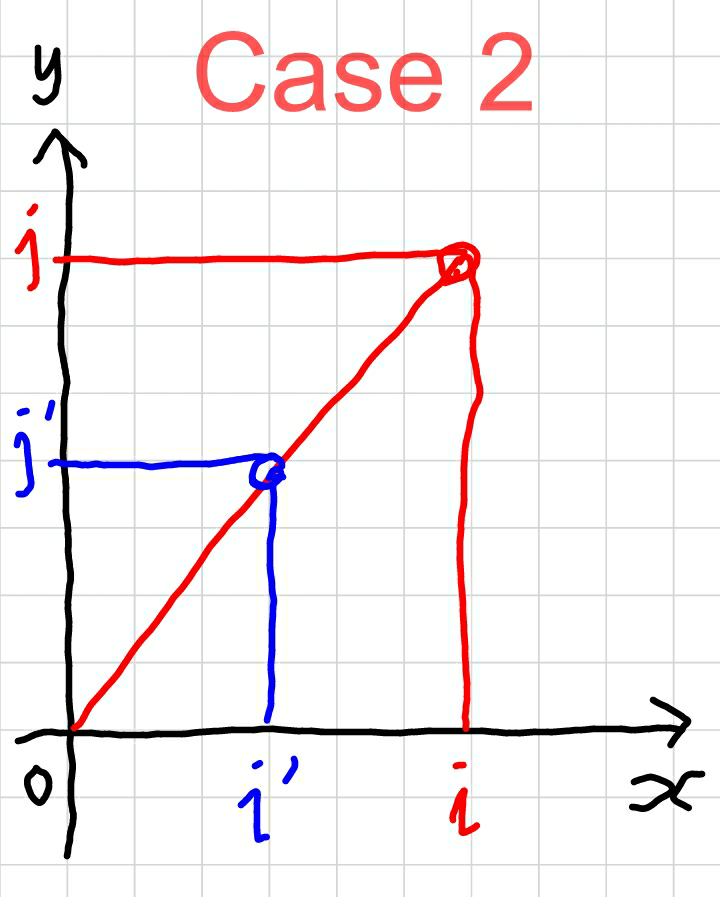
![Here the explanation how it works. We have: (j/i)=((j′)/(i′)) with i′=((LCM(i,j))/j) [or (i/(GCD(i,j)))] j′=((LCM(i,j))/i) [or (j/(GCD(i,j)))] For each point (i,j) it can be one of following two cases: Case 1: i′=i and j′=j ⇒point (i,j) descripts a new angle. e.g. point (2,7): LCM(2,7)=14 i′=((14)/7)=2=i j′=((14)/2)=7=j ⇒point (2,7) has a new angle. Case 2: i′<i and j′<j ⇒point (i,j) descripts no new angle, its angle is the same as for point(i′,j′). e.g. point (8,20): LCM(8,20)=40 i′=((40)/(20))=2<i=8 j′=((40)/8)=5<j=20 ⇒point (8,20) has no new angle, since it has the same angle as point (2,5). Case 1 means also GCD(i,j)=1. Case 2 means also GCD(i,j)>1.](Q12971.png)
Commented by mrW1 last updated on 08/May/17
Commented by mrW1 last updated on 08/May/17
Commented by mrW1 last updated on 09/May/17

Commented by mrW1 last updated on 08/May/17
Commented by mrW1 last updated on 09/May/17

Commented by mrW1 last updated on 09/May/17
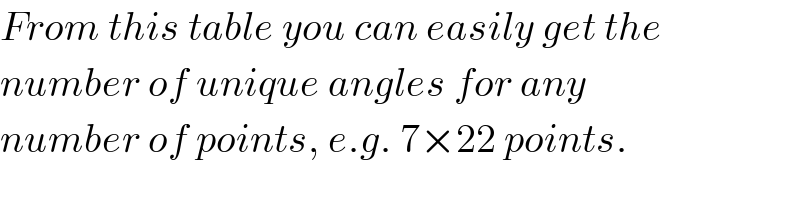
Commented by mrW1 last updated on 09/May/17
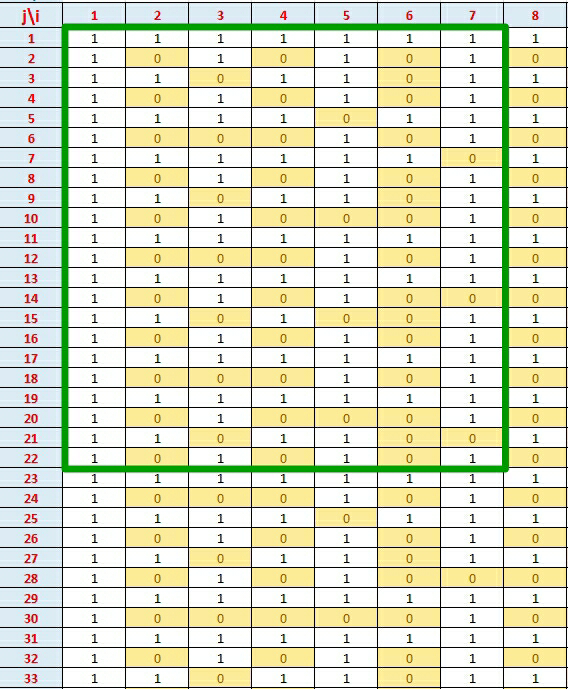
Commented by mrW1 last updated on 09/May/17

Commented by FilupS last updated on 09/May/17
Commented by FilupS last updated on 09/May/17

Commented by FilupS last updated on 09/May/17

Commented by mrW1 last updated on 09/May/17
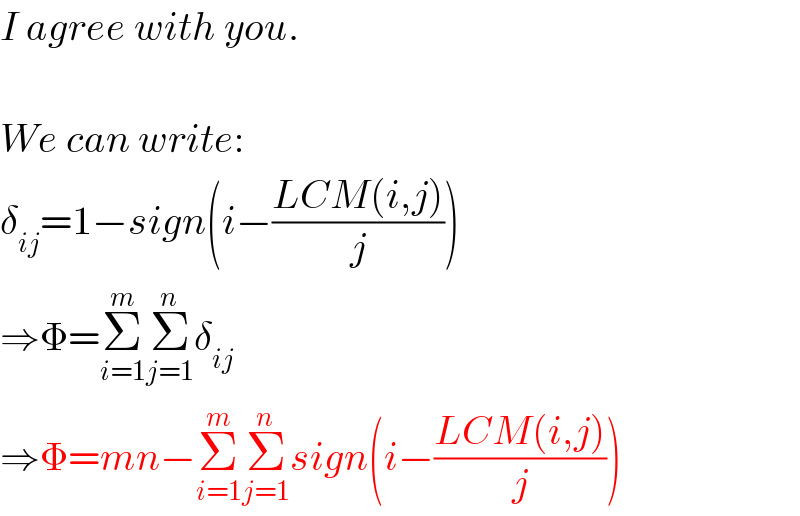
Commented by FilupS last updated on 09/May/17

Commented by mrW1 last updated on 09/May/17
Commented by FilupS last updated on 09/May/17
Commented by mrW1 last updated on 10/May/17

Commented by mrW1 last updated on 10/May/17

Commented by FilupS last updated on 10/May/17