
Question and Answers Forum
Question Number 128846 by Ar Brandon last updated on 10/Jan/21
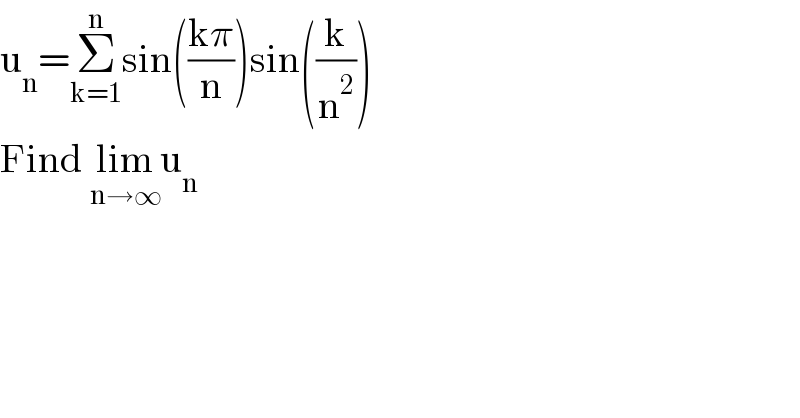
Commented by Dwaipayan Shikari last updated on 10/Jan/21
![lim_(n→∞) sin((k/n^2 ))=(k/n^2 ) u_n =lim_(n→∞) (1/n)Σ_(k=1) ^n (k/n)sin((kπ)/n) =∫_0 ^1 xsinxπ dx = (1/π^2 )∫_0 ^π u sinu =(1/π^2 )[−u cosu]_0 ^π +(1/π^2 )∫_0 ^π cosu du =(1/π)](Q128847.png)
Commented by Dwaipayan Shikari last updated on 10/Jan/21
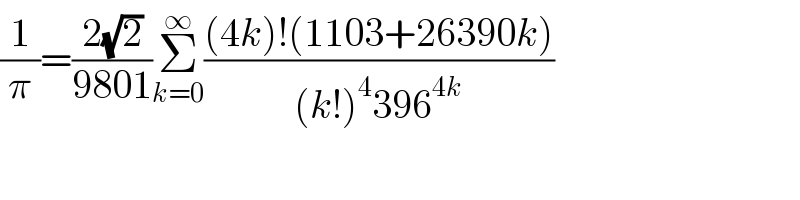
| ||
Question and Answers Forum | ||
Question Number 128846 by Ar Brandon last updated on 10/Jan/21 | ||
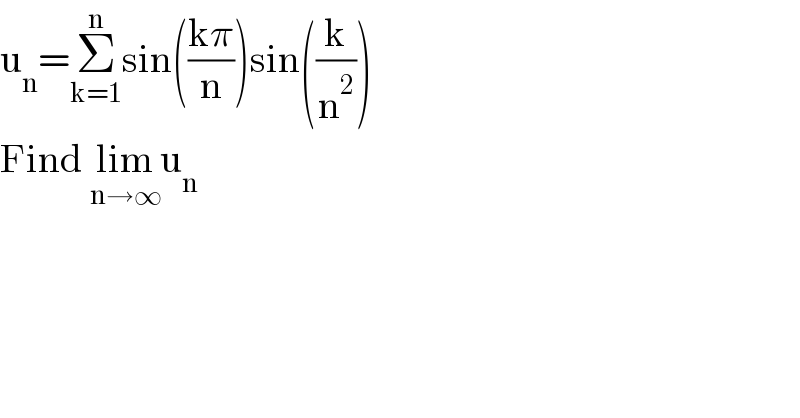 | ||
Commented by Dwaipayan Shikari last updated on 10/Jan/21 | ||
![lim_(n→∞) sin((k/n^2 ))=(k/n^2 ) u_n =lim_(n→∞) (1/n)Σ_(k=1) ^n (k/n)sin((kπ)/n) =∫_0 ^1 xsinxπ dx = (1/π^2 )∫_0 ^π u sinu =(1/π^2 )[−u cosu]_0 ^π +(1/π^2 )∫_0 ^π cosu du =(1/π)](Q128847.png) | ||
Commented by Dwaipayan Shikari last updated on 10/Jan/21 | ||
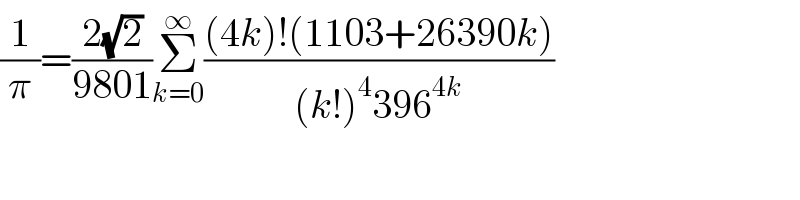 | ||