Question Number 128851 by mnjuly1970 last updated on 10/Jan/21
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:...{nice}\:\:\:{calculus}\:\:\left({I}\right)... \\ $$$$\:\:\:{calculate}\:\::: \\ $$$$ \\ $$$$\:\:\:\:\:\Psi=\int_{\mathrm{0}} ^{\:\mathrm{1}} \left\{\left({e}−\mathrm{1}\right)\sqrt{{log}\left(\:\mathrm{1}+{ex}−{x}\:\right)}\:+{e}^{{x}^{\mathrm{2}} } \right\}{dx}=? \\ $$$$ \\ $$
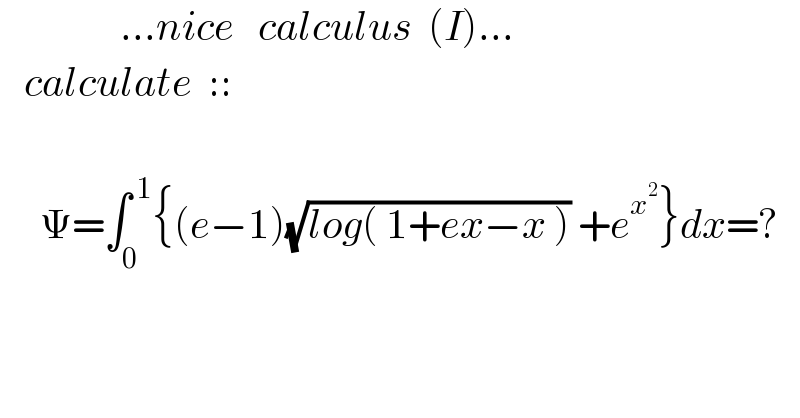
Commented by mindispower last updated on 10/Jan/21
$$\left\{.\right\}\:{fraction}\:{part}\:? \\ $$
Commented by mnjuly1970 last updated on 11/Jan/21
$${no}\:{mr}\:{power} \\ $$
Answered by Olaf last updated on 11/Jan/21
![Let f(x) = (e−1)(√(ln(1+(e−1)x))+e^x^2 f is clearly an increasing function and f(0) = 1, f(1) = e ⇒ ∃a∈]0,1[ \ f(a) = 2 Ψ = ∫_0 ^1 {f(x)}dx = ∫_0 ^a {f(x)}dx+∫_a ^1 {f(x)}dx Ψ = ∫_0 ^a (f(x)−1)dx+∫_a ^1 (f(x)−2)dx Ψ = ∫_0 ^1 f(x)dx−a−2(1−a) Ψ = ∫_0 ^1 f(x)dx+a−2 Let u = ln(1+(e−1)x) e^u = 1+(e−1)x e^u du = (e−1)dx I = (e−1)∫_0 ^1 (√(ln(1+(e−1)x)))dx I = (e−1)∫_0 ^1 (√u)((e^u du)/(e−1)) I = ∫_0 ^1 (√u)e^u du I = [(√x)e^x −((√π)/2)erfi((√x))]_0 ^1 = e−((√π)/2)erfi(1) J = ∫_0 ^1 e^x^2 dx = [((√π)/2)erfi(x)]_0 ^1 = ((√π)/2)erfi(1) Ψ = I+J+a−2 = e+a−2 (a ≈ 0,542)](Q128875.png)
$$\mathrm{Let}\:{f}\left({x}\right)\:=\:\left({e}−\mathrm{1}\right)\sqrt{\mathrm{ln}\left(\mathrm{1}+\left({e}−\mathrm{1}\right){x}\right.}+{e}^{{x}^{\mathrm{2}} } \\ $$$${f}\:\mathrm{is}\:\mathrm{clearly}\:\mathrm{an}\:\mathrm{increasing}\:\mathrm{function}\:\mathrm{and} \\ $$$${f}\left(\mathrm{0}\right)\:=\:\mathrm{1},\:{f}\left(\mathrm{1}\right)\:=\:{e} \\ $$$$\left.\Rightarrow\:\exists{a}\in\right]\mathrm{0},\mathrm{1}\left[\:\backslash\:{f}\left({a}\right)\:=\:\mathrm{2}\right. \\ $$$$ \\ $$$$\Psi\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \left\{{f}\left({x}\right)\right\}{dx}\:=\:\int_{\mathrm{0}} ^{{a}} \left\{{f}\left({x}\right)\right\}{dx}+\int_{{a}} ^{\mathrm{1}} \left\{{f}\left({x}\right)\right\}{dx} \\ $$$$\Psi\:=\:\int_{\mathrm{0}} ^{{a}} \left({f}\left({x}\right)−\mathrm{1}\right){dx}+\int_{{a}} ^{\mathrm{1}} \left({f}\left({x}\right)−\mathrm{2}\right){dx} \\ $$$$\Psi\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}−{a}−\mathrm{2}\left(\mathrm{1}−{a}\right) \\ $$$$\Psi\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}+{a}−\mathrm{2} \\ $$$$\mathrm{Let}\:{u}\:=\:\mathrm{ln}\left(\mathrm{1}+\left({e}−\mathrm{1}\right){x}\right) \\ $$$${e}^{{u}} \:=\:\mathrm{1}+\left({e}−\mathrm{1}\right){x} \\ $$$${e}^{{u}} {du}\:=\:\left({e}−\mathrm{1}\right){dx} \\ $$$$ \\ $$$$\mathrm{I}\:=\:\left({e}−\mathrm{1}\right)\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{ln}\left(\mathrm{1}+\left({e}−\mathrm{1}\right){x}\right)}{dx} \\ $$$$\mathrm{I}\:=\:\left({e}−\mathrm{1}\right)\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{u}}\frac{{e}^{{u}} {du}}{{e}−\mathrm{1}} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{u}}{e}^{{u}} {du} \\ $$$$\mathrm{I}\:=\:\left[\sqrt{{x}}{e}^{{x}} −\frac{\sqrt{\pi}}{\mathrm{2}}\mathrm{erfi}\left(\sqrt{{x}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\:{e}−\frac{\sqrt{\pi}}{\mathrm{2}}\mathrm{erfi}\left(\mathrm{1}\right) \\ $$$$ \\ $$$$\mathrm{J}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{x}^{\mathrm{2}} } {dx}\:=\:\left[\frac{\sqrt{\pi}}{\mathrm{2}}\mathrm{erfi}\left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\:\frac{\sqrt{\pi}}{\mathrm{2}}\mathrm{erfi}\left(\mathrm{1}\right) \\ $$$$ \\ $$$$\Psi\:=\:\mathrm{I}+\mathrm{J}+{a}−\mathrm{2}\:=\:{e}+{a}−\mathrm{2} \\ $$$$\left({a}\:\approx\:\mathrm{0},\mathrm{542}\right) \\ $$
Commented by mnjuly1970 last updated on 11/Jan/21
$${grateful}\:{for}\:{your}\:{work}\:{mr}\:{olaf}.. \\ $$
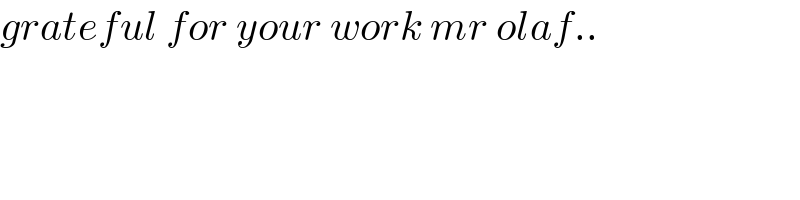
Answered by mnjuly1970 last updated on 11/Jan/21
![note: ∫_(a ) ^( b) f(x)dx+∫_c ^( d) f^( −1) (x)dx=bd−ac Ψ=∫_0 ^( 1) (e−1)(√(log(1+x(e−1))) dx + ∫_0 ^( 1) e^x^2 dx ∴ Ψ=^([u=(1+x(e−1)]) ∫_1 ^( e) (√(log(u))) du+∫_0 ^( 1) e^x^2 dx =∫_1 ^( e) (√(log(x))) +∫_0 ^( 1) e^x^2 dx=e note: f(x)=(√(log(x))) ⇔ f^( −1) (x)=e^x^2](Q128909.png)
$$\:\:\:{note}:\:\int_{{a}\:} ^{\:{b}} {f}\left({x}\right){dx}+\int_{{c}} ^{\:{d}} {f}^{\:−\mathrm{1}} \left({x}\right){dx}={bd}−{ac} \\ $$$$\:\:\Psi=\int_{\mathrm{0}} ^{\:\mathrm{1}} \left({e}−\mathrm{1}\right)\sqrt{{log}\left(\mathrm{1}+{x}\left({e}−\mathrm{1}\right)\right.}\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:+\:\int_{\mathrm{0}} ^{\:\mathrm{1}} {e}^{{x}^{\mathrm{2}} } {dx} \\ $$$$\:\:\therefore\:\Psi\overset{\left[{u}=\left(\mathrm{1}+{x}\left({e}−\mathrm{1}\right)\right]\right.} {=}\int_{\mathrm{1}} ^{\:{e}} \sqrt{{log}\left({u}\right)}\:{du}+\int_{\mathrm{0}} ^{\:\mathrm{1}} {e}^{{x}^{\mathrm{2}} } {dx} \\ $$$$\:\:\:\:\:\:\:\:\:=\int_{\mathrm{1}} ^{\:{e}} \sqrt{{log}\left({x}\right)}\:+\int_{\mathrm{0}} ^{\:\mathrm{1}} {e}^{{x}^{\mathrm{2}} } {dx}={e} \\ $$$$\:\:\:\:{note}:\:{f}\left({x}\right)=\sqrt{{log}\left({x}\right)}\:\Leftrightarrow\:{f}^{\:−\mathrm{1}} \left({x}\right)={e}^{{x}^{\mathrm{2}} } \\ $$
Answered by mnjuly1970 last updated on 11/Jan/21
