calculate A_n =∫_0 ^∞ (dx/((x^2 +1)^n )) , n integr and n≥1


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 128952 by mathmax by abdo last updated on 11/Jan/21

$calculate A_{n} = \int_{0}^{\infty} \frac{dx}{{(x^{2} + 1)}^{n}}, n integr and n ⩾ 1$
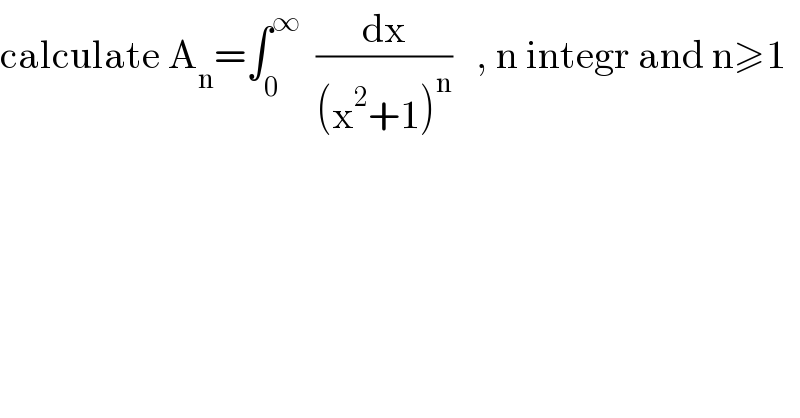
	Answered by Dwaipayan Shikari last updated on 11/Jan/21

	$\int_{0}^{\infty} \frac{d x}{{(x^{2} + 1)}^{n}}$ $= \frac{1}{2} \int_{0}^{\infty} \frac{t^{\frac{1}{2} - 1}}{{(t + 1)}^{(n - \frac{1}{2}) + \frac{1}{2}}} d t = β (\frac{1}{2}, n - \frac{1}{2}) = \frac{Γ (n - \frac{1}{2}) Γ (\frac{1}{2})}{2 Γ (n)}$
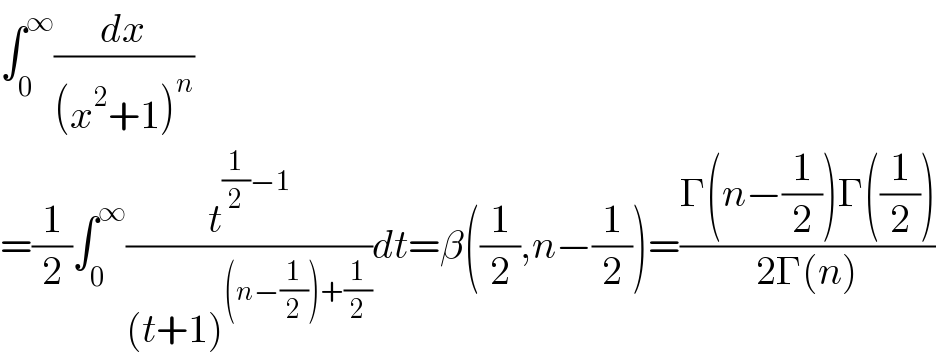
	Answered by mathmax by abdo last updated on 11/Jan/21
	$A_n =∫_0 ^∞ ((x^2 +1)/((x^2 +1)^(n+1) ))dx =∫_0 ^∞ (x^2 /((x^2 +1)^(n+1) ))dx +A_(n+1) we have ∫_0 ^∞ (x^2 /((x^2 +1)^(n+1) ))dx =∫_0 ^∞ x(x(x^2 +1)^(−n−1) )dx by parts u=x and v^′ =x(x^2 +1)^(−n−1) ⇒v=−(1/(2n))(x^2 +1)^(−n) ⇒∫_0 ^∞ ((x^2 dx)/((x^2 +1)^(n+1) )) =[−(x/(2n))(x^2 +1)^(−n) ]_0 ^∞ +(1/(2n))∫_0 ^∞ (dx/((x^2 +1)^n )) =(1/(2n))A_n ⇒A_n =(1/(2n))A_n +A_(n+1) ⇒A_(n+1) =(1−(1/(2n)))A_n ⇒ A_(n+1) =((2n−1)/(2n))A_n ⇒(A_(n+1) /A_n ) =((2n−1)/(2n)) ⇒Π_(k=1) ^(n−1) (A_(k+1) /A_k )=Π_(k=1) ^(n−1) ((2k−1)/(2k)) ⇒ (A_2 /A_1 ).(A_3 /A_2 ).....(A_n /A_(n−1) ) =((Π_(k=1) ^(n−1) (2k−1))/(2^(n−1) (n−1)!))⇒ A_n =A_1 ×((1.3....(2n−3))/(2^(n−1) (n−1)!)) =A_1 ×((1.2.3.....(2n−4)(2n−3)(2n−2))/((2^(n−1) )^2 (n−1)!^2 )) =(((2n−2)!)/(2^(2n−2) ((n−1)!)^2 ))A_1 =(((2n−2)!)/(2^(2n−2) (n−1)!^2 )).(π/2) (n>1) ⇒ A_n =π×(((2n−2)!)/(2^(2n−1) {(n−1)!^2 }))$
	$A_{n} = \int_{0}^{\infty} \frac{x^{2} + 1}{{(x^{2} + 1)}^{n + 1}} dx = \int_{0}^{\infty} \frac{x^{2}}{{(x^{2} + 1)}^{n + 1}} dx + A_{n + 1} we have$ $\int_{0}^{\infty} \frac{x^{2}}{{(x^{2} + 1)}^{n + 1}} dx = \int_{0}^{\infty} x (x {(x^{2} + 1)}^{- n - 1}) dx by parts u = x and$ $v^{^{'}} = x {(x^{2} + 1)}^{- n - 1} \Rightarrow v = - \frac{1}{2 n} {(x^{2} + 1)}^{- n}$ $\Rightarrow \int_{0}^{\infty} \frac{x^{2} dx}{{(x^{2} + 1)}^{n + 1}} = {[- \frac{x}{2 n} {(x^{2} + 1)}^{- n}]}_{0}^{\infty} + \frac{1}{2 n} \int_{0}^{\infty} \frac{dx}{{(x^{2} + 1)}^{n}}$ $= \frac{1}{2 n} A_{n} \Rightarrow A_{n} = \frac{1}{2 n} A_{n} + A_{n + 1} \Rightarrow A_{n + 1} = (1 - \frac{1}{2 n}) A_{n} \Rightarrow$ $A_{n + 1} = \frac{2 n - 1}{2 n} A_{n} \Rightarrow \frac{A_{n + 1}}{A_{n}} = \frac{2 n - 1}{2 n} \Rightarrow \prod_{k = 1}^{n - 1} \frac{A_{k + 1}}{A_{k}} = \prod_{k = 1}^{n - 1} \frac{2 k - 1}{2 k}$ $\Rightarrow \frac{A_{2}}{A_{1}} . \frac{A_{3}}{A_{2}} . . . . . \frac{A_{n}}{A_{n - 1}} = \frac{\prod_{k = 1}^{n - 1} (2 k - 1)}{2^{n - 1} (n - 1)!} \Rightarrow$ $A_{n} = A_{1} \times \frac{1.3 . . . . (2 n - 3)}{2^{n - 1} (n - 1)!} = A_{1} \times \frac{1.2.3 . . . . . (2 n - 4) (2 n - 3) (2 n - 2)}{{(2^{n - 1})}^{2} (n - 1)!^{2}}$ $= \frac{(2 n - 2)!}{2^{2 n - 2} {((n - 1)!)}^{2}} A_{1} = \frac{(2 n - 2)!}{2^{2 n - 2} (n - 1)!^{2}} . \frac{π}{2} (n > 1) \Rightarrow$ $A_{n} = π \times \frac{(2 n - 2)!}{2^{2 n - 1} {(n - 1)!^{2}}}$
	Answered by mathmax by abdo last updated on 11/Jan/21
	$residus method A_n =(1/2)∫_(−∞) ^(+∞) (dx/((x^2 +1)^n )) let ϕ(z)=(1/((z^2 +1)^n )) ⇒ ϕ(z)=(1/((z−i)^n (z+i)^n )) residus give ∫_R ϕ(z)dz=2iπRes(ϕ,i) Res(ϕ,i)=lim_(z→i) (1/((n−1)!)){(z−i)^n ϕ(z)}^((n−1)) =lim_(z→i) (1/((n−1)!)){(z+i)^(−n) }^((n−1)) that lead to find (z+i)^(−n) }^((p)) {(z+i)^(−n) }^((1)) =−n(z+i)^(−n−1) {(z+i)^(−n) }^((2)) =(−1)^2 n(n+1)(z+i)^(−(n+2)) {(z+i)^(−n) }^((p)) =(−1)^p n(n+1)....(n+p−1)(z+i)^(−n−p) p=n−1 ⇒{(z+i)^(−n) }^((n−1)) =(−1)^(n−1) n(n+1)....(n+n−1−1)(z+i)^(−n−(n−1)) =(−1)^(n−1) n(n+1).....(2n−2)(z+i)^(−2n+1) =(((−1)^(n−1) n(n+1)....(2n−2))/((z+i)^(2n−1) )) ⇒ Res(ϕ,i)=lim_(z→i) (1/((n−1)!))×(((−1)^(n−1) n(n+1)....(2n−2))/((z+i)^(2n−1) )) =(((−1)^(n−1) n(n+1)....(2n−2))/((n−1)!(2i)^(2n−1) )) =i(((−1)^(n−1) n(n+1)....(2n−2))/((n−1)!2^(2n−1) (−1)^n )) =−i((n(n+1)....(2n−2))/(2^(2n−1) (n−1)!)) ⇒∫_R ϕ(z)dz =2iπ×(−i)×((n(n+1)....(2n−2))/(2^(2n−1) (n−1)!)) =π×((n(n+1)(n+2)...(2n−2))/(2^(2n−2) (n−1)!))=2A_n ⇒ A_n =(π/2)×((n(n+1)(n+2)....(2n−2))/(2^(2n−2) (n−1)!))$
	$residus method A_{n} = \frac{1}{2} \int_{- \infty}^{+ \infty} \frac{dx}{{(x^{2} + 1)}^{n}} let φ (z) = \frac{1}{{(z^{2} + 1)}^{n}} \Rightarrow$ $φ (z) = \frac{1}{{(z - i)}^{n} {(z + i)}^{n}} residus give \int_{R} φ (z) dz = 2 i π Res (φ, i)$ $Res (φ, i) = \lim_{z \to i} \frac{1}{(n - 1)!} {{(z - i)}^{n} φ (z)}^{(n - 1)} = \lim_{z \to i} \frac{1}{(n - 1)!} {{(z + i)}^{- n}}^{(n - 1)}$ ${that lead to find {(z + i)}^{- n}}}^{(p)}$ ${{(z + i)}^{- n}}^{(1)} = - n {(z + i)}^{- n - 1}$ ${{(z + i)}^{- n}}^{(2)} = {(- 1)}^{2} n (n + 1) {(z + i)}^{- (n + 2)}$ ${{(z + i)}^{- n}}^{(p)} = {(- 1)}^{p} n (n + 1) . . . . (n + p - 1) {(z + i)}^{- n - p}$ $p = n - 1 \Rightarrow {{(z + i)}^{- n}}^{(n - 1)} = {(- 1)}^{n - 1} n (n + 1) . . . . (n + n - 1 - 1) {(z + i)}^{- n - (n - 1)}$ $= {(- 1)}^{n - 1} n (n + 1) . . . . . (2 n - 2) {(z + i)}^{- 2 n + 1}$ $= \frac{{(- 1)}^{n - 1} n (n + 1) . . . . (2 n - 2)}{{(z + i)}^{2 n - 1}} \Rightarrow$ $Res (φ, i) = \lim_{z \to i} \frac{1}{(n - 1)!} \times \frac{{(- 1)}^{n - 1} n (n + 1) . . . . (2 n - 2)}{{(z + i)}^{2 n - 1}}$ $= \frac{{(- 1)}^{n - 1} n (n + 1) . . . . (2 n - 2)}{(n - 1)! {(2 i)}^{2 n - 1}} = i \frac{{(- 1)}^{n - 1} n (n + 1) . . . . (2 n - 2)}{(n - 1)! 2^{2 n - 1} {(- 1)}^{n}}$ $= - i \frac{n (n + 1) . . . . (2 n - 2)}{2^{2 n - 1} (n - 1)!} \Rightarrow \int_{R} φ (z) dz = 2 i π \times (- i) \times \frac{n (n + 1) . . . . (2 n - 2)}{2^{2 n - 1} (n - 1)!}$ $= π \times \frac{n (n + 1) (n + 2) . . . (2 n - 2)}{2^{2 n - 2} (n - 1)!} = {2 A}_{n} \Rightarrow$ $A_{n} = \frac{π}{2} \times \frac{n (n + 1) (n + 2) . . . . (2 n - 2)}{2^{2 n - 2} (n - 1)!}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum