Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 128955 by mathmax by abdo last updated on 11/Jan/21

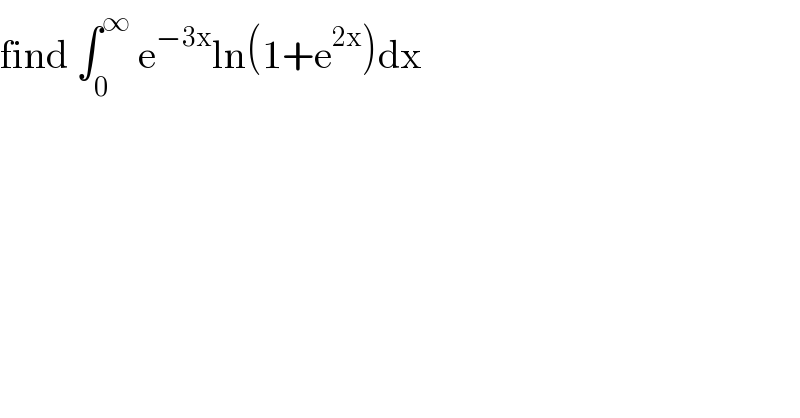
find ∫_0 ^∞ e^(−3x) ln(1+e^(2x) )dx

$$\mathrm{find}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{3x}} \mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{\mathrm{2x}} \right)\mathrm{dx} \\ $$

Answered by Dwaipayan Shikari last updated on 11/Jan/21

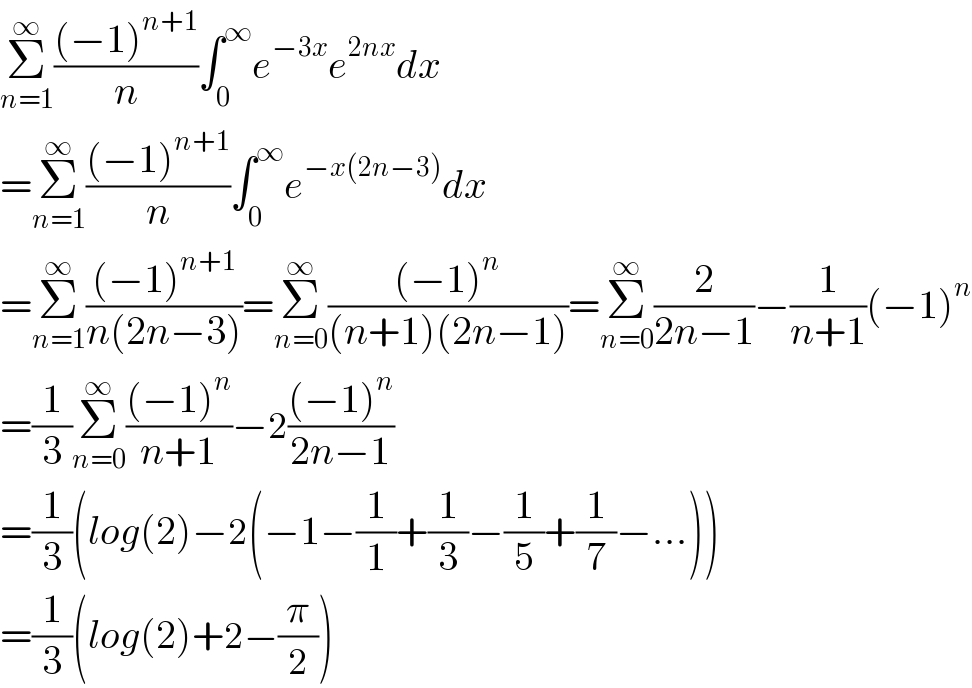
Σ_(n=1) ^∞ (((−1)^(n+1) )/n)∫_0 ^∞ e^(−3x) e^(2nx) dx =Σ_(n=1) ^∞ (((−1)^(n+1) )/n)∫_0 ^∞ e^(−x(2n−3)) dx =Σ_(n=1) ^∞ (((−1)^(n+1) )/(n(2n−3)))=Σ_(n=0) ^∞ (((−1)^n )/((n+1)(2n−1)))=Σ_(n=0) ^∞ (2/(2n−1))−(1/(n+1))(−1)^n =(1/3)Σ_(n=0) ^∞ (((−1)^n )/(n+1))−2(((−1)^n )/(2n−1)) =(1/3)(log(2)−2(−1−(1/1)+(1/3)−(1/5)+(1/7)−...)) =(1/3)(log(2)+2−(π/2))

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}}\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{3}{x}} {e}^{\mathrm{2}{nx}} {dx} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}}\int_{\mathrm{0}} ^{\infty} {e}^{−{x}\left(\mathrm{2}{n}−\mathrm{3}\right)} {dx} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}\left(\mathrm{2}{n}−\mathrm{3}\right)}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}−\mathrm{1}\right)}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}}{\mathrm{2}{n}−\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\left(−\mathrm{1}\right)^{{n}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}−\mathrm{2}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left({log}\left(\mathrm{2}\right)−\mathrm{2}\left(−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{7}}−...\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left({log}\left(\mathrm{2}\right)+\mathrm{2}−\frac{\pi}{\mathrm{2}}\right) \\ $$

Answered by Olaf last updated on 11/Jan/21

Ω = ∫_0 ^∞ e^(−3x) ln(1+e^(2x) )dx Let u = e^x Ω = ∫_1 ^∞ ((ln(1+u^2 ))/u^4 )du Ω = [−(1/3)e^(−3x) ln(1+e^(2x) )]_0 ^∞ +∫_0 ^∞ (1/3)e^(−3x) ((2e^(2x) )/(1+e^(2x) ))dx Ω = ((ln2)/3)+(2/3)∫_0 ^∞ (e^(−x) /(1+e^(2x) ))dx Let u = e^x Ω = ((ln2)/3)+(2/3)∫_1 ^∞ (du/(u^2 (1+u^2 ))) Ω = ((ln2)/3)+(2/3)∫_1 ^∞ ((1/u^2 )−(1/(1+u^2 )))du Ω = ((ln2)/3)−(2/3)[(1/u)+arctanu]_1 ^∞ Ω = ((ln2)/3)−(2/3)((π/4)−1) Ω = ((ln2)/3)+(2/3)−(π/6)

$$\Omega\:=\:\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{3}{x}} \mathrm{ln}\left(\mathrm{1}+{e}^{\mathrm{2}{x}} \right){dx} \\ $$$$\mathrm{Let}\:{u}\:=\:{e}^{{x}} \\ $$$$\Omega\:=\:\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{ln}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}{{u}^{\mathrm{4}} }{du} \\ $$$$\Omega\:=\:\left[−\frac{\mathrm{1}}{\mathrm{3}}{e}^{−\mathrm{3}{x}} \mathrm{ln}\left(\mathrm{1}+{e}^{\mathrm{2}{x}} \right)\right]_{\mathrm{0}} ^{\infty} +\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{3}}{e}^{−\mathrm{3}{x}} \frac{\mathrm{2}{e}^{\mathrm{2}{x}} }{\mathrm{1}+{e}^{\mathrm{2}{x}} }{dx} \\ $$$$\Omega\:=\:\frac{\mathrm{ln2}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}} }{\mathrm{1}+{e}^{\mathrm{2}{x}} }{dx} \\ $$$$\mathrm{Let}\:{u}\:=\:{e}^{{x}} \\ $$$$\Omega\:=\:\frac{\mathrm{ln2}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{1}} ^{\infty} \frac{{du}}{{u}^{\mathrm{2}} \left(\mathrm{1}+{u}^{\mathrm{2}} \right)} \\ $$$$\Omega\:=\:\frac{\mathrm{ln2}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{1}} ^{\infty} \left(\frac{\mathrm{1}}{{u}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\right){du} \\ $$$$\Omega\:=\:\frac{\mathrm{ln2}}{\mathrm{3}}−\frac{\mathrm{2}}{\mathrm{3}}\left[\frac{\mathrm{1}}{{u}}+\mathrm{arctan}{u}\right]_{\mathrm{1}} ^{\infty} \\ $$$$\Omega\:=\:\frac{\mathrm{ln2}}{\mathrm{3}}−\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{\pi}{\mathrm{4}}−\mathrm{1}\right) \\ $$$$\Omega\:=\:\frac{\mathrm{ln2}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}}−\frac{\pi}{\mathrm{6}} \\ $$

Answered by mathmax by abdo last updated on 11/Jan/21

let A =∫_0 ^∞ e^(−3x) ln(1+e^(2x) )dx we do the changement e^x =t ⇒ A =∫_1 ^(+∞) (1/t^3 )ln(1+t^2 )(dt/t) =∫_1 ^∞ t^(−4) ln(1+t^2 )dt =_(byparts) [−(1/3)t^(−3) ln(1+t^2 )]_1 ^∞ +(1/3)∫_1 ^∞ t^(−3) ×((2t)/(1+t^2 ))dt =((ln2)/3) +(2/3)∫_1 ^∞ (dt/(t^2 (t^2 +1))) but ∫_1 ^∞ (dt/(t^2 (t^2 +1)))=∫_1 ^∞ ((1/t^2 )−(1/(1+t^2 )))dt =∫_1 ^∞ (dt/t^2 )−∫_1 ^∞ (dt/(1+t^2 ))=[−(1/t)]_1 ^∞ −[arctant]_1 ^∞ =1−{(π/2)−(π/4)} =1−(π/4) ⇒A=((ln2)/3)+(2/3)(1−(π/4)) =((ln2)/3)+(2/3)−(π/6)

$$\mathrm{let}\:\mathrm{A}\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{3x}} \mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{\mathrm{2x}} \right)\mathrm{dx}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{e}^{\mathrm{x}} \:=\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{A}\:=\int_{\mathrm{1}} ^{+\infty} \:\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{3}} }\mathrm{ln}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\frac{\mathrm{dt}}{\mathrm{t}}\:=\int_{\mathrm{1}} ^{\infty} \:\mathrm{t}^{−\mathrm{4}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\mathrm{dt} \\ $$$$=_{\mathrm{byparts}} \:\:\:\:\:\left[−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{t}^{−\mathrm{3}} \mathrm{ln}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\right]_{\mathrm{1}} ^{\infty} +\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{1}} ^{\infty} \:\mathrm{t}^{−\mathrm{3}} ×\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{ln2}}{\mathrm{3}}\:+\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)}\:\:\mathrm{but}\:\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)}=\int_{\mathrm{1}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)\mathrm{dt} \\ $$$$=\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} }−\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }=\left[−\frac{\mathrm{1}}{\mathrm{t}}\right]_{\mathrm{1}} ^{\infty} −\left[\mathrm{arctant}\right]_{\mathrm{1}} ^{\infty} \\ $$$$=\mathrm{1}−\left\{\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\right\}\:=\mathrm{1}−\frac{\pi}{\mathrm{4}}\:\Rightarrow\mathrm{A}=\frac{\mathrm{ln2}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}−\frac{\pi}{\mathrm{4}}\right) \\ $$$$=\frac{\mathrm{ln2}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}}−\frac{\pi}{\mathrm{6}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com