Question Number 128977 by mnjuly1970 last updated on 11/Jan/21
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:...\:{nice}\:\:{calculus}... \\ $$$$\:\:\:\:\mathscr{E}{valuate}\:::: \\ $$$$\:\:\:\:\:\:\mathrm{I}:=\int_{\mathrm{0}} ^{\:\mathrm{1}} {ln}\left(\frac{\mathrm{1}}{{x}}\:−\:{x}\right)\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:=? \\ $$$$\:\:\:\:\:\:\:\ast....................................\ast \\ $$
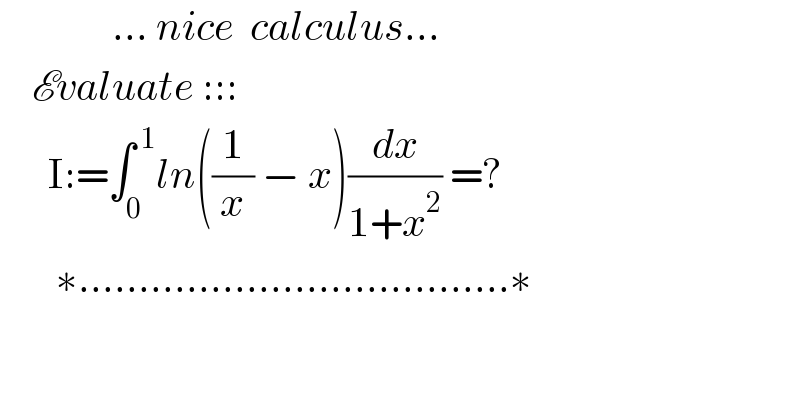
Answered by abderrahimelmerrouni last updated on 11/Jan/21
$$\mathrm{3} \\ $$
Answered by mathmax by abdo last updated on 12/Jan/21
![I=∫_0 ^1 ((ln(1−x^2 )−lnx)/(1+x^2 ))dx =∫_0 ^1 ((ln(1−x^2 ))/(1+x^2 ))dx−∫_0 ^1 ((lnx)/(1+x^2 ))dx ∫_0 ^1 ((lnx)/(1+x^2 ))dx =∫_0 ^1 lnxΣ_(n=0) ^∞ (−1)^n x^(2n) dx =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^(2n) lnxdx ∫_0 ^1 x^(2n) lnxdx =[(x^(2n+1) /(2n+1))lnx]_0 ^1 −∫_0 ^1 (x^(2n) /(2n+1))dx =−(1/((2n+1)^2 )) ⇒∫_0 ^1 ((lnx)/(1+x^2 ))dx =−Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^2 ))=−k(katalan constant) ∫_0 ^1 ((ln(1−x^2 ))/(1+x^2 ))dx =∫_0 ^1 ((ln(1−x))/(1+x^2 ))dx +∫_0 ^1 ((ln(1+x))/(1+x^2 ))dx=H+K ∫_0 ^1 ((ln(1−x))/(1+x^2 ))dx =∫_0 ^1 ln(1−x)Σ_(n=0) ^∞ (−1)^n x^(2n) dx =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^(2n) ln(1−x)dx v_n =∫_0 ^1 x^(2n) ln(1−x)dx =[((x^(2n+1) −1)/(2n+1))ln(1−x)]_0 ^1 −(1/(2n+1))∫_0 ^1 (x^(2n+1) −1)×((−1)/(1−x))dx =−(1/(2n+1))∫_0 ^1 ((x^(2n+1) −1)/(x−1))dx =−(1/(2n+1))∫_0 ^1 (1+x+x^2 +...+x^(2n) )dx =−(1/(2n+1))∫_0 ^1 Σ_(k=0) ^(2n) x^k dx =−(1/(2n+1))Σ_(k=0) ^(2n) [(x^(k+1) /(k+1))]_0 ^1 =−(1/(2n+1))Σ_(k=0) ^(2n) (1/(k+1))=−(1/(2n+1))H_(2n+1) ⇒∫_0 ^1 ((ln(1−x))/(1+x^2 ))dx =−Σ_(n=0) ^∞ (((−1)^n )/(2n+1))H_(2n+1) K=∫_0 ^1 ((ln(1+x))/(1+x^2 ))dx =_(x=tanθ) ∫_0 ^(π/4) ((ln(1+tanθ))/(1+tan^2 θ))(1+tan^2 θ)dθ =∫_0 ^(π/4) ln(1+tanθ)dθ the value of this integral is known see the platform...](Q128991.png)
$$\mathrm{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)−\mathrm{lnx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{lnx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{lnx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{lnx}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{2n}} \:\mathrm{dx}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{2n}} \mathrm{lnxdx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{2n}} \mathrm{lnxdx}\:=\left[\frac{\mathrm{x}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{2n}+\mathrm{1}}\mathrm{lnx}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{2n}} }{\mathrm{2n}+\mathrm{1}}\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{lnx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }=−\mathrm{k}\left(\mathrm{katalan}\:\mathrm{constant}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}=\mathrm{H}+\mathrm{K} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{2n}} \mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{2n}} \mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\mathrm{dx} \\ $$$$\mathrm{v}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{2n}} \mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\mathrm{dx}\:=\left[\frac{\mathrm{x}^{\mathrm{2n}+\mathrm{1}} −\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{x}^{\mathrm{2n}+\mathrm{1}} −\mathrm{1}\right)×\frac{−\mathrm{1}}{\mathrm{1}−\mathrm{x}}\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{2n}+\mathrm{1}} −\mathrm{1}}{\mathrm{x}−\mathrm{1}}\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} \:+...+\mathrm{x}^{\mathrm{2n}} \right)\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}} \:\mathrm{x}^{\mathrm{k}} \:\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}} \:\left[\frac{\mathrm{x}^{\mathrm{k}+\mathrm{1}} }{\mathrm{k}+\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}} \:\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}=−\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\mathrm{H}_{\mathrm{2n}+\mathrm{1}} \:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}+\mathrm{1}}\mathrm{H}_{\mathrm{2n}+\mathrm{1}} \\ $$$$\mathrm{K}=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=_{\mathrm{x}=\mathrm{tan}\theta} \:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{tan}\theta\right)}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)\mathrm{d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{tan}\theta\right)\mathrm{d}\theta\:\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{this}\:\mathrm{integral}\:\mathrm{is}\:\mathrm{known}\:\mathrm{see}\:\mathrm{the}\:\mathrm{platform}... \\ $$
Answered by Lordose last updated on 12/Jan/21
$$ \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{x}}\:−\:\mathrm{x}\right)\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:−\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$\Omega\:=\:\Phi\:−\:\Psi \\ $$$$\Phi\:=\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{x}^{\mathrm{2n}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{x}^{\mathrm{2n}} −\mathrm{x}^{\mathrm{2n}+\mathrm{2}} }{\mathrm{1}−\mathrm{x}^{\mathrm{4}} } \\ $$$$\mathrm{x}\:=\:\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{4}}} \:\Rightarrow\:\mathrm{dx}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{u}^{−\frac{\mathrm{3}}{\mathrm{4}}} \mathrm{du} \\ $$$$\Phi\:\overset{\mathrm{u}=\mathrm{x}^{\mathrm{4}} } {=}\frac{\mathrm{1}}{\mathrm{4}}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{u}^{\frac{\mathrm{2n}−\mathrm{3}}{\mathrm{4}}} −\:\mathrm{u}^{\frac{\mathrm{2n}−\mathrm{1}}{\mathrm{4}}} }{\mathrm{1}−\mathrm{u}}\mathrm{du}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}}\left(\mathrm{H}_{\left(\frac{\mathrm{2n}−\mathrm{1}}{\mathrm{4}}\right)} −\mathrm{H}_{\left(\frac{\mathrm{2n}−\mathrm{3}}{\mathrm{4}}\right)} \right) \\ $$$$\Phi\:=\:\frac{\mathrm{1}}{\mathrm{4}}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}}\left(\boldsymbol{\psi}^{\mathrm{0}} \left(\frac{\mathrm{n}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}\right)\:−\:\boldsymbol{\psi}^{\mathrm{0}} \left(\frac{\mathrm{n}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\right)\right) \\ $$$$\Psi\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=\:−\mathrm{G} \\ $$$$\Omega\:=\:\frac{\mathrm{1}}{\mathrm{4}}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\boldsymbol{\psi}^{\mathrm{0}} \left(\frac{\mathrm{n}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}\right)}{\mathrm{n}}\:−\:\frac{\mathrm{1}}{\mathrm{4}}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\boldsymbol{\psi}^{\mathrm{0}} \left(\frac{\mathrm{n}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\right)}{\mathrm{n}}\:+\:\mathrm{G}\:=\:\frac{\pi\mathrm{log}\left(\mathrm{2}\right)}{\mathrm{4}} \\ $$