Question Number 129001 by pipin last updated on 12/Jan/21
$$\: \\ $$$$\:\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} \:}\:=\:... \\ $$
Answered by Ar Brandon last updated on 12/Jan/21
![Φ=∫_1 ^∞ (dx/(1+x^4 ))=(1/2)∫_1 ^∞ {((x^2 +1)/(x^4 +1))−((x^2 −1)/(x^4 +1))}dx =(1/2)∫_1 ^∞ {((1+(1/x^2 ))/(x^2 +(1/x^2 )))−((1−(1/x^2 ))/(x^2 +(1/x^2 )))}dx=(1/2)∫_1 ^∞ {((1+(1/x^2 ))/((x−(1/x))^2 +2))−((1−(1/x^2 ))/((x+(1/x))^2 −2))}dx =(1/2){∫_0 ^∞ (du/(u^2 +2))−∫_2 ^∞ (dv/(v^2 −2))}=(1/2){[((tan^(−1) (u/(√2)))/( (√2)))]_0 ^∞ −(1/(2(√2)))[ln∣(((√2)+v)/( (√2)−v))∣]_2 ^∞ } =(1/2){(π/(2(√2)))+(1/(2(√2)))ln∣(((√2)+2)/( (√2)−2))∣}](Q129006.png)
$$\Phi=\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\infty} \left\{\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{x}^{\mathrm{4}} +\mathrm{1}}−\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{x}^{\mathrm{4}} +\mathrm{1}}\right\}\mathrm{dx} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\infty} \left\{\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}{\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}−\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}{\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}\right\}\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\infty} \left\{\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} +\mathrm{2}}−\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} −\mathrm{2}}\right\}\mathrm{dx} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} +\mathrm{2}}−\int_{\mathrm{2}} ^{\infty} \frac{\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} −\mathrm{2}}\right\}=\frac{\mathrm{1}}{\mathrm{2}}\left\{\left[\frac{\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{u}/\sqrt{\mathrm{2}}\right)}{\:\sqrt{\mathrm{2}}}\right]_{\mathrm{0}} ^{\infty} −\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left[\mathrm{ln}\mid\frac{\sqrt{\mathrm{2}}+\mathrm{v}}{\:\sqrt{\mathrm{2}}−\mathrm{v}}\mid\right]_{\mathrm{2}} ^{\infty} \right\} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\mid\frac{\sqrt{\mathrm{2}}+\mathrm{2}}{\:\sqrt{\mathrm{2}}−\mathrm{2}}\mid\right\} \\ $$
Commented by pipin last updated on 12/Jan/21
$$\:\mathrm{omg},\:\mathrm{thankyou}\:\mathrm{bro}\: \\ $$
Commented by Ar Brandon last updated on 12/Jan/21
You're welcome bro.
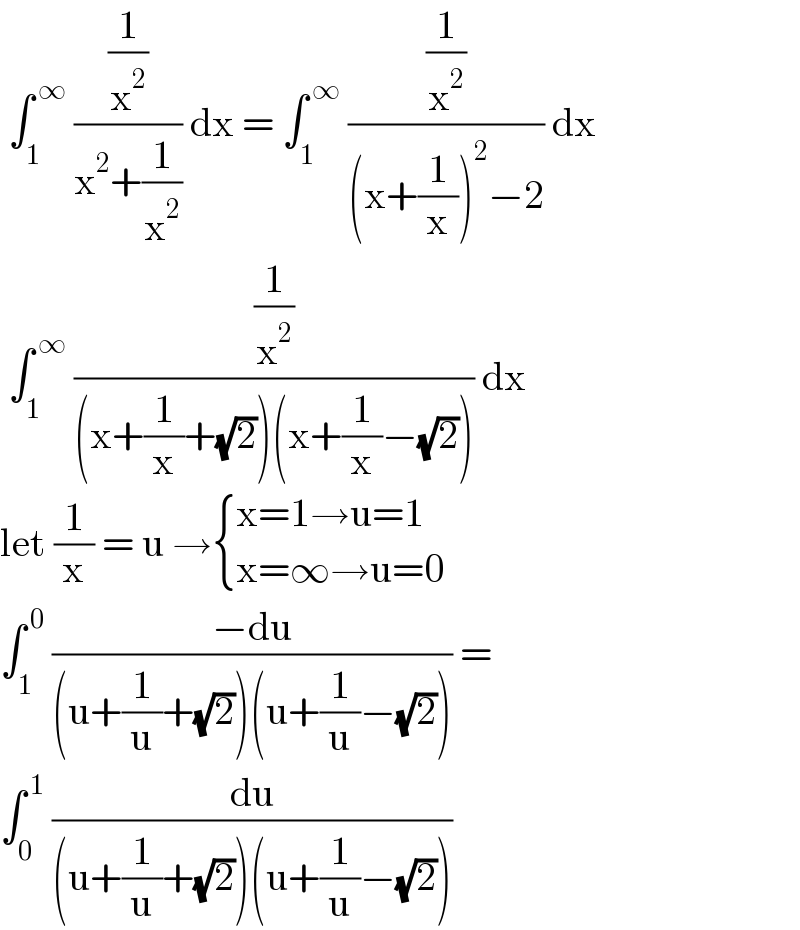
Answered by bramlexs22 last updated on 12/Jan/21
$$\:\int_{\mathrm{1}} ^{\:\infty} \:\frac{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}{\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}\:\mathrm{dx}\:=\:\int_{\mathrm{1}} ^{\:\infty} \:\frac{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} −\mathrm{2}}\:\mathrm{dx} \\ $$$$\:\int_{\mathrm{1}} ^{\:\infty} \:\frac{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}+\sqrt{\mathrm{2}}\right)\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}−\sqrt{\mathrm{2}}\right)}\:\mathrm{dx} \\ $$$$\mathrm{let}\:\frac{\mathrm{1}}{\mathrm{x}}\:=\:\mathrm{u}\:\rightarrow\begin{cases}{\mathrm{x}=\mathrm{1}\rightarrow\mathrm{u}=\mathrm{1}}\\{\mathrm{x}=\infty\rightarrow\mathrm{u}=\mathrm{0}}\end{cases} \\ $$$$\int_{\mathrm{1}} ^{\:\mathrm{0}} \:\frac{−\mathrm{du}}{\left(\mathrm{u}+\frac{\mathrm{1}}{\mathrm{u}}+\sqrt{\mathrm{2}}\right)\left(\mathrm{u}+\frac{\mathrm{1}}{\mathrm{u}}−\sqrt{\mathrm{2}}\right)}\:= \\ $$$$\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{du}}{\left(\mathrm{u}+\frac{\mathrm{1}}{\mathrm{u}}+\sqrt{\mathrm{2}}\right)\left(\mathrm{u}+\frac{\mathrm{1}}{\mathrm{u}}−\sqrt{\mathrm{2}}\right)} \\ $$