Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 129233 by MrJoe last updated on 14/Jan/21

prove that sin 3x=2cos(((3x)/2))sin(((3x)/2))

$${prove}\:{that} \\ $$$${sin}\:\mathrm{3}{x}=\mathrm{2}{cos}\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right){sin}\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right) \\ $$

Commented by MrJoe last updated on 15/Jan/21

then if sin(3x)=sin[2(((3x)/2))] form sin2x=2sinx cosx sin3x = 2sin(((3x)/2))cos(((3x)/2))

$${then}\: \\ $$$${if}\:{sin}\left(\mathrm{3}{x}\right)={sin}\left[\mathrm{2}\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)\right] \\ $$$${form}\:{sin}\mathrm{2}{x}=\mathrm{2}{sinx}\:{cosx}\: \\ $$$${sin}\mathrm{3}{x}\:=\:\mathrm{2}{sin}\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right){cos}\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right) \\ $$

Commented by MJS_new last updated on 15/Jan/21

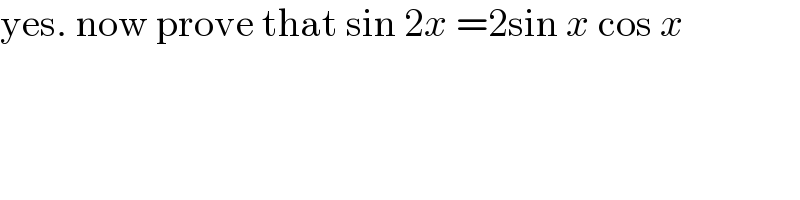
yes. now prove that sin 2x =2sin x cos x

$$\mathrm{yes}.\:\mathrm{now}\:\mathrm{prove}\:\mathrm{that}\:\mathrm{sin}\:\mathrm{2}{x}\:=\mathrm{2sin}\:{x}\:\mathrm{cos}\:{x} \\ $$

Answered by MJS_new last updated on 14/Jan/21

sin α =((e^(iα) −e^(−iα) )/(2i))∧cos α =((e^(iα) +e^(−iα) )/2) sin 3x =((e^(3ix) −e^(−3ix) )/(2i))=((e^(6ix) −1)/(2ie^(3ix) ))= =(((e^(3ix) −1)(e^(3ix) +1))/(2ie^(3ix) ))= =((e^(i((3x)/2)) (e^(i((3x)/2)) −e^(−i((3x)/2)) )e^(i((3x)/2)) (e^(i((3x)/2)) +e^(−i((3x)/2)) ))/(2ie^(3ix) ))= =(((e^(i((3x)/2)) −e^(−i((3x)/2)) )(e^(i((3x)/2)) +e^(−i((3x)/2)) ))/(2i))= =2(((e^(i((3x)/2)) −e^(−i((3x)/2)) )(e^(i((3x)/2)) +e^(−i((3x)/2)) ))/(4i))= =2(((e^(i((3x)/2)) −e^(−i((3x)/2)) ))/(2i))×(((e^(i((3x)/2)) +e^(−i((3x)/2)) ))/2)= =2sin ((3x)/2) cos ((3x)/2)

$$\mathrm{sin}\:\alpha\:=\frac{\mathrm{e}^{\mathrm{i}\alpha} −\mathrm{e}^{−\mathrm{i}\alpha} }{\mathrm{2i}}\wedge\mathrm{cos}\:\alpha\:=\frac{\mathrm{e}^{\mathrm{i}\alpha} +\mathrm{e}^{−\mathrm{i}\alpha} }{\mathrm{2}} \\ $$$$\mathrm{sin}\:\mathrm{3}{x}\:=\frac{\mathrm{e}^{\mathrm{3i}{x}} −\mathrm{e}^{−\mathrm{3i}{x}} }{\mathrm{2i}}=\frac{\mathrm{e}^{\mathrm{6i}{x}} −\mathrm{1}}{\mathrm{2ie}^{\mathrm{3i}{x}} }= \\ $$$$=\frac{\left(\mathrm{e}^{\mathrm{3i}{x}} −\mathrm{1}\right)\left(\mathrm{e}^{\mathrm{3i}{x}} +\mathrm{1}\right)}{\mathrm{2ie}^{\mathrm{3i}{x}} }= \\ $$$$=\frac{\mathrm{e}^{\mathrm{i}\frac{\mathrm{3}{x}}{\mathrm{2}}} \left(\mathrm{e}^{\mathrm{i}\frac{\mathrm{3}{x}}{\mathrm{2}}} −\mathrm{e}^{−\mathrm{i}\frac{\mathrm{3}{x}}{\mathrm{2}}} \right)\mathrm{e}^{\mathrm{i}\frac{\mathrm{3}{x}}{\mathrm{2}}} \left(\mathrm{e}^{\mathrm{i}\frac{\mathrm{3}{x}}{\mathrm{2}}} +\mathrm{e}^{−\mathrm{i}\frac{\mathrm{3}{x}}{\mathrm{2}}} \right)}{\mathrm{2ie}^{\mathrm{3i}{x}} }= \\ $$$$=\frac{\left(\mathrm{e}^{\mathrm{i}\frac{\mathrm{3}{x}}{\mathrm{2}}} −\mathrm{e}^{−\mathrm{i}\frac{\mathrm{3}{x}}{\mathrm{2}}} \right)\left(\mathrm{e}^{\mathrm{i}\frac{\mathrm{3}{x}}{\mathrm{2}}} +\mathrm{e}^{−\mathrm{i}\frac{\mathrm{3}{x}}{\mathrm{2}}} \right)}{\mathrm{2i}}= \\ $$$$=\mathrm{2}\frac{\left(\mathrm{e}^{\mathrm{i}\frac{\mathrm{3}{x}}{\mathrm{2}}} −\mathrm{e}^{−\mathrm{i}\frac{\mathrm{3}{x}}{\mathrm{2}}} \right)\left(\mathrm{e}^{\mathrm{i}\frac{\mathrm{3}{x}}{\mathrm{2}}} +\mathrm{e}^{−\mathrm{i}\frac{\mathrm{3}{x}}{\mathrm{2}}} \right)}{\mathrm{4i}}= \\ $$$$=\mathrm{2}\frac{\left(\mathrm{e}^{\mathrm{i}\frac{\mathrm{3}{x}}{\mathrm{2}}} −\mathrm{e}^{−\mathrm{i}\frac{\mathrm{3}{x}}{\mathrm{2}}} \right)}{\mathrm{2i}}×\frac{\left(\mathrm{e}^{\mathrm{i}\frac{\mathrm{3}{x}}{\mathrm{2}}} +\mathrm{e}^{−\mathrm{i}\frac{\mathrm{3}{x}}{\mathrm{2}}} \right)}{\mathrm{2}}= \\ $$$$=\mathrm{2sin}\:\frac{\mathrm{3}{x}}{\mathrm{2}}\:\mathrm{cos}\:\frac{\mathrm{3}{x}}{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com