Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 129287 by math178 last updated on 14/Jan/21

Commented by math178 last updated on 14/Jan/21

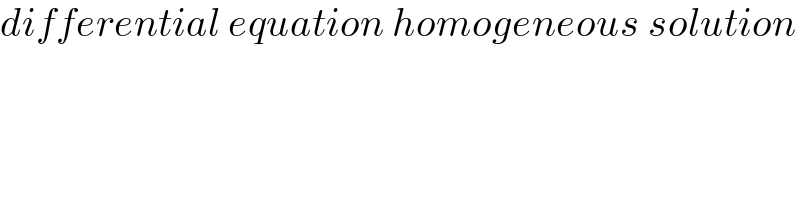
differential equation homogeneous solution

$${differential}\:{equation}\:{homogeneous}\:{solution} \\ $$

Answered by mathmax by abdo last updated on 15/Jan/21

y^((2)) −3y^((1)) +2y =(e^x /(1+e^(−x) )) h→r^2 −3r+2=0 →Δ=1 ⇒r_1 =((3+1)/2)=2 and r_2 =((3−1)/2)=1 ⇒ y_h =ae^x +be^(2x) =au_1 +bu_2 W(u_1 ,u_2 )= determinant (((e^x e^(2x) )),((e^x 2e^(2x) )))=2e^(3x) −e^(3x) =e^(3x) ≠0 W_1 = determinant (((o e^(2x) )),(((e^x /(1+e^(−x) )) 2e^(2x) )))=−(e^(3x) /(1+e^(−x) )) W_2 = determinant (((e^x 0)),((e^x (e^x /(1+e^(−x) )))))=(e^(2x) /(1+e^(−x) )) v_1 =∫ (w_1 /W)dx =−∫ (e^(3x) /((1+e^(−x) )e^(3x) ))dx =−∫ (dx/(1+e^(−x) )) =−∫ (e^x /(e^x +1))dx =−ln(e^x +1) v_2 =∫ (w_2 /W)dx =∫ (e^(2x) /((1+e^(−x) )e^(3x) ))dx =∫ (e^(−x) /(1+e^(−x) ))dx =−ln(e^(−x) +1) ⇒ y_p =u_1 v_1 +u_2 v_2 =−e^x ln(e^x +1)−e^(2x) ln(e^(−x) +1) general solution is y =y_h +y_p =ae^x +be^(2x) −e^x ln(e^x +1)−e^(2x) ln(e^(−x) +1)

$$\mathrm{y}^{\left(\mathrm{2}\right)} −\mathrm{3y}^{\left(\mathrm{1}\right)} \:+\mathrm{2y}\:=\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{x}} } \\ $$$$\mathrm{h}\rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{3r}+\mathrm{2}=\mathrm{0}\:\rightarrow\Delta=\mathrm{1}\:\Rightarrow\mathrm{r}_{\mathrm{1}} =\frac{\mathrm{3}+\mathrm{1}}{\mathrm{2}}=\mathrm{2}\:\mathrm{and}\:\mathrm{r}_{\mathrm{2}} =\frac{\mathrm{3}−\mathrm{1}}{\mathrm{2}}=\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{y}_{\mathrm{h}} =\mathrm{ae}^{\mathrm{x}} \:+\mathrm{be}^{\mathrm{2x}} \:=\mathrm{au}_{\mathrm{1}} \:+\mathrm{bu}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} ,\mathrm{u}_{\mathrm{2}} \right)=\begin{vmatrix}{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{2x}} }\\{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:\mathrm{2e}^{\mathrm{2x}} }\end{vmatrix}=\mathrm{2e}^{\mathrm{3x}} −\mathrm{e}^{\mathrm{3x}} \:=\mathrm{e}^{\mathrm{3x}} \:\neq\mathrm{0} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{o}\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{2x}} }\\{\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{x}} }\:\:\:\:\mathrm{2e}^{\mathrm{2x}} }\end{vmatrix}=−\frac{\mathrm{e}^{\mathrm{3x}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{x}} } \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{x}} }}\end{vmatrix}=\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{x}} } \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{W}}\mathrm{dx}\:=−\int\:\:\:\frac{\mathrm{e}^{\mathrm{3x}} }{\left(\mathrm{1}+\mathrm{e}^{−\mathrm{x}} \right)\mathrm{e}^{\mathrm{3x}} }\mathrm{dx}\:=−\int\:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{e}^{−\mathrm{x}} } \\ $$$$=−\int\:\:\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{e}^{\mathrm{x}} \:+\mathrm{1}}\mathrm{dx}\:=−\mathrm{ln}\left(\mathrm{e}^{\mathrm{x}} \:+\mathrm{1}\right) \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{w}_{\mathrm{2}} }{\mathrm{W}}\mathrm{dx}\:=\int\:\:\frac{\mathrm{e}^{\mathrm{2x}} }{\left(\mathrm{1}+\mathrm{e}^{−\mathrm{x}} \right)\mathrm{e}^{\mathrm{3x}} }\mathrm{dx}\:=\int\:\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{x}} }\mathrm{dx}\:=−\mathrm{ln}\left(\mathrm{e}^{−\mathrm{x}} \:+\mathrm{1}\right)\:\Rightarrow \\ $$$$\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} =−\mathrm{e}^{\mathrm{x}} \mathrm{ln}\left(\mathrm{e}^{\mathrm{x}} \:+\mathrm{1}\right)−\mathrm{e}^{\mathrm{2x}} \:\mathrm{ln}\left(\mathrm{e}^{−\mathrm{x}} \:+\mathrm{1}\right)\:\mathrm{general}\:\mathrm{solution}\:\mathrm{is} \\ $$$$\mathrm{y}\:=\mathrm{y}_{\mathrm{h}} +\mathrm{y}_{\mathrm{p}} =\mathrm{ae}^{\mathrm{x}} \:+\mathrm{be}^{\mathrm{2x}} \:−\mathrm{e}^{\mathrm{x}} \mathrm{ln}\left(\mathrm{e}^{\mathrm{x}} \:+\mathrm{1}\right)−\mathrm{e}^{\mathrm{2x}} \mathrm{ln}\left(\mathrm{e}^{−\mathrm{x}} \:+\mathrm{1}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com