Question and Answers Forum
Question Number 129344 by bramlexs22 last updated on 15/Jan/21
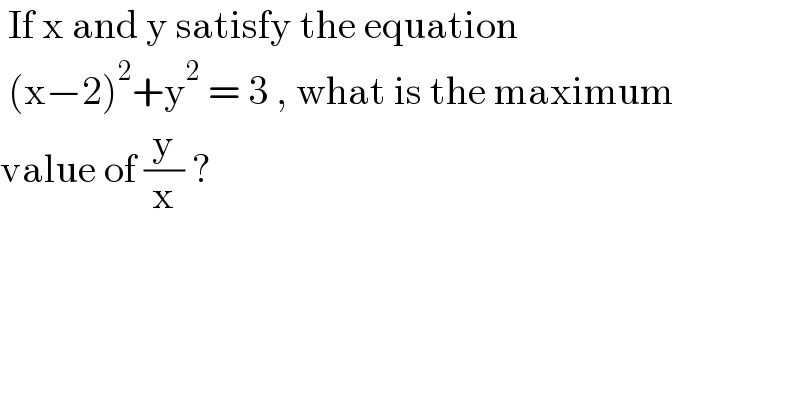
Answered by liberty last updated on 15/Jan/21
![f(x) = ((±(√(3−(x−2)^2 )))/x) = ((± (√(4x−x^2 −1)))/x) f ′(x)=± [(( x(((2−x)/( (√(4x−x^2 −1)))))−(√(4x−x^2 −1)))/x^2 ) ] =0 ⇒ ± (2x−x^2 −(4x−x^2 −1))=0 ⇒± (1−2x)=0 ⇒x = (1/2) f((1/2)) = ±((√(3−((1/2)−2)^2 ))/(1/2))=±2 (√(3/4)) ((y/x))_(max) = (√3) ; ((y/x))_(min) =−(√3)](Q129346.png)
Answered by mr W last updated on 15/Jan/21
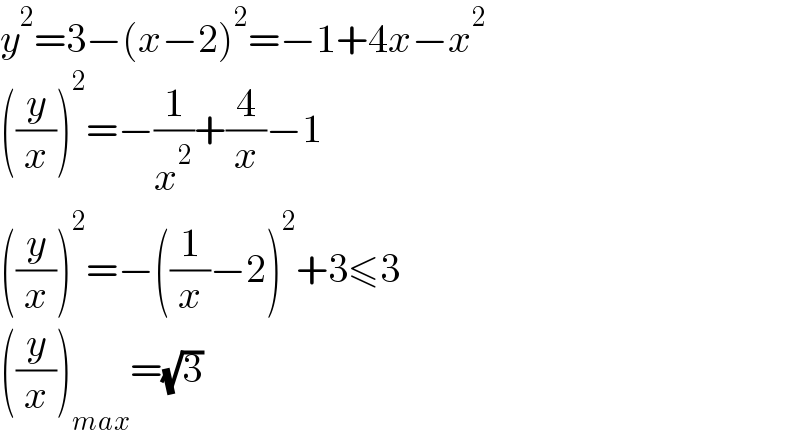
Commented by liberty last updated on 15/Jan/21
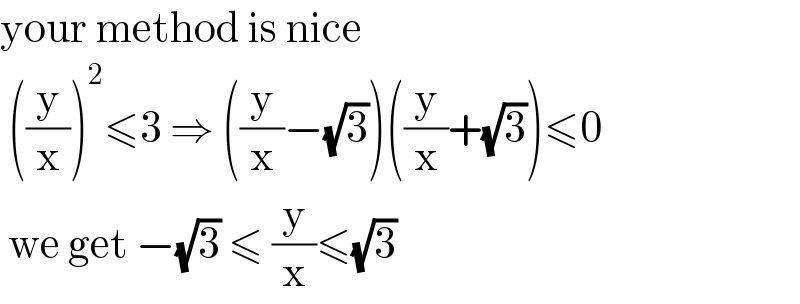
Commented by mr W last updated on 15/Jan/21

Commented by liberty last updated on 15/Jan/21
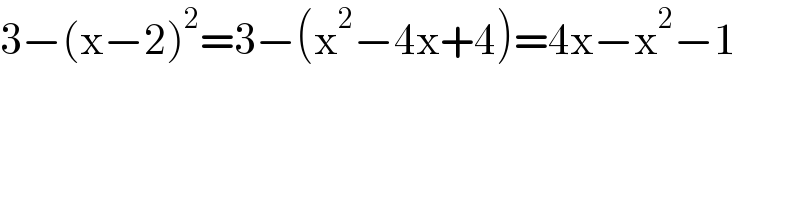
Commented by bramlexs22 last updated on 15/Jan/21

Answered by ajfour last updated on 15/Jan/21
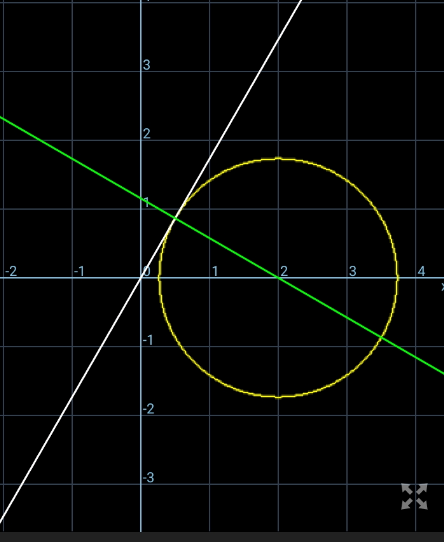
Commented by ajfour last updated on 15/Jan/21
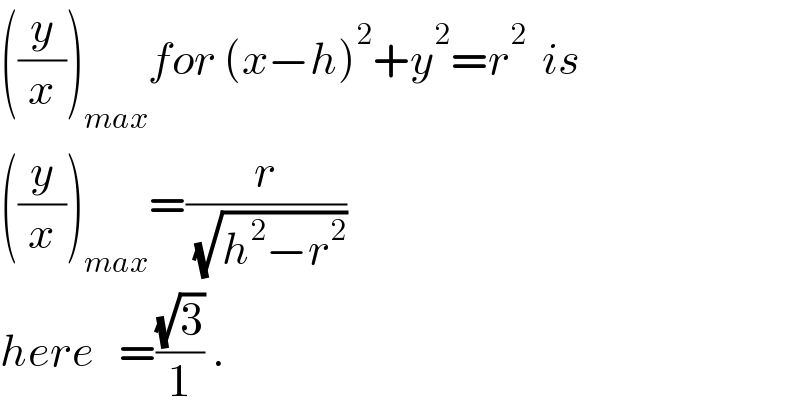
Commented by liberty last updated on 15/Jan/21
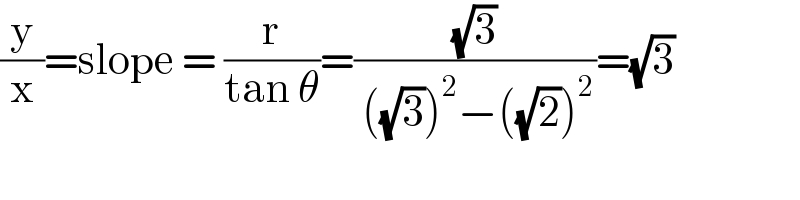
Answered by Olaf last updated on 15/Jan/21