
Question and Answers Forum
Question Number 129418 by mnjuly1970 last updated on 15/Jan/21
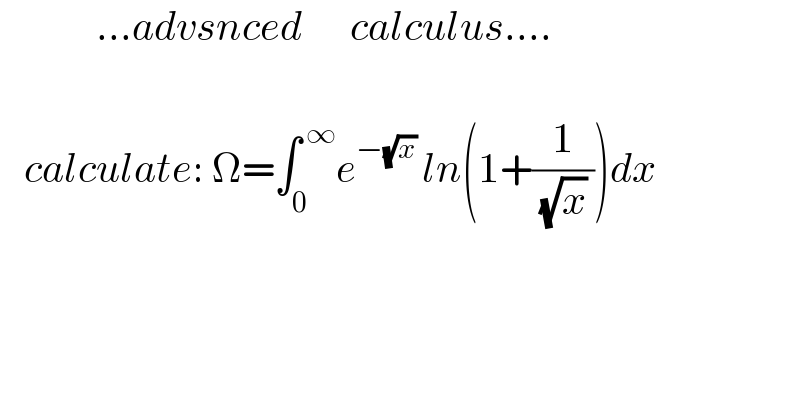
Answered by Dwaipayan Shikari last updated on 15/Jan/21
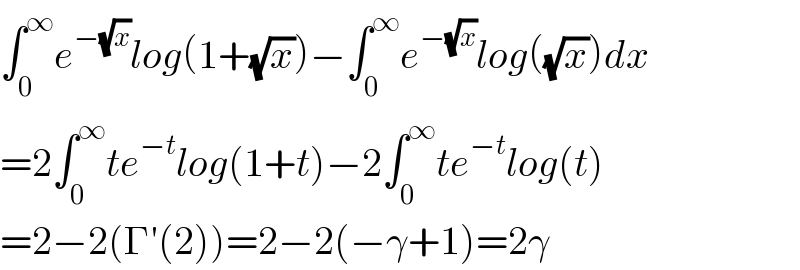
Commented by mnjuly1970 last updated on 15/Jan/21
Answered by mindispower last updated on 15/Jan/21
![(√x)=t ⇒∫_0 ^∞ e^(−t) ln(1+(1/t)).2tdt ∫ln(1+t)te^(−t) dt by part ∫te^(−t) dt=−(t+1)e^(−t) dt ∫_0 ^∞ ln(1+t)te^(−t) dt=[−(t+1)e^(−t) ln(1+t)]_0 ^∞ +∫(((t+1)e^(−t) )/(t+1))dt =∫_0 ^∞ e^(−t) dt=Γ(1)=1 ∫_0 ^∞ te^(−t) ln(t)dt=∂_x ∫_0 ^∞ t^(x−1) e^(−t) dt∣_(x=2) =Γ′(2)=Γ(2)Ψ(2) =Ψ(2)=1+Ψ(1)=1−γ ∫_0 ^∞ e^(−t) ln(1+(1/t)).2tdt=2∫_0 ^∞ e^(−t) ln(1+t)tdt−2∫_0 ^∞ e^(−t) tln(t)dt =2.1−2(1−γ)=2γ](Q129432.png)
Commented by mnjuly1970 last updated on 16/Jan/21
Answered by Lordose last updated on 16/Jan/21
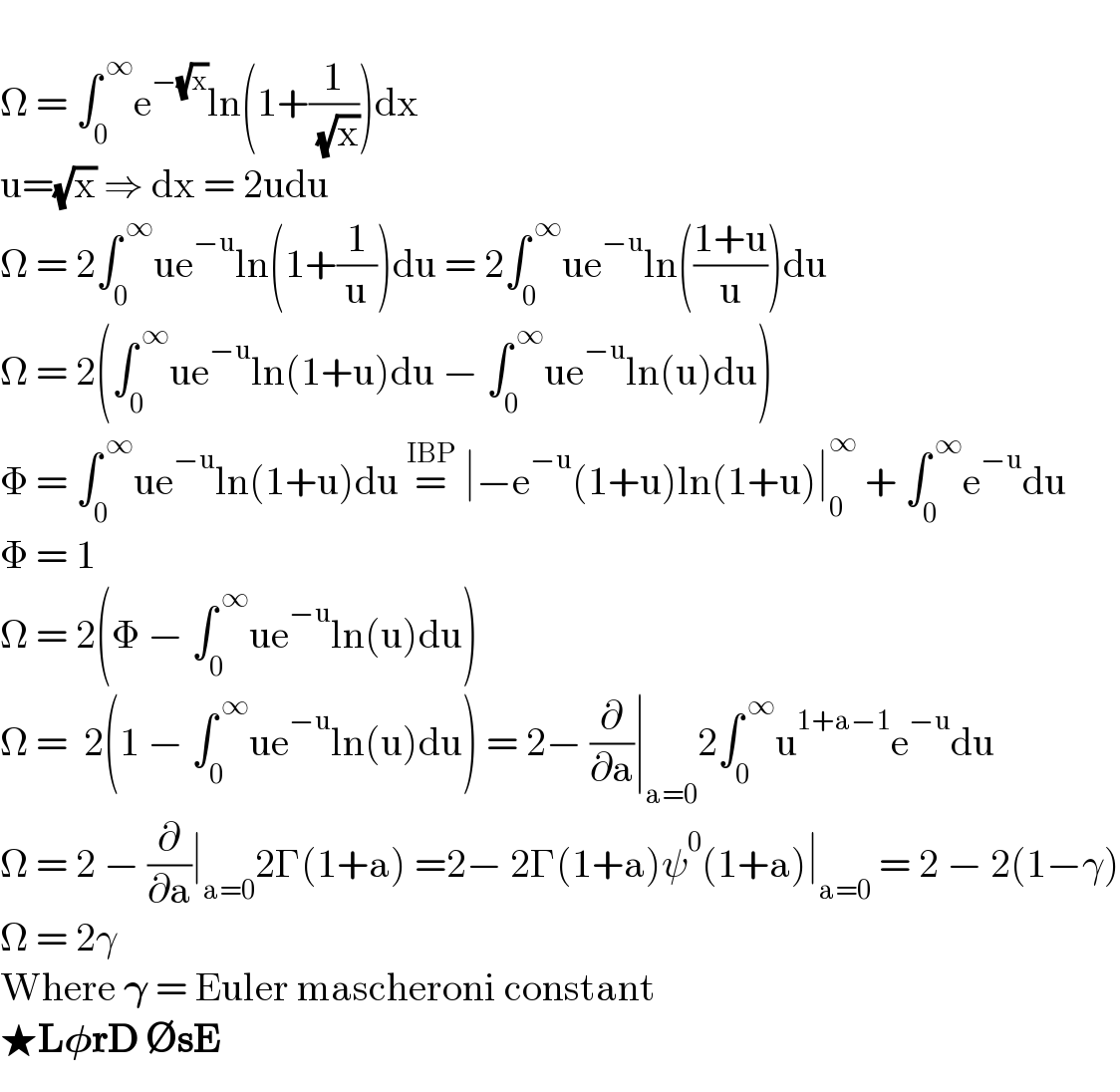
Commented by mnjuly1970 last updated on 16/Jan/21

