Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 129763 by Eric002 last updated on 18/Jan/21

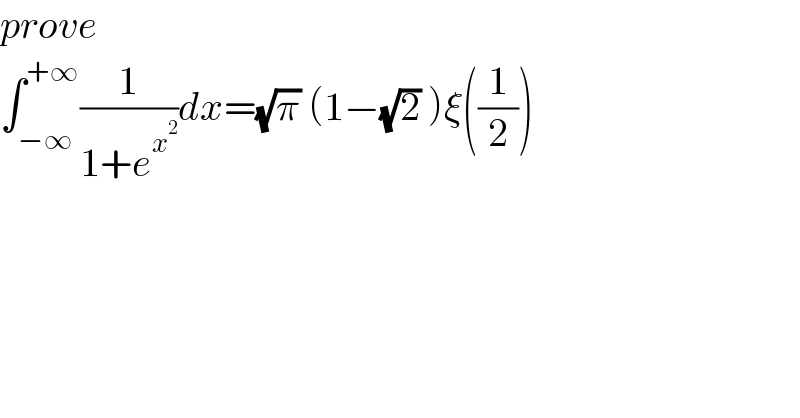
prove ∫_(−∞) ^(+∞) (1/(1+e^x^2 ))dx=(√π) (1−(√2) )ξ((1/2))

$${prove} \\ $$$$\int_{−\infty} ^{+\infty} \frac{\mathrm{1}}{\mathrm{1}+{e}^{{x}^{\mathrm{2}} } }{dx}=\sqrt{\pi}\:\left(\mathrm{1}−\sqrt{\mathrm{2}}\:\right)\xi\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$

Answered by Dwaipayan Shikari last updated on 18/Jan/21

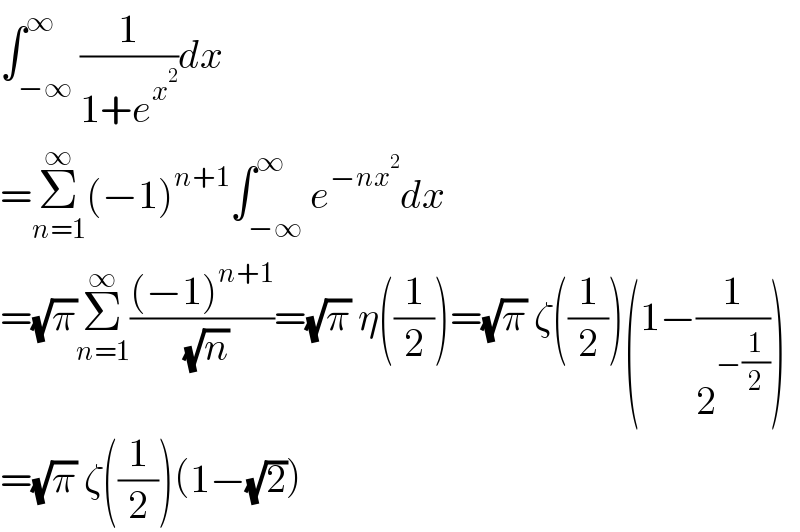
∫_(−∞) ^∞ (1/(1+e^x^2 ))dx =Σ_(n=1) ^∞ (−1)^(n+1) ∫_(−∞) ^∞ e^(−nx^2 ) dx =(√π)Σ_(n=1) ^∞ (((−1)^(n+1) )/( (√n)))=(√π) η((1/2))=(√π) ζ((1/2))(1−(1/2^(−(1/2)) )) =(√π) ζ((1/2))(1−(√2))

$$\int_{−\infty} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+{e}^{{x}^{\mathrm{2}} } }{dx} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \int_{−\infty} ^{\infty} {e}^{−{nx}^{\mathrm{2}} } {dx} \\ $$$$=\sqrt{\pi}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\:\sqrt{{n}}}=\sqrt{\pi}\:\eta\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\sqrt{\pi}\:\zeta\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{−\frac{\mathrm{1}}{\mathrm{2}}} }\right) \\ $$$$=\sqrt{\pi}\:\zeta\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}−\sqrt{\mathrm{2}}\right) \\ $$

Commented by Eric002 last updated on 18/Jan/21

well done

$${well}\:{done}\: \\ $$

Answered by mnjuly1970 last updated on 18/Jan/21

φ=2∫_0 ^( ∞) (1/(1+e^x^2 ))dx=^(x^2 =t) ∫_0 ^( ∞) (dt/( (√t) (1+e^t ))) =∫_(0 ) ^( ∞) (t^((1/2) −1) /(1+e^t )) =Γ(s).η(s) where Γ and η are Euler gamma and Drichlet etafunctions respectively. ∴ φ = Γ((1/2))η((1/2)) = Γ((1/2))(1−2^(1−(1/2)) )ζ((1/2)) = (√(π )) (1−(√(2 )) )ζ((1/2))...

$$\phi=\mathrm{2}\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{1}}{\mathrm{1}+{e}^{{x}^{\mathrm{2}} } }{dx}\overset{{x}^{\mathrm{2}} ={t}} {=}\int_{\mathrm{0}} ^{\:\infty} \frac{{dt}}{\:\sqrt{{t}}\:\left(\mathrm{1}+{e}^{{t}} \right)} \\ $$$$\:=\int_{\mathrm{0}\:\:} ^{\:\infty} \frac{{t}^{\frac{\mathrm{1}}{\mathrm{2}}\:−\mathrm{1}} }{\mathrm{1}+{e}^{{t}} }\:=\Gamma\left({s}\right).\eta\left({s}\right)\: \\ $$$$\:\:\:{where}\:\:\Gamma\:{and}\:\:\eta\:{are}\:{Euler}\:\:{gamma}\:{and} \\ $$$$\:\:\:{Drichlet}\:{etafunctions}\:{respectively}.\:\: \\ $$$$\therefore\:\phi\:=\:\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\eta\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\:\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}−\mathrm{2}^{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}} \right)\zeta\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\:\:\sqrt{\pi\:}\:\left(\mathrm{1}−\sqrt{\mathrm{2}\:}\:\right)\zeta\left(\frac{\mathrm{1}}{\mathrm{2}}\right)... \\ $$$$ \\ $$$$\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com