
Question and Answers Forum
Question Number 129764 by Eric002 last updated on 18/Jan/21
![prove that ∫_(−∞) ^(+∞) x^2 e^(−x^2 ) cos(x^2 )sin(x^2 ) dx =(((√π)sin[(((√3)tan^(−1) (2))/2)])/(4 ((125))^(1/4) ))](Q129764.png)
Answered by Dwaipayan Shikari last updated on 18/Jan/21
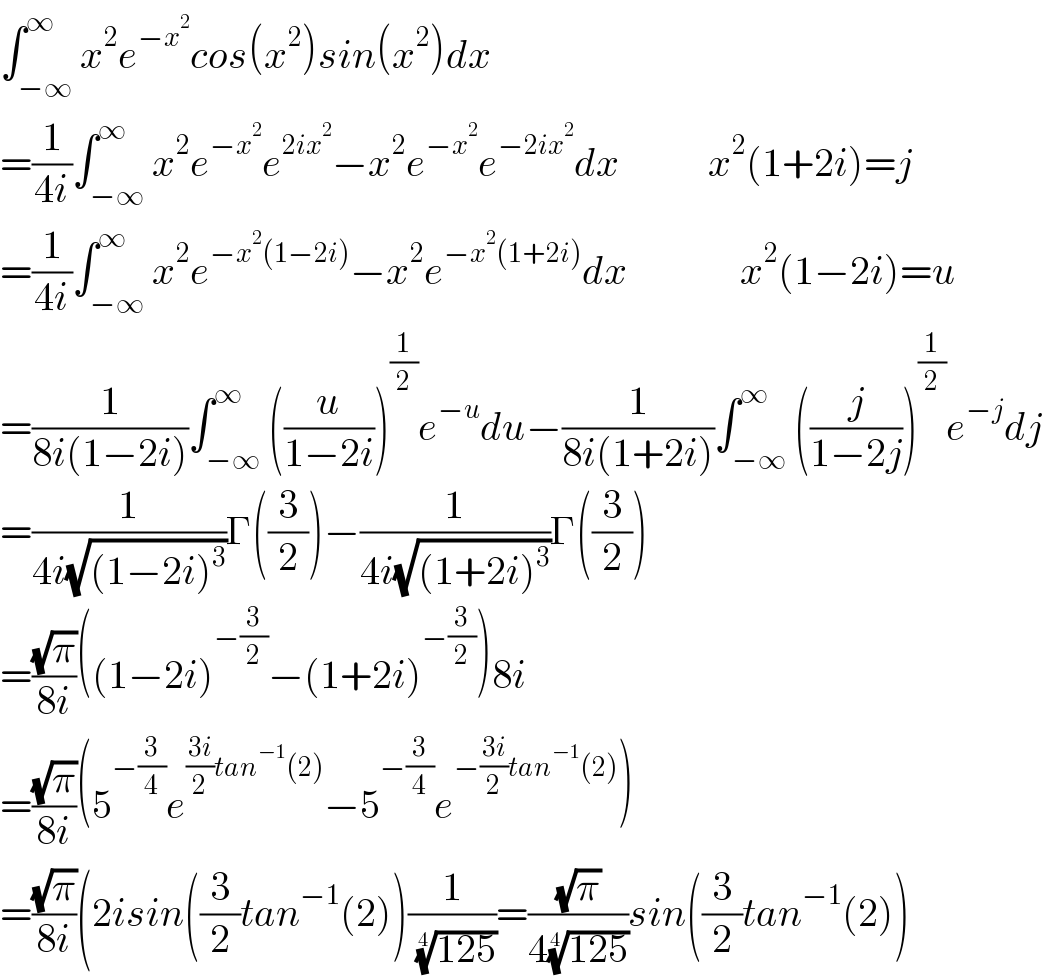
Commented by Eric002 last updated on 18/Jan/21

Answered by mathmax by abdo last updated on 18/Jan/21
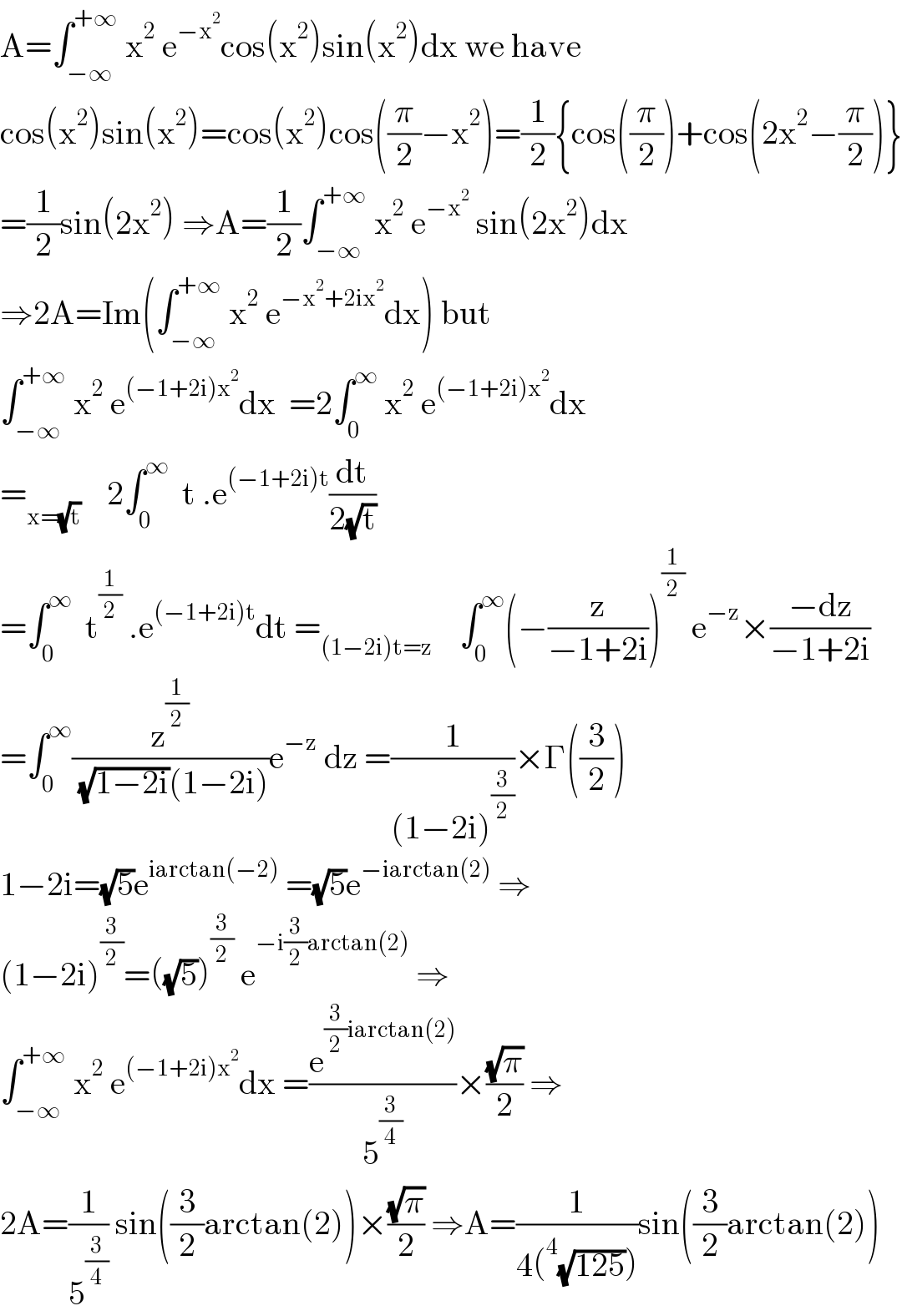
| ||
Question and Answers Forum | ||
Question Number 129764 by Eric002 last updated on 18/Jan/21 | ||
![prove that ∫_(−∞) ^(+∞) x^2 e^(−x^2 ) cos(x^2 )sin(x^2 ) dx =(((√π)sin[(((√3)tan^(−1) (2))/2)])/(4 ((125))^(1/4) ))](Q129764.png) | ||
Answered by Dwaipayan Shikari last updated on 18/Jan/21 | ||
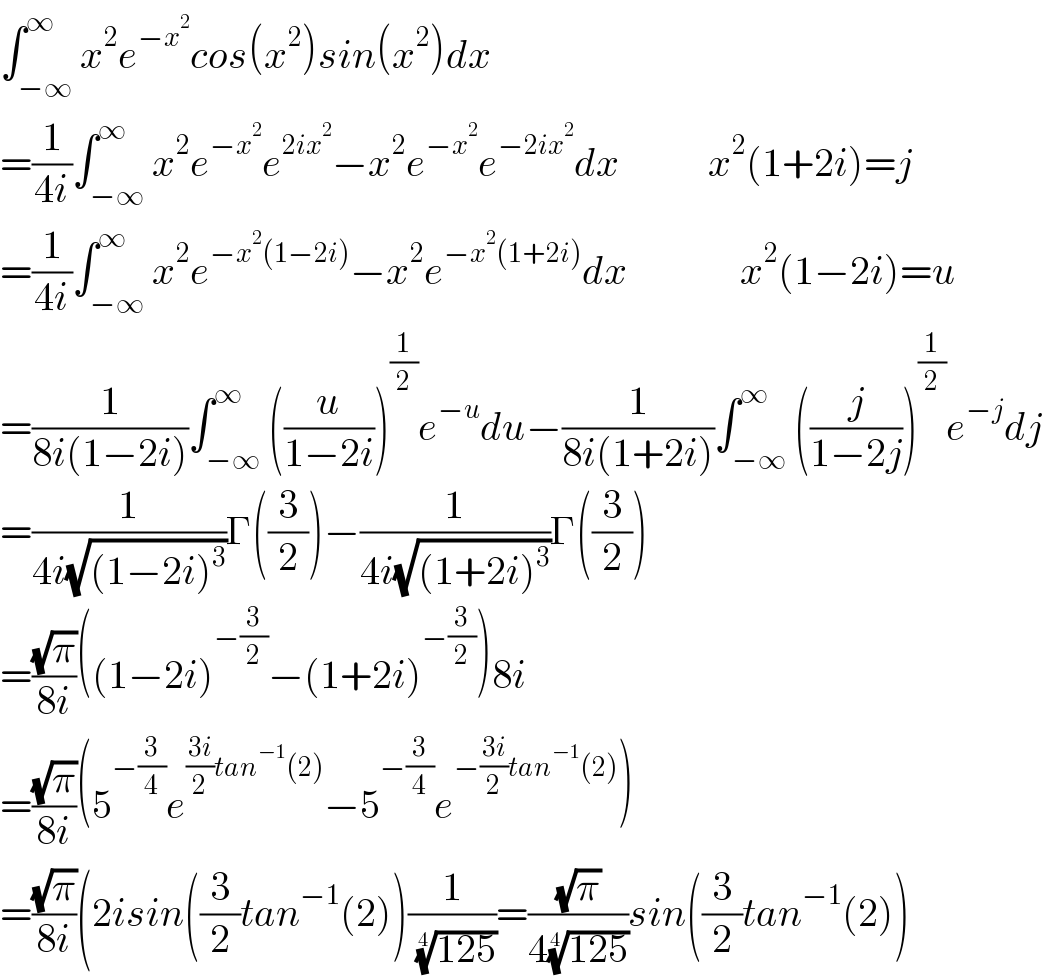 | ||
| ||
Commented by Eric002 last updated on 18/Jan/21 | ||
 | ||
Answered by mathmax by abdo last updated on 18/Jan/21 | ||
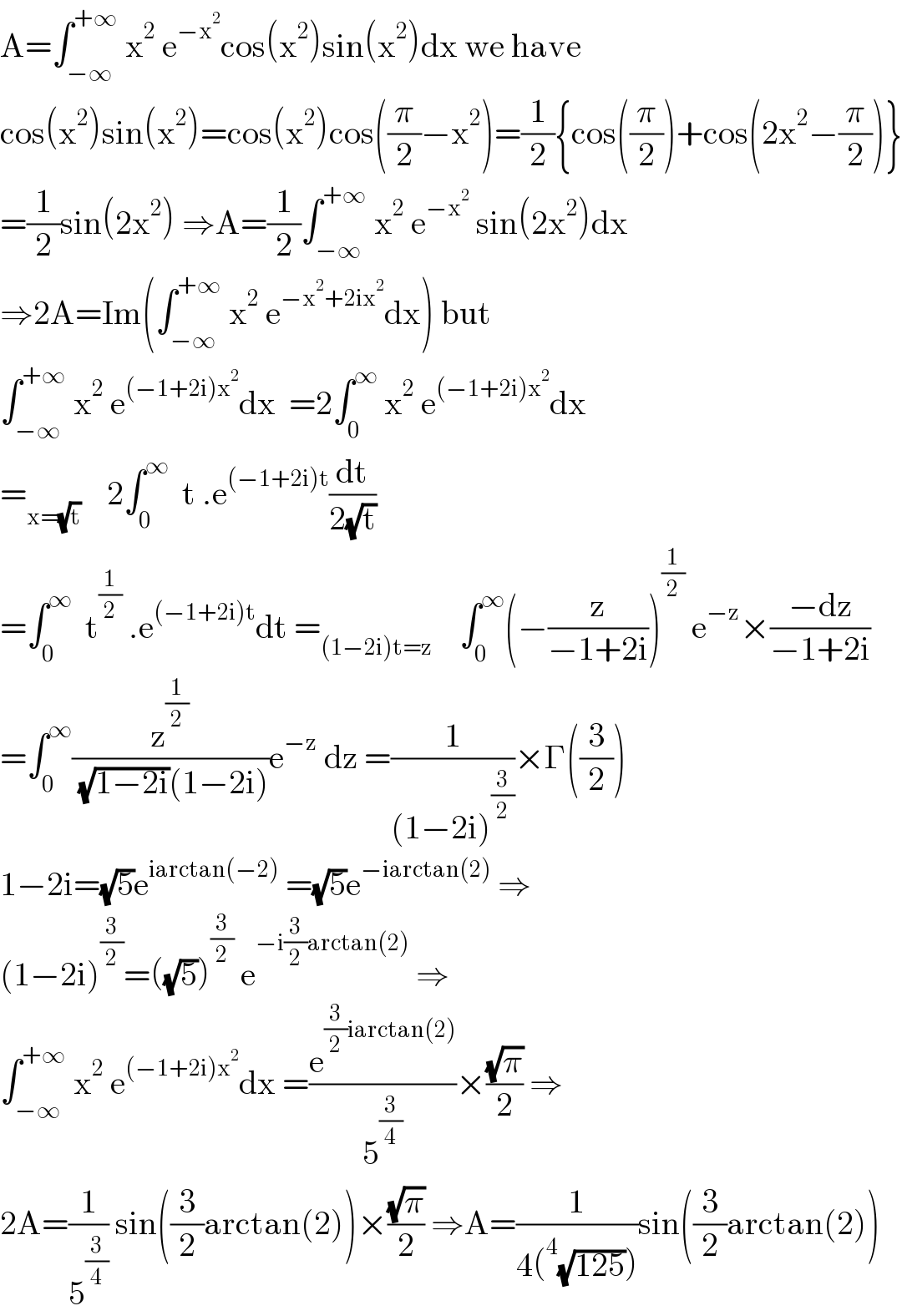 | ||
| ||