
Question and Answers Forum
Question Number 129815 by stelor last updated on 19/Jan/21
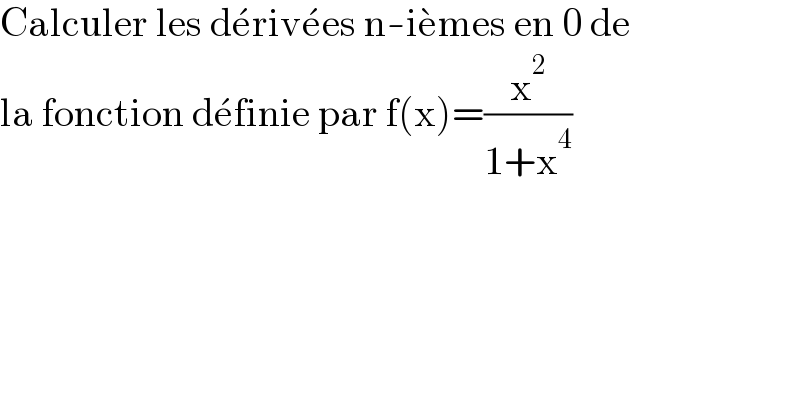
Answered by mathmax by abdo last updated on 19/Jan/21
![first let decompose f(x)=(x^2 /(x^4 +1)) z^4 +1=0 ⇒z^4 =−1=e^(i(2k+1)π) ⇒z_k =e^((i(2k+1)π)/4) and k∈[[0,3]] f(x)=(x^2 /(Π_(k=0) ^3 (x−z_k ))) =Σ_(k=0) ^3 (a_k /(x−z_k )) a_k =(z_k ^2 /(4z_k ^3 )) =(1/(4z_k )) ⇒f(x)=(1/4)Σ_(k=0) ^3 (1/(z_k (x−z_k )))=(1/4)Σ_(k=0) ^3 (e^(−i(((2k+1)π)/4)) /(x−z_k )) ⇒ f^((n)) (x)=(1/4)Σ_(k=0) ^3 e^(−((k(2k+1)π)/4)) ×(((−1)^n n!)/((x−z_k )^(n+1) )) ⇒ f^((n)) (0) =(1/4)Σ_(k=0) ^3 e^(−((i(2k+1)π)/4)) (((−1)^n n!)/((−1)^(n+1) z_k ^(n+1) )) =−(1/4)Σ_(k=0) ^3 ((n!)/z_k ^(n+2) ) =−((n!)/4)Σ_(k=0) ^3 (e^(−((i(2k+1)π)/4)) )^(n+2) =−((n!)/4)Σ_(k=0) ^3 e^(−((i(2k+1)(n+2)π)/4)) =−((n!)/4){e^(−i(n+2)(π/4)) +e^(−((3i(n+2)π)/4)) +e^(−((5i(n+2)π)/4)) + e^(−((7i(n+2)π)/4)) }](Q129829.png)
| ||
Question and Answers Forum | ||
Question Number 129815 by stelor last updated on 19/Jan/21 | ||
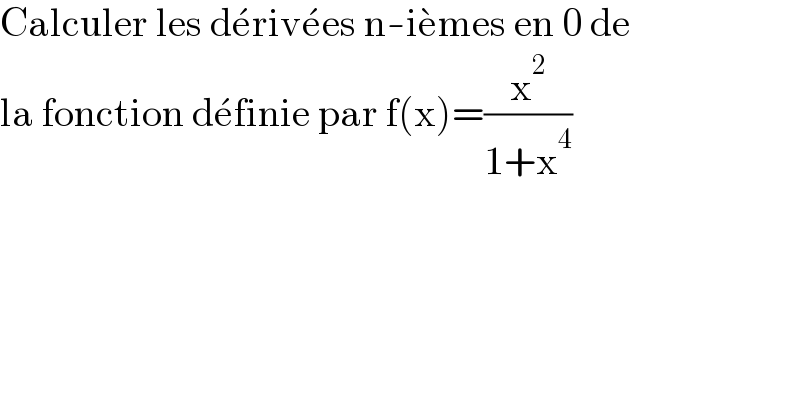 | ||
Answered by mathmax by abdo last updated on 19/Jan/21 | ||
![first let decompose f(x)=(x^2 /(x^4 +1)) z^4 +1=0 ⇒z^4 =−1=e^(i(2k+1)π) ⇒z_k =e^((i(2k+1)π)/4) and k∈[[0,3]] f(x)=(x^2 /(Π_(k=0) ^3 (x−z_k ))) =Σ_(k=0) ^3 (a_k /(x−z_k )) a_k =(z_k ^2 /(4z_k ^3 )) =(1/(4z_k )) ⇒f(x)=(1/4)Σ_(k=0) ^3 (1/(z_k (x−z_k )))=(1/4)Σ_(k=0) ^3 (e^(−i(((2k+1)π)/4)) /(x−z_k )) ⇒ f^((n)) (x)=(1/4)Σ_(k=0) ^3 e^(−((k(2k+1)π)/4)) ×(((−1)^n n!)/((x−z_k )^(n+1) )) ⇒ f^((n)) (0) =(1/4)Σ_(k=0) ^3 e^(−((i(2k+1)π)/4)) (((−1)^n n!)/((−1)^(n+1) z_k ^(n+1) )) =−(1/4)Σ_(k=0) ^3 ((n!)/z_k ^(n+2) ) =−((n!)/4)Σ_(k=0) ^3 (e^(−((i(2k+1)π)/4)) )^(n+2) =−((n!)/4)Σ_(k=0) ^3 e^(−((i(2k+1)(n+2)π)/4)) =−((n!)/4){e^(−i(n+2)(π/4)) +e^(−((3i(n+2)π)/4)) +e^(−((5i(n+2)π)/4)) + e^(−((7i(n+2)π)/4)) }](Q129829.png) | ||
| ||