
Question and Answers Forum
Question Number 129832 by ajfour last updated on 19/Jan/21

Commented by ajfour last updated on 19/Jan/21
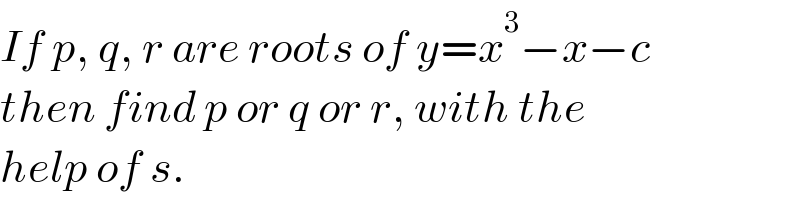
Commented by MJS_new last updated on 20/Jan/21
![my opinion: x^4 +ax^2 +bx+c=0 can be solved exactly if we can find exact factors α, β, γ with (x^2 −αx−β)(x^2 +αx−γ)=x^4 +ax^2 +bx+c ⇔ we must find at least one useable exact solution for y^3 +Py+Q=0 with P=−((a^2 +12c)/3)∧Q=−((2a^3 −72ac+27b^2 )/(27)) now what you seem to want is finding s in order to solve the following: (X^3 −X−C)(X−s)=0 ⇔ X^4 −sX^3 −X^2 −(C−s)X+Cs=0 ⇔ [X=x+(s/4)] ⇔ x^4 −((3s^2 +8)/8)x^2 −((s^3 −4s+8C)/8)x−((3s(s^3 −16s−64C))/(256))=0 ⇒ we must be able to find a solution of y^3 +Py+Q=0 with P=−((3s^2 +9Cs+1)/3) Q=−((27Cs^3 +18s^2 +27Cs+37C^2 −2)/(27)) try with C=(1/3) I don′t think you can find a fitting s following this path without solving another 3^(rd) degree polynome](Q129861.png)
Answered by ajfour last updated on 20/Jan/21
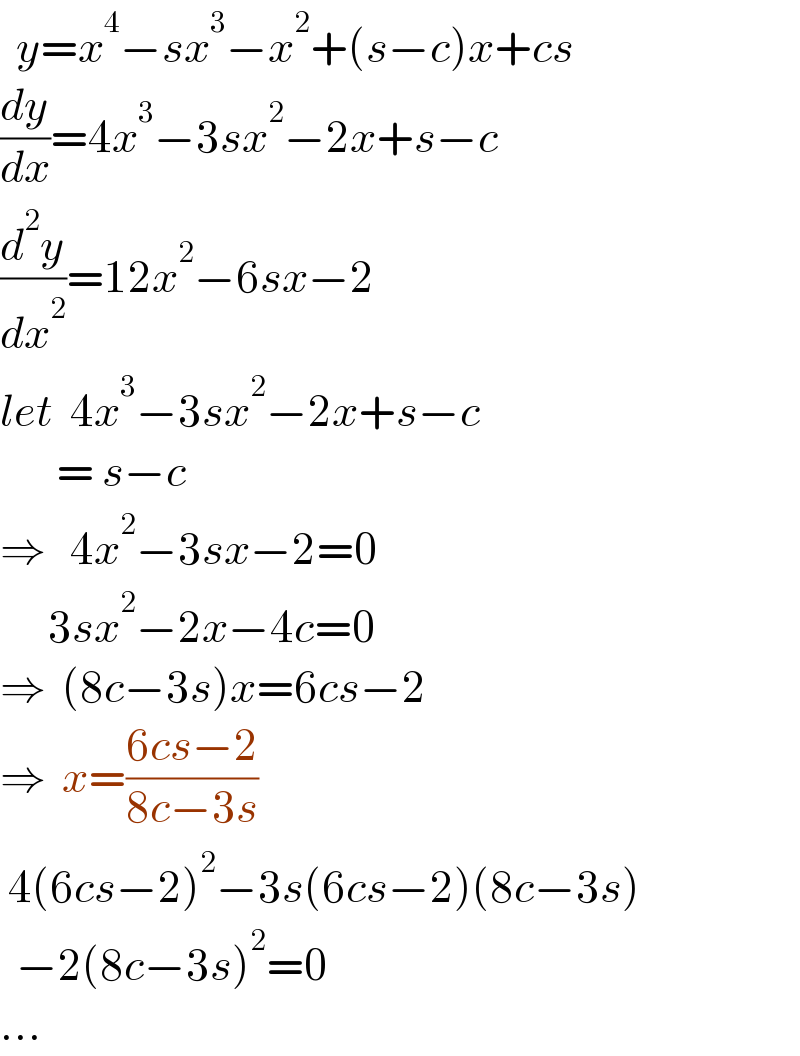
| ||
Question and Answers Forum | ||
Question Number 129832 by ajfour last updated on 19/Jan/21 | ||
 | ||
Commented by ajfour last updated on 19/Jan/21 | ||
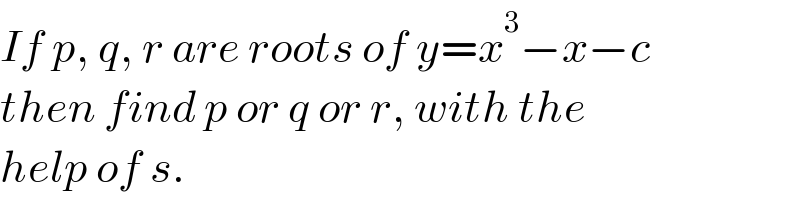 | ||
Commented by MJS_new last updated on 20/Jan/21 | ||
![my opinion: x^4 +ax^2 +bx+c=0 can be solved exactly if we can find exact factors α, β, γ with (x^2 −αx−β)(x^2 +αx−γ)=x^4 +ax^2 +bx+c ⇔ we must find at least one useable exact solution for y^3 +Py+Q=0 with P=−((a^2 +12c)/3)∧Q=−((2a^3 −72ac+27b^2 )/(27)) now what you seem to want is finding s in order to solve the following: (X^3 −X−C)(X−s)=0 ⇔ X^4 −sX^3 −X^2 −(C−s)X+Cs=0 ⇔ [X=x+(s/4)] ⇔ x^4 −((3s^2 +8)/8)x^2 −((s^3 −4s+8C)/8)x−((3s(s^3 −16s−64C))/(256))=0 ⇒ we must be able to find a solution of y^3 +Py+Q=0 with P=−((3s^2 +9Cs+1)/3) Q=−((27Cs^3 +18s^2 +27Cs+37C^2 −2)/(27)) try with C=(1/3) I don′t think you can find a fitting s following this path without solving another 3^(rd) degree polynome](Q129861.png) | ||
Answered by ajfour last updated on 20/Jan/21 | ||
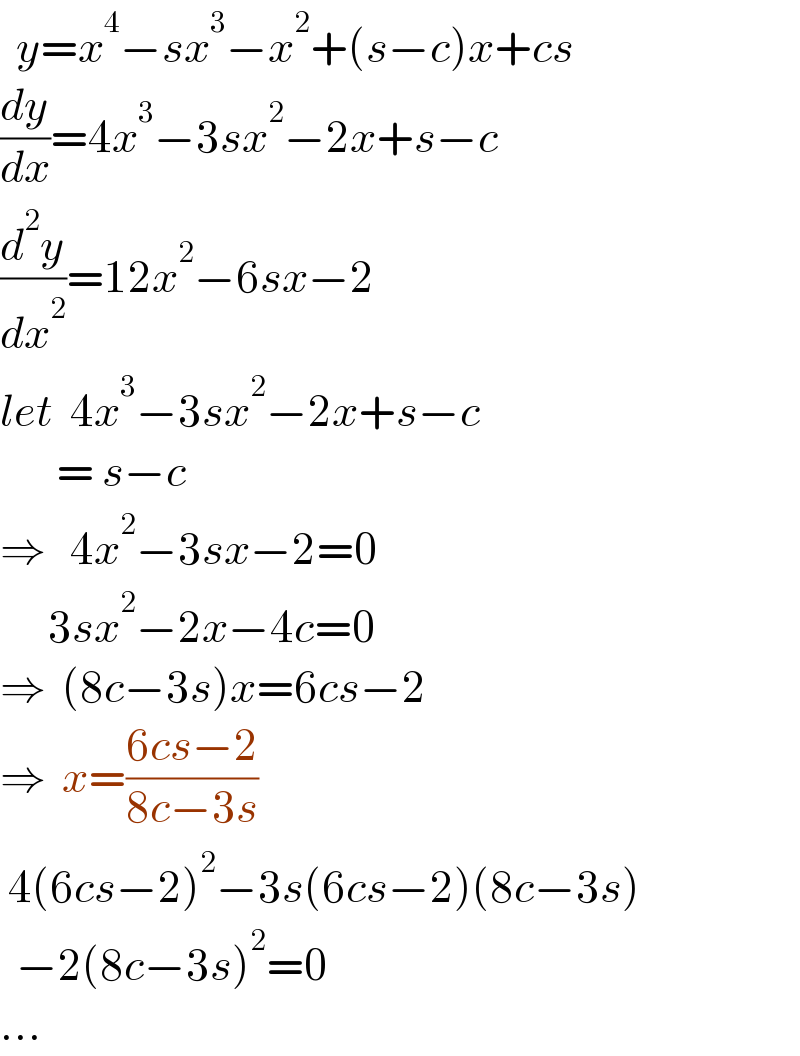 | ||
| ||