Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 129938 by stelor last updated on 21/Jan/21

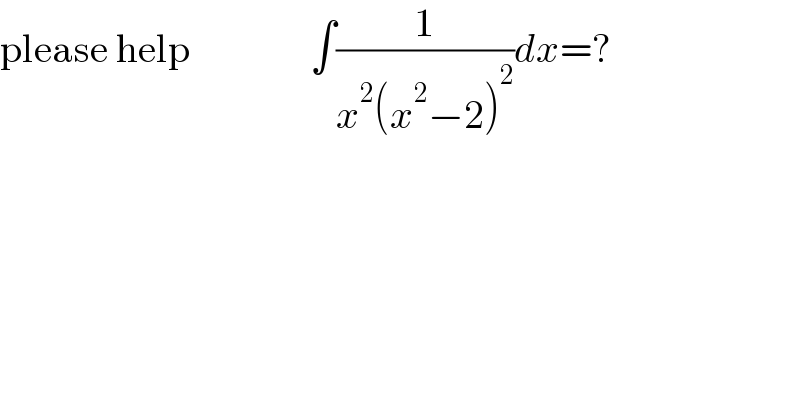
please help ∫(1/(x^2 (x^2 −2)^2 ))dx=?

$$\mathrm{please}\:\mathrm{help}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} }{dx}=? \\ $$$$ \\ $$$$ \\ $$

Answered by Ar Brandon last updated on 21/Jan/21

I=∫(dx/(x^2 (2−x^2 )^2 ))=(1/2)∫(((2−x^2 )+x^2 )/(x^2 (2−x^2 )^2 ))dx=(1/2)∫{(1/(x^2 (2−x^2 )))+(1/((2−x^2 )^2 ))}dx =(1/4)∫(((2−x^2 )+x^2 )/(x^2 (2−x^2 )))dx+(1/2)∫(dx/((2−x^2 )^2 )) =(1/4)∫{(1/x^2 )+(1/(2−x^2 ))}+(1/2)∫(dx/((2−x^2 )^2 )) f(a)=∫(dx/(a^2 −x^2 ))=(1/a)arctanh((x/a)) f ′(a)=−∫((2a)/((a^2 −x^2 )^2 ))dx=(1/a)∙(−(x/a^2 )∙(1/(1−(x^2 /a^2 ))))−(1/a^2 )arctanh((x/a)) ⇒∫(dx/((2−x^2 )^2 ))=−(1/(2(√2)))f ′((√2)) I=(1/4){−(1/x)+(1/( (√2)))tanh^(−1) ((x/( (√2))))}−(1/(4(√2))){(1/( (√2)))∙(x/(x^2 −2))−(1/2)tanh^(−1) ((x/( (√2))))} =(3/(8(√2)))tanh^(−1) ((x/( (√2))))−(1/8)∙(x/(x^2 −2))−(1/(4x))+C

$$\mathcal{I}=\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{2}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left(\mathrm{2}−\mathrm{x}^{\mathrm{2}} \right)+\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} \left(\mathrm{2}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\left\{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{2}−\mathrm{x}^{\mathrm{2}} \right)}+\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\right\}\mathrm{dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\left(\mathrm{2}−\mathrm{x}^{\mathrm{2}} \right)+\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} \left(\mathrm{2}−\mathrm{x}^{\mathrm{2}} \right)}\mathrm{dx}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{dx}}{\left(\mathrm{2}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\int\left\{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}−\mathrm{x}^{\mathrm{2}} }\right\}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{dx}}{\left(\mathrm{2}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\int\frac{\mathrm{dx}}{\mathrm{a}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{a}}\mathrm{arctanh}\left(\frac{\mathrm{x}}{\mathrm{a}}\right) \\ $$$$\mathrm{f}\:'\left(\mathrm{a}\right)=−\int\frac{\mathrm{2a}}{\left(\mathrm{a}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{a}}\centerdot\left(−\frac{\mathrm{x}}{\mathrm{a}^{\mathrm{2}} }\centerdot\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }}\right)−\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\mathrm{arctanh}\left(\frac{\mathrm{x}}{\mathrm{a}}\right) \\ $$$$\Rightarrow\int\frac{\mathrm{dx}}{\left(\mathrm{2}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{f}\:'\left(\sqrt{\mathrm{2}}\right) \\ $$$$\mathcal{I}=\frac{\mathrm{1}}{\mathrm{4}}\left\{−\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{tanh}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\:\sqrt{\mathrm{2}}}\right)\right\}−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\left\{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\centerdot\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tanh}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\:\sqrt{\mathrm{2}}}\right)\right\} \\ $$$$\:\:\:=\frac{\mathrm{3}}{\mathrm{8}\sqrt{\mathrm{2}}}\mathrm{tanh}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\:\sqrt{\mathrm{2}}}\right)−\frac{\mathrm{1}}{\mathrm{8}}\centerdot\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4x}}+\mathcal{C} \\ $$

Commented by stelor last updated on 21/Jan/21

merci−−

$$\mathrm{merci}−− \\ $$

Answered by Ar Brandon last updated on 21/Jan/21

I=∫(dx/(x^2 (x^2 −2)^2 )) , x=(√2)sinθ =∫(((√2)cosθdθ)/(2sin^2 θ∙4(sin^2 θ−1)^2 ))=((√2)/8)∫(dθ/(sin^2 θcos^3 θ)) =((√2)/( 8))∫{(1/(sin^2 θcosθ))+(1/(cos^3 θ))}dθ=((√2)/8)∫{((cosθ)/(sin^2 θ))+(1/(cosθ))+(1/(cos^3 θ))}dθ =((√2)/8){−(1/(sinθ))+ln∣tan((θ/2)+(π/4))∣}+((√2)/( 8))∫(dθ/(cos^3 θ)) ∫(dθ/(cos^3 θ))=∫((cosθ)/(cos^4 θ))dθ=∫((cosθ)/((1−sin^2 θ)^2 ))dθ =∫(du/((1−u^2 )^2 ))=∫(du/(u^4 −2u^2 +1))=(1/2)∫{(((u^2 +1)−(u^2 −1))/(u^4 −2u^2 +1))}du =(1/2)∫{((1+(1/u^2 ))/((u−(1/u))^2 ))−((1−(1/u^2 ))/((u+(1/u))^2 −4))}du =(1/2){∫(dp/p^2 )−∫(dq/(q^2 −4))}=(1/2){−(1/p)+(1/4)ln∣((q+2)/(q−2))∣}+C

$$\mathcal{I}=\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} }\:,\:\mathrm{x}=\sqrt{\mathrm{2}}\mathrm{sin}\theta \\ $$$$\:\:\:=\int\frac{\sqrt{\mathrm{2}}\mathrm{cos}\theta\mathrm{d}\theta}{\mathrm{2sin}^{\mathrm{2}} \theta\centerdot\mathrm{4}\left(\mathrm{sin}^{\mathrm{2}} \theta−\mathrm{1}\right)^{\mathrm{2}} }=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\int\frac{\mathrm{d}\theta}{\mathrm{sin}^{\mathrm{2}} \theta\mathrm{cos}^{\mathrm{3}} \theta} \\ $$$$\:\:\:=\frac{\sqrt{\mathrm{2}}}{\:\mathrm{8}}\int\left\{\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \theta\mathrm{cos}\theta}+\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{3}} \theta}\right\}\mathrm{d}\theta=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\int\left\{\frac{\mathrm{cos}\theta}{\mathrm{sin}^{\mathrm{2}} \theta}+\frac{\mathrm{1}}{\mathrm{cos}\theta}+\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{3}} \theta}\right\}\mathrm{d}\theta \\ $$$$\:\:\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\left\{−\frac{\mathrm{1}}{\mathrm{sin}\theta}+\mathrm{ln}\mid\mathrm{tan}\left(\frac{\theta}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)\mid\right\}+\frac{\sqrt{\mathrm{2}}}{\:\mathrm{8}}\int\frac{\mathrm{d}\theta}{\mathrm{cos}^{\mathrm{3}} \theta} \\ $$$$\int\frac{\mathrm{d}\theta}{\mathrm{cos}^{\mathrm{3}} \theta}=\int\frac{\mathrm{cos}\theta}{\mathrm{cos}^{\mathrm{4}} \theta}\mathrm{d}\theta=\int\frac{\mathrm{cos}\theta}{\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta\right)^{\mathrm{2}} }\mathrm{d}\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\int\frac{\mathrm{du}}{\left(\mathrm{1}−\mathrm{u}^{\mathrm{2}} \right)^{\mathrm{2}} }=\int\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{4}} −\mathrm{2u}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\int\left\{\frac{\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)−\left(\mathrm{u}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{u}^{\mathrm{4}} −\mathrm{2u}^{\mathrm{2}} +\mathrm{1}}\right\}\mathrm{du} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int\left\{\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }}{\left(\mathrm{u}−\frac{\mathrm{1}}{\mathrm{u}}\right)^{\mathrm{2}} }−\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }}{\left(\mathrm{u}+\frac{\mathrm{1}}{\mathrm{u}}\right)^{\mathrm{2}} −\mathrm{4}}\right\}\mathrm{du} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\int\frac{\mathrm{dp}}{\mathrm{p}^{\mathrm{2}} }−\int\frac{\mathrm{dq}}{\mathrm{q}^{\mathrm{2}} −\mathrm{4}}\right\}=\frac{\mathrm{1}}{\mathrm{2}}\left\{−\frac{\mathrm{1}}{\mathrm{p}}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\mid\frac{\mathrm{q}+\mathrm{2}}{\mathrm{q}−\mathrm{2}}\mid\right\}+\mathrm{C} \\ $$

Commented by liberty last updated on 21/Jan/21

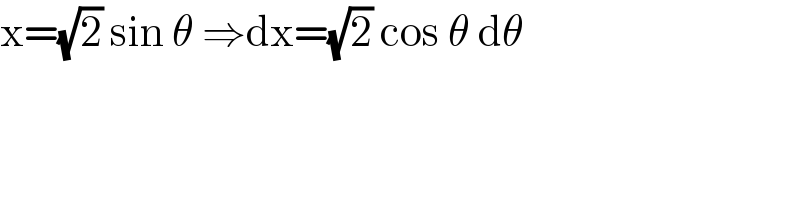
x=(√2) sin θ ⇒dx=(√2) cos θ dθ

$$\mathrm{x}=\sqrt{\mathrm{2}}\:\mathrm{sin}\:\theta\:\Rightarrow\mathrm{dx}=\sqrt{\mathrm{2}}\:\mathrm{cos}\:\theta\:\mathrm{d}\theta \\ $$

Commented by Ar Brandon last updated on 21/Jan/21

Yeah, you're right. Thanks for remark.

Answered by MJS_new last updated on 21/Jan/21

∫(dx/(x^2 (x^2 −2)^2 ))= [Ostrogradski′s Method] =−((3x^2 −4)/(8x(x^2 −2)))−(3/8)∫(dx/(x^2 −2))= =−((3x^2 −4)/(8x(x^2 −2)))−((3(√2))/(32))∫(1/(x+(√2)))−(1/(x−(√2)))dx= =−((3x^2 −4)/(8x(x^2 −2)))−((3(√2))/(32))(ln ∣x+(√2)∣ −ln ∣x−(√2)∣)= =−((3x^2 −4)/(8x(x^2 −2)))−((3(√2))/(32))ln ∣((x+(√2))/(x−(√2)))∣ +C

$$\int\frac{{dx}}{{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=−\frac{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{4}}{\mathrm{8}{x}\left({x}^{\mathrm{2}} −\mathrm{2}\right)}−\frac{\mathrm{3}}{\mathrm{8}}\int\frac{{dx}}{{x}^{\mathrm{2}} −\mathrm{2}}= \\ $$$$=−\frac{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{4}}{\mathrm{8}{x}\left({x}^{\mathrm{2}} −\mathrm{2}\right)}−\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{32}}\int\frac{\mathrm{1}}{{x}+\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{{x}−\sqrt{\mathrm{2}}}{dx}= \\ $$$$=−\frac{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{4}}{\mathrm{8}{x}\left({x}^{\mathrm{2}} −\mathrm{2}\right)}−\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{32}}\left(\mathrm{ln}\:\mid{x}+\sqrt{\mathrm{2}}\mid\:−\mathrm{ln}\:\mid{x}−\sqrt{\mathrm{2}}\mid\right)= \\ $$$$=−\frac{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{4}}{\mathrm{8}{x}\left({x}^{\mathrm{2}} −\mathrm{2}\right)}−\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{32}}\mathrm{ln}\:\mid\frac{{x}+\sqrt{\mathrm{2}}}{{x}−\sqrt{\mathrm{2}}}\mid\:+{C} \\ $$

Answered by mathmax by abdo last updated on 21/Jan/21

I =∫ (dx/(x^2 (x^2 −2)^2 )) ⇒I =∫ (dx/(x^2 (x−(√2))^2 (x+(√2))^2 )) =∫ (dx/(x^2 (((x−(√2))/(x+(√2))))^2 (x+(√2))^4 )) we do the changement ((x−(√2))/(x+(√2)))=t ⇒ x−(√2)=tx+(√2)t ⇒(1−t)x=(√2)+(√2)t ⇒x=(((√2)t+(√2))/(1−t)) ⇒ (dx/dt)=(((√2)(1−t)+(√2)t+(√2))/((1−t)^2 ))=((2(√2))/((1−t)^2 )) and x+(√2)=(((√2)t+(√2))/(1−t))+(√2) =(((√2)t+(√2)+(√2)−(√2)t)/(1−t))=((2(√2))/(1−t)) ⇒ I =∫ ((2(√2))/((1−t)^2 ((((√2)t+(√2))/(1−t)))^2 (((2(√2))/(1−t)))^4 ))dt =(1/((2(√2))^2 ×2)) ∫ (((1−t)^6 )/((1−t)^2 (t+1)^2 ))dt =(1/(16)) ∫ (((t−1)^4 )/((t+1)^2 ))dt =_(t+1=z) (1/(16))∫ (((z−2)^4 )/z^2 )dz =(1/(16))∫ ((Σ_(k=0) ^4 C_4 ^k z^k (−2)^(4−k) )/z^2 )dz =(1/(16)) ∫ (−2)^4 Σ_(k=0) ^4 (−2)^k C_4 ^k z^(k−2) dz =Σ_(k=0 and k≠1) ^4 (−2)^k C_4 ^k (1/(k−1))z^(k−1) −2ln∣z∣ +c =Σ_(k=0) ^4 (((−2)^k C_4 ^k )/(k−1))(t+1)^(k−1) −2ln∣t+1∣+C =Σ_(k=0) ^4 (((−2)^k C_4 ^k )/(k−1))(((x−(√2))/(x+(√2)))+1)^(k−1) −2ln∣((x−(√2))/(3+(√2)))+1∣ +C

$$\mathrm{I}\:=\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} }\:\Rightarrow\mathrm{I}\:=\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}−\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \left(\mathrm{x}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \left(\frac{\mathrm{x}−\sqrt{\mathrm{2}}}{\mathrm{x}+\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \left(\mathrm{x}+\sqrt{\mathrm{2}}\right)^{\mathrm{4}} }\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\frac{\mathrm{x}−\sqrt{\mathrm{2}}}{\mathrm{x}+\sqrt{\mathrm{2}}}=\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{x}−\sqrt{\mathrm{2}}=\mathrm{tx}+\sqrt{\mathrm{2}}\mathrm{t}\:\Rightarrow\left(\mathrm{1}−\mathrm{t}\right)\mathrm{x}=\sqrt{\mathrm{2}}+\sqrt{\mathrm{2}}\mathrm{t}\:\Rightarrow\mathrm{x}=\frac{\sqrt{\mathrm{2}}\mathrm{t}+\sqrt{\mathrm{2}}}{\mathrm{1}−\mathrm{t}}\:\Rightarrow \\ $$$$\frac{\mathrm{dx}}{\mathrm{dt}}=\frac{\sqrt{\mathrm{2}}\left(\mathrm{1}−\mathrm{t}\right)+\sqrt{\mathrm{2}}\mathrm{t}+\sqrt{\mathrm{2}}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }\:\:\mathrm{and}\:\mathrm{x}+\sqrt{\mathrm{2}}=\frac{\sqrt{\mathrm{2}}\mathrm{t}+\sqrt{\mathrm{2}}}{\mathrm{1}−\mathrm{t}}+\sqrt{\mathrm{2}} \\ $$$$=\frac{\sqrt{\mathrm{2}}\mathrm{t}+\sqrt{\mathrm{2}}+\sqrt{\mathrm{2}}−\sqrt{\mathrm{2}}\mathrm{t}}{\mathrm{1}−\mathrm{t}}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{1}−\mathrm{t}}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\:\:\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} \left(\frac{\sqrt{\mathrm{2}}\mathrm{t}+\sqrt{\mathrm{2}}}{\mathrm{1}−\mathrm{t}}\right)^{\mathrm{2}} \left(\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{1}−\mathrm{t}}\right)^{\mathrm{4}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} ×\mathrm{2}}\:\int\:\:\:\frac{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{6}} }{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} \left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\:\int\:\:\frac{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{4}} }{\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dt}\:=_{\mathrm{t}+\mathrm{1}=\mathrm{z}} \:\:\frac{\mathrm{1}}{\mathrm{16}}\int\:\frac{\left(\mathrm{z}−\mathrm{2}\right)^{\mathrm{4}} }{\mathrm{z}^{\mathrm{2}} }\mathrm{dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\int\:\:\frac{\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{4}} \:\mathrm{C}_{\mathrm{4}} ^{\mathrm{k}} \:\mathrm{z}^{\mathrm{k}} \left(−\mathrm{2}\right)^{\mathrm{4}−\mathrm{k}} }{\mathrm{z}^{\mathrm{2}} }\mathrm{dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\:\int\:\:\left(−\mathrm{2}\right)^{\mathrm{4}} \:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{4}} \left(−\mathrm{2}\right)^{\mathrm{k}} \mathrm{C}_{\mathrm{4}} ^{\mathrm{k}} \:\mathrm{z}^{\mathrm{k}−\mathrm{2}} \:\mathrm{dz} \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}\:\mathrm{and}\:\mathrm{k}\neq\mathrm{1}} ^{\mathrm{4}} \left(−\mathrm{2}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{4}} ^{\mathrm{k}} \frac{\mathrm{1}}{\mathrm{k}−\mathrm{1}}\mathrm{z}^{\mathrm{k}−\mathrm{1}} \:\:−\mathrm{2ln}\mid\mathrm{z}\mid\:+\mathrm{c}\:\:\:\: \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{4}} \:\:\frac{\left(−\mathrm{2}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{4}} ^{\mathrm{k}} }{\mathrm{k}−\mathrm{1}}\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} \:−\mathrm{2ln}\mid\mathrm{t}+\mathrm{1}\mid+\mathrm{C} \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{4}} \:\frac{\left(−\mathrm{2}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{4}} ^{\mathrm{k}} }{\mathrm{k}−\mathrm{1}}\left(\frac{\mathrm{x}−\sqrt{\mathrm{2}}}{\mathrm{x}+\sqrt{\mathrm{2}}}+\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} \:−\mathrm{2ln}\mid\frac{\mathrm{x}−\sqrt{\mathrm{2}}}{\mathrm{3}+\sqrt{\mathrm{2}}}+\mathrm{1}\mid\:+\mathrm{C} \\ $$

Commented by mathmax by abdo last updated on 21/Jan/21

k≠1

$$\mathrm{k}\neq\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com