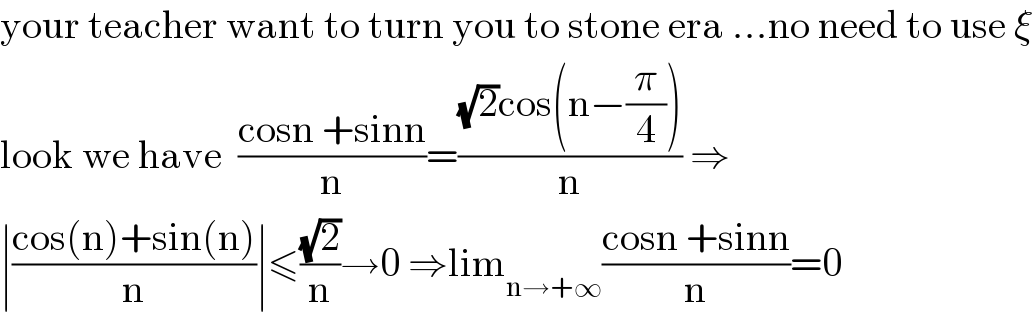Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 129997 by mohammad17 last updated on 21/Jan/21

prove that [(cos(n)+sin(n))/n] converge sequence

$${prove}\:{that}\:\left[\left({cos}\left({n}\right)+{sin}\left({n}\right)\right)/{n}\right]\:{converge}\:{sequence} \\ $$

Answered by Dwaipayan Shikari last updated on 21/Jan/21

Σ_(n=1) ^∞ ((cosn+sinn)/n)=(1/2)Σ_(n=1) ^∞ (e^(in) /n)+(e^(−in) /n)+(1/(2i))Σ_(n=1) ^∞ (e^(in) /n)−(e^(−in) /n) =−(1/2)(log(1−2cos1+1)+log(((1−e^i )/(1−e^(−i) ))) =(1/2)log((1/(4sin^2 (1/2))))+(π/2)−(1/2)=(1/2)(π−1−log(4sin^2 (1/2)))∼1.11

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{cosn}+{sinn}}{{n}}=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{e}^{{in}} }{{n}}+\frac{{e}^{−{in}} }{{n}}+\frac{\mathrm{1}}{\mathrm{2}{i}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{e}^{{in}} }{{n}}−\frac{{e}^{−{in}} }{{n}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left({log}\left(\mathrm{1}−\mathrm{2}{cos}\mathrm{1}+\mathrm{1}\right)+{log}\left(\frac{\mathrm{1}−{e}^{{i}} }{\mathrm{1}−{e}^{−{i}} }\right)\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\frac{\mathrm{1}}{\mathrm{4}{sin}^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}}\right)+\frac{\pi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\pi−\mathrm{1}−{log}\left(\mathrm{4}{sin}^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}\right)\right)\sim\mathrm{1}.\mathrm{11} \\ $$

Commented by mohammad17 last updated on 21/Jan/21

thank you sir but i want this by analyetic function

$${thank}\:{you}\:{sir}\:{but}\:{i}\:{want}\:{this}\:{by}\:{analyetic}\:{function} \\ $$

Answered by mathmax by abdo last updated on 21/Jan/21

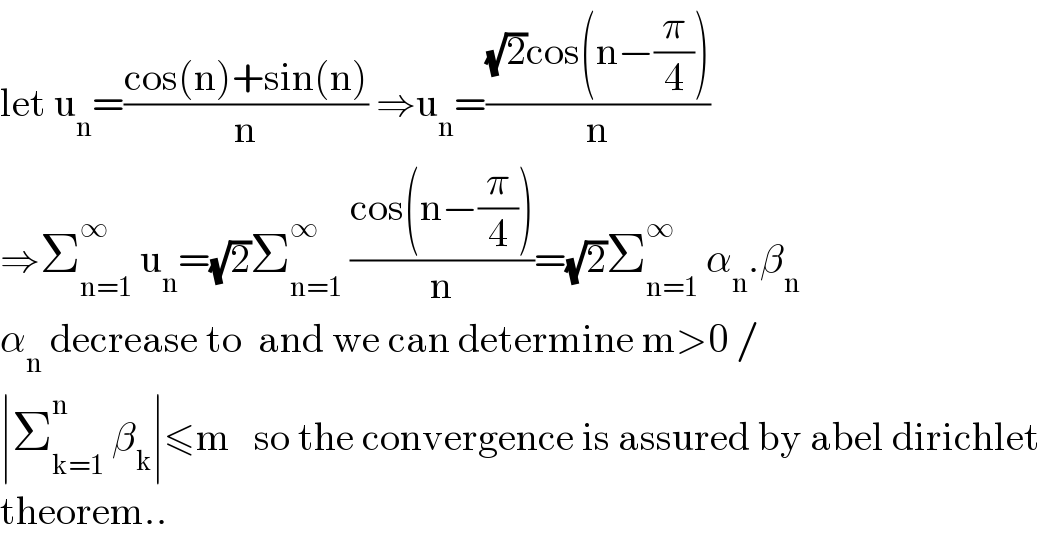
let u_n =((cos(n)+sin(n))/n) ⇒u_n =(((√2)cos(n−(π/4)))/n) ⇒Σ_(n=1) ^∞ u_n =(√2)Σ_(n=1) ^∞ ((cos(n−(π/4)))/n)=(√2)Σ_(n=1) ^∞ α_n .β_n α_n decrease to and we can determine m>0 / ∣Σ_(k=1) ^n β_k ∣≤m so the convergence is assured by abel dirichlet theorem..

$$\mathrm{let}\:\mathrm{u}_{\mathrm{n}} =\frac{\mathrm{cos}\left(\mathrm{n}\right)+\mathrm{sin}\left(\mathrm{n}\right)}{\mathrm{n}}\:\Rightarrow\mathrm{u}_{\mathrm{n}} =\frac{\sqrt{\mathrm{2}}\mathrm{cos}\left(\mathrm{n}−\frac{\pi}{\mathrm{4}}\right)}{\mathrm{n}} \\ $$$$\Rightarrow\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{u}_{\mathrm{n}} =\sqrt{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{n}−\frac{\pi}{\mathrm{4}}\right)}{\mathrm{n}}=\sqrt{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\alpha_{\mathrm{n}} .\beta_{\mathrm{n}} \\ $$$$\alpha_{\mathrm{n}} \:\mathrm{decrease}\:\mathrm{to}\:\:\mathrm{and}\:\mathrm{we}\:\mathrm{can}\:\mathrm{determine}\:\mathrm{m}>\mathrm{0}\:/ \\ $$$$\mid\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\beta_{\mathrm{k}} \mid\leqslant\mathrm{m}\:\:\:\mathrm{so}\:\mathrm{the}\:\mathrm{convergence}\:\mathrm{is}\:\mathrm{assured}\:\mathrm{by}\:\mathrm{abel}\:\mathrm{dirichlet}\: \\ $$$$\mathrm{theorem}.. \\ $$

Commented by mathmax by abdo last updated on 21/Jan/21

α_n decrease to 0

$$\alpha_{\mathrm{n}} \:\mathrm{decrease}\:\mathrm{to}\:\mathrm{0} \\ $$

Commented by mohammad17 last updated on 21/Jan/21

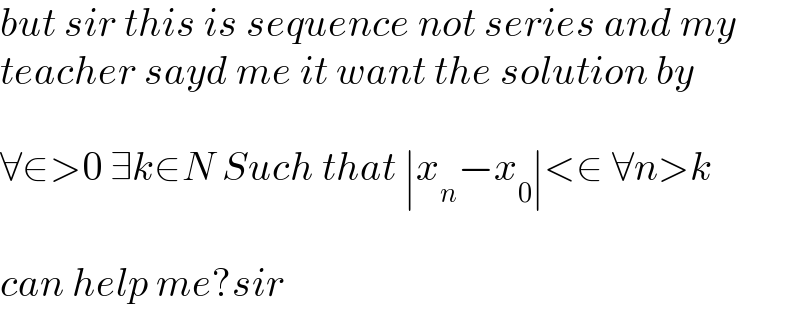
but sir this is sequence not series and my teacher sayd me it want the solution by ∀∈>0 ∃k∈N Such that ∣x_n −x_0 ∣<∈ ∀n>k can help me?sir

$${but}\:{sir}\:{this}\:{is}\:{sequence}\:{not}\:{series}\:{and}\:{my}\: \\ $$$${teacher}\:{sayd}\:{me}\:{it}\:{want}\:{the}\:{solution}\:{by} \\ $$$$ \\ $$$$\forall\in>\mathrm{0}\:\exists{k}\in{N}\:{Such}\:{that}\:\mid{x}_{{n}} −{x}_{\mathrm{0}} \mid<\in\:\forall{n}>{k} \\ $$$$ \\ $$$${can}\:{help}\:{me}?{sir} \\ $$

Commented by mathmax by abdo last updated on 22/Jan/21

your teacher want to turn you to stone era ...no need to use ξ look we have ((cosn +sinn)/n)=(((√2)cos(n−(π/4)))/n) ⇒ ∣((cos(n)+sin(n))/n)∣≤((√2)/n)→0 ⇒lim_(n→+∞) ((cosn +sinn)/n)=0

$$\mathrm{your}\:\mathrm{teacher}\:\mathrm{want}\:\mathrm{to}\:\mathrm{turn}\:\mathrm{you}\:\mathrm{to}\:\mathrm{stone}\:\mathrm{era}\:...\mathrm{no}\:\mathrm{need}\:\mathrm{to}\:\mathrm{use}\:\xi \\ $$$$\mathrm{look}\:\mathrm{we}\:\mathrm{have}\:\:\frac{\mathrm{cosn}\:+\mathrm{sinn}}{\mathrm{n}}=\frac{\sqrt{\mathrm{2}}\mathrm{cos}\left(\mathrm{n}−\frac{\pi}{\mathrm{4}}\right)}{\mathrm{n}}\:\Rightarrow \\ $$$$\mid\frac{\mathrm{cos}\left(\mathrm{n}\right)+\mathrm{sin}\left(\mathrm{n}\right)}{\mathrm{n}}\mid\leqslant\frac{\sqrt{\mathrm{2}}}{\mathrm{n}}\rightarrow\mathrm{0}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \frac{\mathrm{cosn}\:+\mathrm{sinn}}{\mathrm{n}}=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com