
Question and Answers Forum
Question Number 130089 by ajfour last updated on 22/Jan/21
![To solve x^3 =x+c Let y=(x−p)(x^3 −x−c) (dy/dx)=(x^3 −x−c)+(3x^2 −1)(x−p) let (dy/dx)=mx ⇒ (3x^2 −1)(x−p)=mx 3x^3 −3px^2 −(m+1)x+p=0 3(x+c)−3px^2 −(m+1)x+p=0 3px^2 +(m−2)x−(3c+p)=0 and since x^3 =x+c (m−2)x^2 +(2p−3c)x+3cp=0 [9cp^2 +(3c+p)(m−2)]x +[3cp(m−2)+(3c+p)(2p−3c)] =0 x=−(((3c+p)(2p−3c)+3cp(m−2))/(9cp^2 +(3c+p)(m−2))) (m−2)x^2 +(2p−3c)x+(3cp)=0 Now choosing suitable ′p′ value we find ′m′; and then x=f(p,m) ★](Q130089.png)
Commented by bobhans last updated on 22/Jan/21
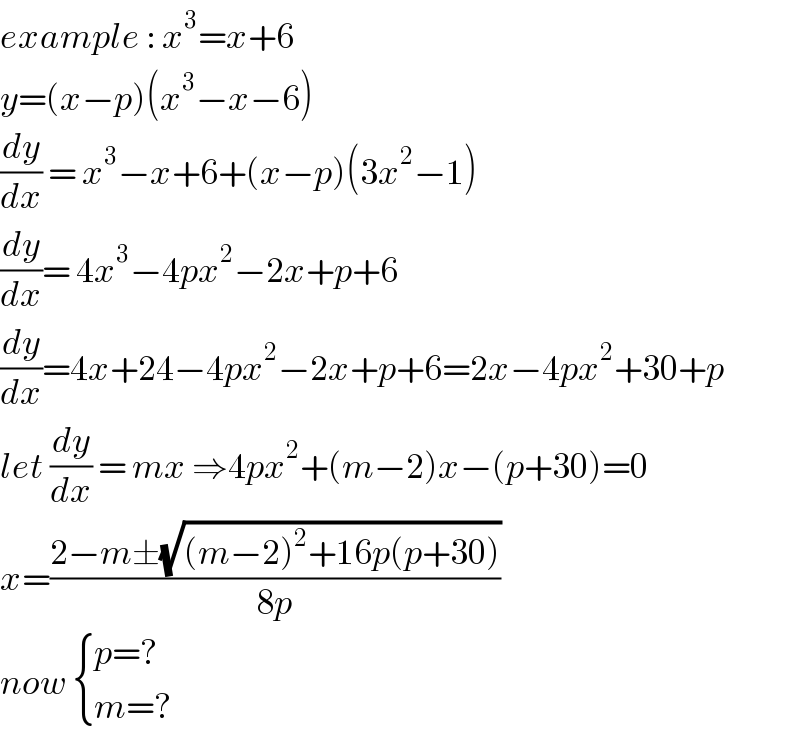
Commented by ajfour last updated on 23/Jan/21
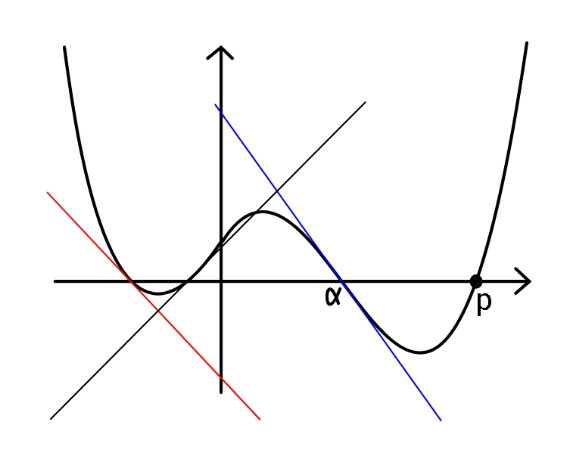
Answered by ajfour last updated on 23/Jan/21
![x=−(((3c+p)(2p−3c)+3cp(m−2))/(9cp^2 +(3c+p)(m−2))) (m−2)x^2 +(2p−3c)x+(3cp)=0 say m−2=M x=−((3cpM+(3c+p)(2p−3c))/((3c+p)M+9cp^2 )) let (M/p)=s , (1/p)=q x=−((3cs+(3cq+1)(2−3cq))/((3cq+1)s+9c)) s[3cs+(3cq+1)(2−3cq)]^2 −(2−3cq)[3cs+(3cq+1)(2−3cq)][(3cq+1)s+9c] +3c[(3cq+1)s+9c]^2 =0 9c^2 s^3 +6c(3cq+1)(2−3cq)s^2 +(3cq+1)^2 (2−3cq)^2 s_(−) −6c(3cq+1)s^2 −54c^2 s +9c^2 q(3cq+1)s^2 +81c^3 qs −(3cq+1)^2 (2−3cq)^2 s_(−) −9c(3cq+1)(2−3cq)^2 +3c(3cq+1)^2 s^2 +54c(3cq+1)s +243c^3 =0 ⇒ (9c^2 )s^3 +[6c(3cq+1)(2−3cq) −6c(3cq+1)+9c^2 q(3cq+1) +3c(3cq+1)^2 ]s^2 + [54c^2 +81c^3 q+54c(3cq+1)]s +[−9c(3cq+1)(2−3cq)^2 +243c^3 ]=0 let q=0 ⇒ s^3 +(1/c)s^2 +6((1/c)+1)s −((4/c)−27c)=0 s=−2.54409 , −0.95044 for c=((30)/(19(√(19)))) x=−((3cs+(3cq+1)(2−3cq))/((3cq+1)s+9c)) and for q=0 x=−((3cs+2)/(s+9c)) = right answer is x=1.14708](Q130106.png)
| ||
Question and Answers Forum | ||
Question Number 130089 by ajfour last updated on 22/Jan/21 | ||
![To solve x^3 =x+c Let y=(x−p)(x^3 −x−c) (dy/dx)=(x^3 −x−c)+(3x^2 −1)(x−p) let (dy/dx)=mx ⇒ (3x^2 −1)(x−p)=mx 3x^3 −3px^2 −(m+1)x+p=0 3(x+c)−3px^2 −(m+1)x+p=0 3px^2 +(m−2)x−(3c+p)=0 and since x^3 =x+c (m−2)x^2 +(2p−3c)x+3cp=0 [9cp^2 +(3c+p)(m−2)]x +[3cp(m−2)+(3c+p)(2p−3c)] =0 x=−(((3c+p)(2p−3c)+3cp(m−2))/(9cp^2 +(3c+p)(m−2))) (m−2)x^2 +(2p−3c)x+(3cp)=0 Now choosing suitable ′p′ value we find ′m′; and then x=f(p,m) ★](Q130089.png) | ||
Commented by bobhans last updated on 22/Jan/21 | ||
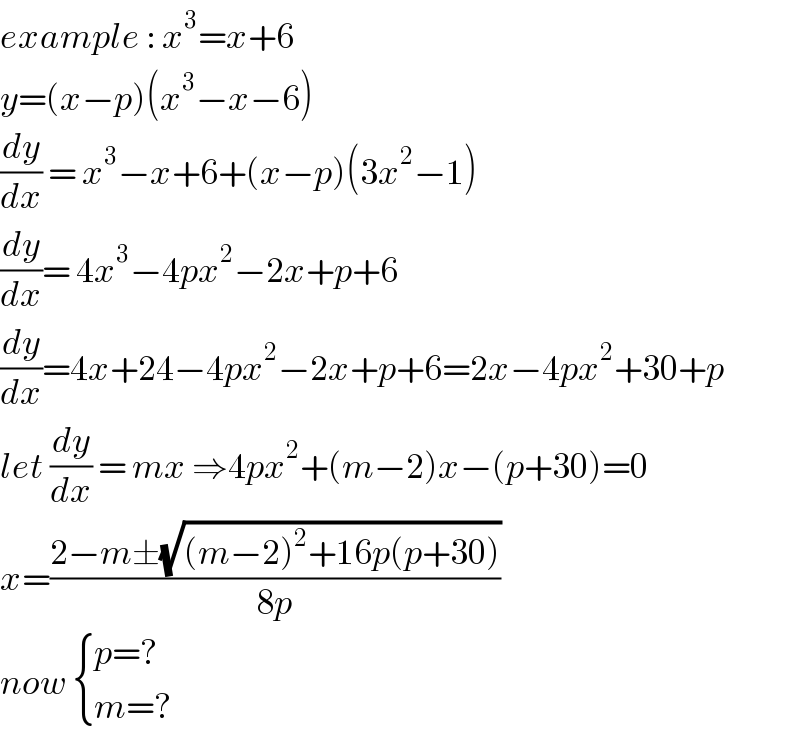 | ||
Commented by ajfour last updated on 23/Jan/21 | ||
 | ||
Answered by ajfour last updated on 23/Jan/21 | ||
![x=−(((3c+p)(2p−3c)+3cp(m−2))/(9cp^2 +(3c+p)(m−2))) (m−2)x^2 +(2p−3c)x+(3cp)=0 say m−2=M x=−((3cpM+(3c+p)(2p−3c))/((3c+p)M+9cp^2 )) let (M/p)=s , (1/p)=q x=−((3cs+(3cq+1)(2−3cq))/((3cq+1)s+9c)) s[3cs+(3cq+1)(2−3cq)]^2 −(2−3cq)[3cs+(3cq+1)(2−3cq)][(3cq+1)s+9c] +3c[(3cq+1)s+9c]^2 =0 9c^2 s^3 +6c(3cq+1)(2−3cq)s^2 +(3cq+1)^2 (2−3cq)^2 s_(−) −6c(3cq+1)s^2 −54c^2 s +9c^2 q(3cq+1)s^2 +81c^3 qs −(3cq+1)^2 (2−3cq)^2 s_(−) −9c(3cq+1)(2−3cq)^2 +3c(3cq+1)^2 s^2 +54c(3cq+1)s +243c^3 =0 ⇒ (9c^2 )s^3 +[6c(3cq+1)(2−3cq) −6c(3cq+1)+9c^2 q(3cq+1) +3c(3cq+1)^2 ]s^2 + [54c^2 +81c^3 q+54c(3cq+1)]s +[−9c(3cq+1)(2−3cq)^2 +243c^3 ]=0 let q=0 ⇒ s^3 +(1/c)s^2 +6((1/c)+1)s −((4/c)−27c)=0 s=−2.54409 , −0.95044 for c=((30)/(19(√(19)))) x=−((3cs+(3cq+1)(2−3cq))/((3cq+1)s+9c)) and for q=0 x=−((3cs+2)/(s+9c)) = right answer is x=1.14708](Q130106.png) | ||
| ||