find the key value [Arg(z)]for (2+i)^(1−i)


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 130104 by mohammad17 last updated on 22/Jan/21

$f i n d t h e k e y v a l u e [A r g (z)] f o r {(2 + i)}^{1 - i}$
	Answered by Olaf last updated on 22/Jan/21

	$z = {(2 + i)}^{1 - i}$ $Z = \ln z = (1 - i) \ln (2 + i)$ $Z = (1 - i) \ln (\sqrt{5} e^{i \arctan \frac{1}{2}})$ $Z = (1 - i) [\frac{1}{2} \ln 5 + i \arctan \frac{1}{2}]$ $Z = (\frac{1}{2} \ln 5 + \arctan \frac{1}{2}) - i (\frac{1}{2} \ln 5 - \arctan \frac{1}{2})$ $z = e^{Z} = \sqrt{5} e^{\arctan \frac{1}{2}} e^{i (\arctan \frac{1}{2} - \frac{1}{2} \ln 5)}$ $Ar g z = \arctan \frac{1}{2} - \frac{1}{2} \ln 5 (+ 2 k π)$ $(or Ar g z = \frac{π - \ln 5}{2} - \arctan 2) (+ 2 k π)$
	Commented by mohammad17 last updated on 22/Jan/21

	$t h a n k y o u s i r b a t h o w b e c a m e l n (2 + i) = l n (\sqrt{5} e^{i a r c t a n \frac{1}{2}})$
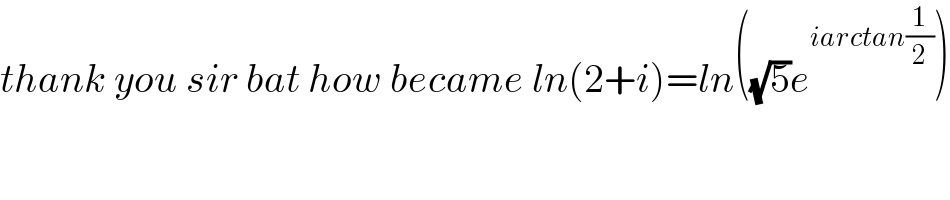
	Commented by Olaf last updated on 22/Jan/21

	$a + i b can be written ρ e^{i θ}$ $ρ = ∣ a + i b ∣ = \sqrt{a^{2} + b^{2}}$ $\tan θ = \frac{b}{a}$ $If a + i b = 2 + i :$ $ρ = ∣ a + i b ∣ = \sqrt{2^{2} + 1} = \sqrt{5}$ $\tan θ = \frac{b}{a} = \frac{1}{2} \Rightarrow θ = \arctan \frac{1}{2}$
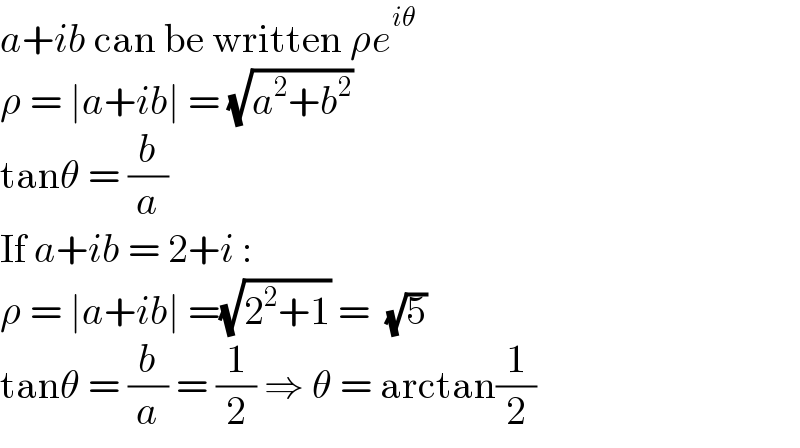
	Commented by mohammad17 last updated on 22/Jan/21

	$t h a n k y o u s i r$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum