
Question and Answers Forum
Question Number 130285 by Lordose last updated on 23/Jan/21
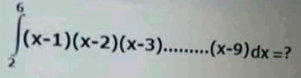
Answered by Olaf last updated on 24/Jan/21
![Ω = ∫_2 ^6 Π_(k=1) ^9 (x−k)dx Let u = x−5 Ω = ∫_(−3) ^(+1) (u+4)...(u+1)u(u−1)...(u−4)du Ω = ∫_(−3) ^(+1) u(u^2 −1)(u^2 −4)(u^2 −9)(u^2 −16)du Ω = ∫_(−3) ^(+1) u(u^4 −5u^2 +4)(u^4 −25u^2 +144)du Ω = ∫_(−3) ^(+1) u(u^8 −30u^6 +273u^4 −820u^2 +576)du Ω = [(u^(10) /(10))−30(u^8 /8)+273(u^6 /6)−820(u^4 /4)+576(u^2 /2)]_(−3) ^(+1) Ω = [(u^(10) /(10))−15(u^8 /4)+91(u^6 /2)−205u^4 +288u^2 ]_(−3) ^(+1) Ω = ((1/(10))−((15)/4)+((91)/2)−205+288) −((3^(10) /(10))−15(3^8 /4)+91(3^6 /2)−205.3^4 +288.9) Ω = ((2497)/(20))−((9153)/(20)) = −((6656)/(20)) = −((1664)/5)](Q130286.png)
Commented by Lordose last updated on 24/Jan/21

| ||
Question and Answers Forum | ||
Question Number 130285 by Lordose last updated on 23/Jan/21 | ||
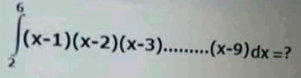 | ||
Answered by Olaf last updated on 24/Jan/21 | ||
![Ω = ∫_2 ^6 Π_(k=1) ^9 (x−k)dx Let u = x−5 Ω = ∫_(−3) ^(+1) (u+4)...(u+1)u(u−1)...(u−4)du Ω = ∫_(−3) ^(+1) u(u^2 −1)(u^2 −4)(u^2 −9)(u^2 −16)du Ω = ∫_(−3) ^(+1) u(u^4 −5u^2 +4)(u^4 −25u^2 +144)du Ω = ∫_(−3) ^(+1) u(u^8 −30u^6 +273u^4 −820u^2 +576)du Ω = [(u^(10) /(10))−30(u^8 /8)+273(u^6 /6)−820(u^4 /4)+576(u^2 /2)]_(−3) ^(+1) Ω = [(u^(10) /(10))−15(u^8 /4)+91(u^6 /2)−205u^4 +288u^2 ]_(−3) ^(+1) Ω = ((1/(10))−((15)/4)+((91)/2)−205+288) −((3^(10) /(10))−15(3^8 /4)+91(3^6 /2)−205.3^4 +288.9) Ω = ((2497)/(20))−((9153)/(20)) = −((6656)/(20)) = −((1664)/5)](Q130286.png) | ||
| ||
Commented by Lordose last updated on 24/Jan/21 | ||
 | ||