Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 130307 by mnjuly1970 last updated on 24/Jan/21

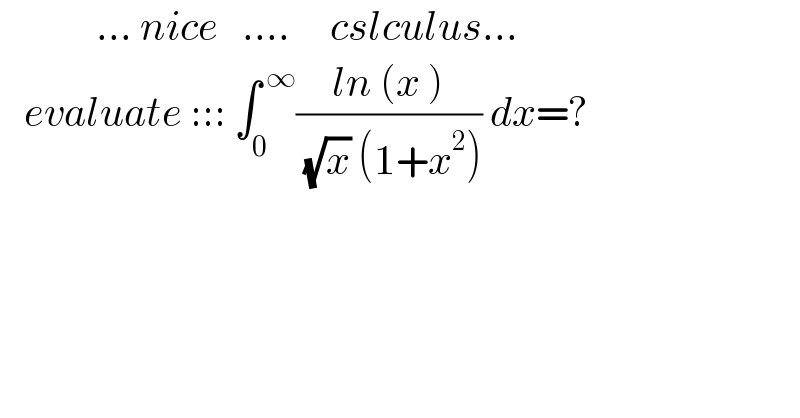
... nice .... cslculus... evaluate ::: ∫_0 ^( ∞) ((ln (x ))/( (√x) (1+x^2 ))) dx=?

$$\:\:\:\:\:\:\:\:\:\:\:\:...\:{nice}\:\:\:....\:\:\:\:\:{cslculus}... \\ $$$$\:\:\:{evaluate}\::::\:\int_{\mathrm{0}} ^{\:\infty} \frac{{ln}\:\left({x}\:\right)}{\:\sqrt{{x}}\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:{dx}=? \\ $$$$ \\ $$

Answered by Dwaipayan Shikari last updated on 24/Jan/21

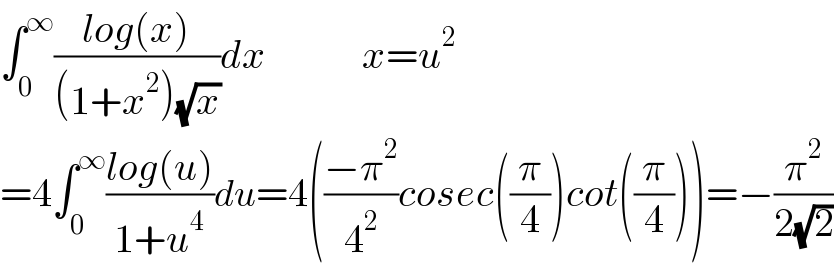
∫_0 ^∞ ((log(x))/((1+x^2 )(√x)))dx x=u^2 =4∫_0 ^∞ ((log(u))/(1+u^4 ))du=4(((−π^2 )/4^2 )cosec((π/4))cot((π/4)))=−(π^2 /(2(√2)))

$$\int_{\mathrm{0}} ^{\infty} \frac{{log}\left({x}\right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\sqrt{{x}}}{dx}\:\:\:\:\:\:\:\:\:\:\:\:{x}={u}^{\mathrm{2}} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\infty} \frac{{log}\left({u}\right)}{\mathrm{1}+{u}^{\mathrm{4}} }{du}=\mathrm{4}\left(\frac{−\pi^{\mathrm{2}} }{\mathrm{4}^{\mathrm{2}} }{cosec}\left(\frac{\pi}{\mathrm{4}}\right){cot}\left(\frac{\pi}{\mathrm{4}}\right)\right)=−\frac{\pi^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$

Commented by Dwaipayan Shikari last updated on 24/Jan/21

Q130137

$${Q}\mathrm{130137} \\ $$

Commented by mnjuly1970 last updated on 24/Jan/21

thank you so much mr dwaypayan.

$${thank}\:{you}\:{so}\:{much}\:{mr}\:{dwaypayan}. \\ $$$$\:\: \\ $$

Answered by mathmax by abdo last updated on 24/Jan/21

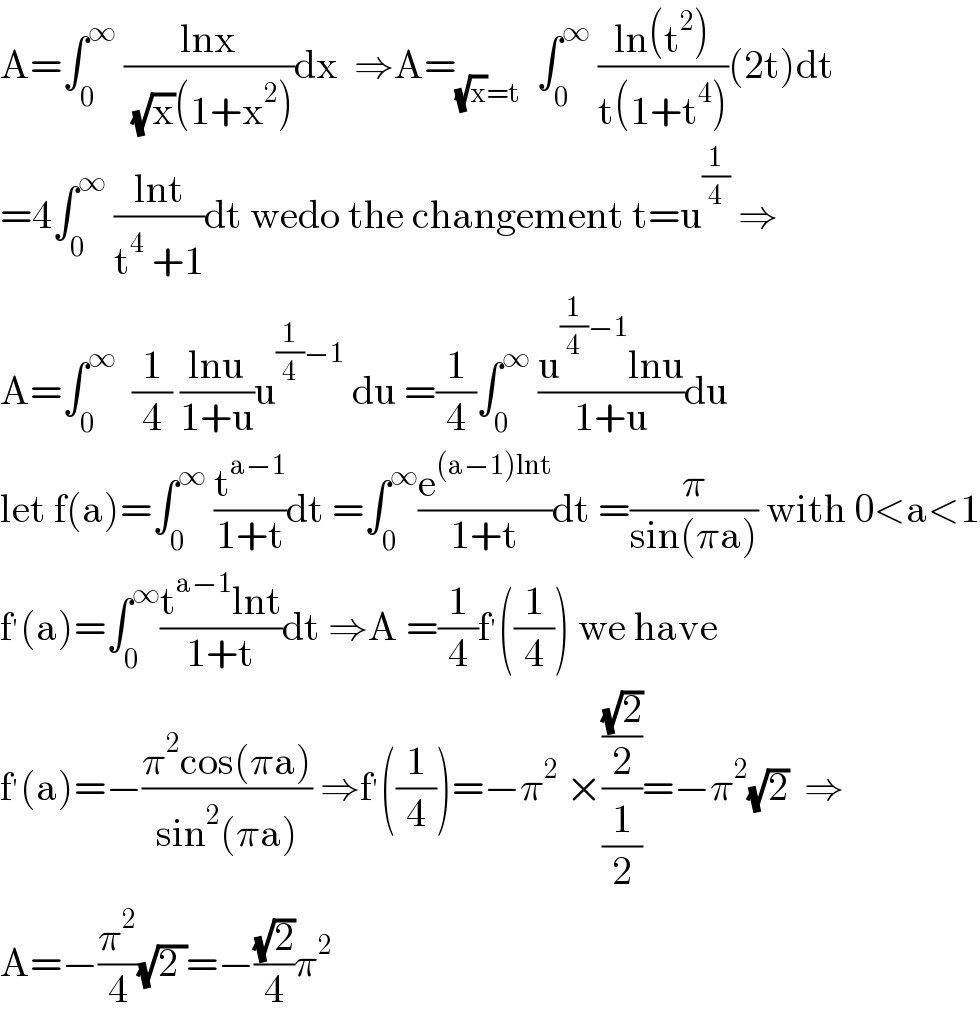
A=∫_0 ^∞ ((lnx)/( (√x)(1+x^2 )))dx ⇒A=_((√x)=t) ∫_0 ^∞ ((ln(t^2 ))/(t(1+t^4 )))(2t)dt =4∫_0 ^∞ ((lnt)/(t^4 +1))dt wedo the changement t=u^(1/4) ⇒ A=∫_0 ^∞ (1/4) ((lnu)/(1+u))u^((1/4)−1) du =(1/4)∫_0 ^∞ ((u^((1/4)−1) lnu)/(1+u))du let f(a)=∫_0 ^∞ (t^(a−1) /(1+t))dt =∫_0 ^∞ (e^((a−1)lnt) /(1+t))dt =(π/(sin(πa))) with 0<a<1 f^′ (a)=∫_0 ^∞ ((t^(a−1) lnt)/(1+t))dt ⇒A =(1/4)f^′ ((1/4)) we have f^′ (a)=−((π^2 cos(πa))/(sin^2 (πa))) ⇒f^′ ((1/4))=−π^2 ×(((√2)/2)/(1/2))=−π^2 (√2) ⇒ A=−(π^2 /4)(√(2 ))=−((√2)/4)π^2

$$\mathrm{A}=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnx}}{\:\sqrt{\mathrm{x}}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\mathrm{dx}\:\:\Rightarrow\mathrm{A}=_{\sqrt{\mathrm{x}}=\mathrm{t}} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} \right)}{\mathrm{t}\left(\mathrm{1}+\mathrm{t}^{\mathrm{4}} \right)}\left(\mathrm{2t}\right)\mathrm{dt} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnt}}{\mathrm{t}^{\mathrm{4}} \:+\mathrm{1}}\mathrm{dt}\:\mathrm{wedo}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{t}=\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{4}}} \:\Rightarrow \\ $$$$\mathrm{A}=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{4}}\:\frac{\mathrm{lnu}}{\mathrm{1}+\mathrm{u}}\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} \:\mathrm{du}\:=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} \mathrm{lnu}}{\mathrm{1}+\mathrm{u}}\mathrm{du} \\ $$$$\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\mathrm{a}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt}\:=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{e}^{\left(\mathrm{a}−\mathrm{1}\right)\mathrm{lnt}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt}\:=\frac{\pi}{\mathrm{sin}\left(\pi\mathrm{a}\right)}\:\mathrm{with}\:\mathrm{0}<\mathrm{a}<\mathrm{1} \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{t}^{\mathrm{a}−\mathrm{1}} \mathrm{lnt}}{\mathrm{1}+\mathrm{t}}\mathrm{dt}\:\Rightarrow\mathrm{A}\:=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{f}^{'} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=−\frac{\pi^{\mathrm{2}} \mathrm{cos}\left(\pi\mathrm{a}\right)}{\mathrm{sin}^{\mathrm{2}} \left(\pi\mathrm{a}\right)}\:\Rightarrow\mathrm{f}^{'} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)=−\pi^{\mathrm{2}} \:×\frac{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}{\frac{\mathrm{1}}{\mathrm{2}}}=−\pi^{\mathrm{2}} \sqrt{\mathrm{2}}\:\:\Rightarrow \\ $$$$\mathrm{A}=−\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\sqrt{\mathrm{2}\:}=−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\pi^{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com