
Question and Answers Forum
Question Number 130392 by mathmax by abdo last updated on 25/Jan/21
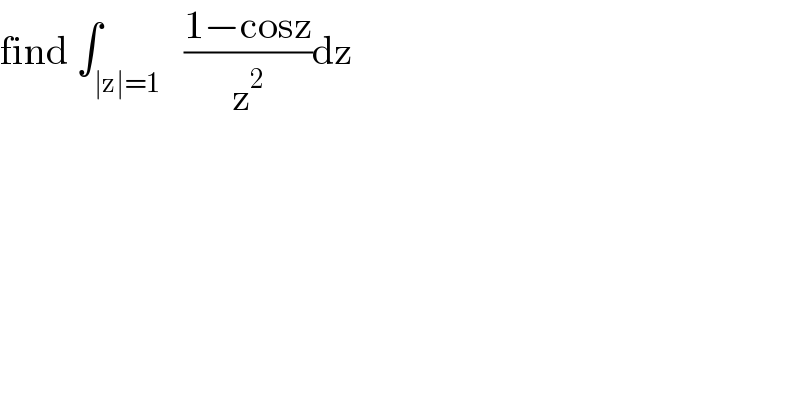
Answered by mohammad17 last updated on 25/Jan/21

Answered by mathmax by abdo last updated on 25/Jan/21
![∫_(∣z∣=1) ((1−cosz)/z^2 )dz =2iπ Res(f,0) with f(z)=((1−cosz)/z^2 ) o is double pole ⇒Res(f,o)=lim_(z→0) (1/((2−1)!)){z^2 f(z)}^((1)) =lim_(z→0) (1−cosz)^((1)) =lim_(z→0) sinz =0 another way ∣z∣=1 ⇒z=e^(iθ) ⇒∫_(∣z∣=1) ((1−cosz)/z^2 ) =∫_0 ^(2π) ((1−cos(e^(iθ) ))/e^(2iθ) )ie^(iθ) dθ =i∫_0 ^(2π) e^(−iθ) (1−cos(e^(iθ) ))dθ =i∫_0 ^(2π) e^(−iθ) dθ−i∫_0 ^(2π) e^(−iθ) cos(e^(iθ) )dθ =0−i∫_0 ^(2π) e^(−iθ) (Σ_(n=0) ^∞ (((−1)^n e^(2inθ) )/((2n)!)))dθ =−iΣ_(n=0) ^∞ (((−1)^n )/(2n!)) ∫_0 ^(2π) e^((2n−1)iθ) dθ =−iΣ_(n=0) ^∞ (((−1)^n )/((2n)!))[(1/((2n−1)))e^((2n−1)iθ) ]_0 ^(2π) =0](Q130464.png)
| ||
Question and Answers Forum | ||
Question Number 130392 by mathmax by abdo last updated on 25/Jan/21 | ||
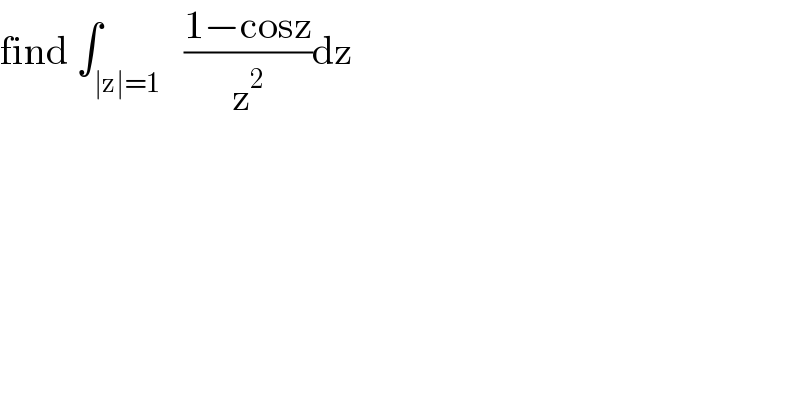 | ||
Answered by mohammad17 last updated on 25/Jan/21 | ||
 | ||
| ||
Answered by mathmax by abdo last updated on 25/Jan/21 | ||
![∫_(∣z∣=1) ((1−cosz)/z^2 )dz =2iπ Res(f,0) with f(z)=((1−cosz)/z^2 ) o is double pole ⇒Res(f,o)=lim_(z→0) (1/((2−1)!)){z^2 f(z)}^((1)) =lim_(z→0) (1−cosz)^((1)) =lim_(z→0) sinz =0 another way ∣z∣=1 ⇒z=e^(iθ) ⇒∫_(∣z∣=1) ((1−cosz)/z^2 ) =∫_0 ^(2π) ((1−cos(e^(iθ) ))/e^(2iθ) )ie^(iθ) dθ =i∫_0 ^(2π) e^(−iθ) (1−cos(e^(iθ) ))dθ =i∫_0 ^(2π) e^(−iθ) dθ−i∫_0 ^(2π) e^(−iθ) cos(e^(iθ) )dθ =0−i∫_0 ^(2π) e^(−iθ) (Σ_(n=0) ^∞ (((−1)^n e^(2inθ) )/((2n)!)))dθ =−iΣ_(n=0) ^∞ (((−1)^n )/(2n!)) ∫_0 ^(2π) e^((2n−1)iθ) dθ =−iΣ_(n=0) ^∞ (((−1)^n )/((2n)!))[(1/((2n−1)))e^((2n−1)iθ) ]_0 ^(2π) =0](Q130464.png) | ||
| ||