
Question and Answers Forum
Question Number 130536 by mathmax by abdo last updated on 26/Jan/21
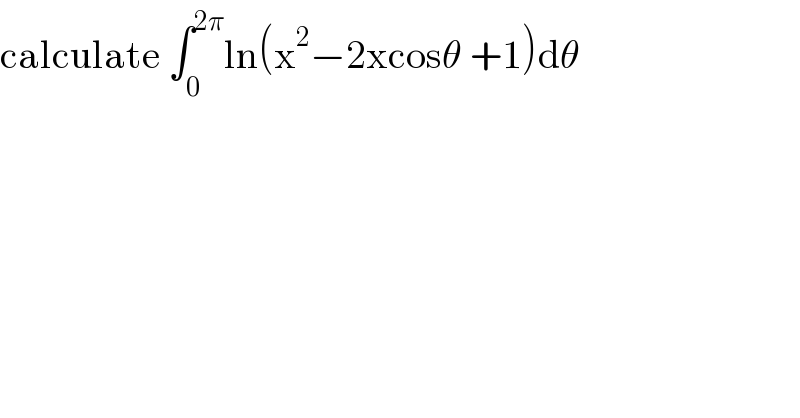
Answered by Ar Brandon last updated on 26/Jan/21
![1. 1−2acos(x)+a^2 =cos^2 −2acos(x)+a^2 +sin^2 (x) =(cos(x)−a)^2 +sin^2 (x)>0 2. 1−2a cos((2kπ)/n)+a^2 =(cos((2kπ)/n)−a)^2 +sin^2 ((2kπ)/n) =(cos((2kπ)/n)−a)^2 −(isin((2kπ)/n))^2 =(cos((2kπ)/n)−isin((2kπ)/n)−a)(cos((2kπ)/n)+isin((2kπ)/n)−a) =(a−e^(2ikπ/n) )(a−e^(−2ikπ/n) ) 3. See Mr 1549442205PVT ′s explanation on Q107498 4. I=∫_0 ^(2π) ln(1−2a cos(x)+a^2 )dx =lim_(n→∞) ((2π)/n)Σ_(k=1) ^n ln(1−2a cos(((2πk)/n))+a^2 ) =lim_(n→∞) ((2π)/n)lnΠ_(k=1) ^n (1−2a cos(((2πk)/n))+a^2 ) =lim_(n→∞) ((2π)/n)ln(a^n −1)^2 =lim_(n→∞) ((4π)/n)ln(a^n −1) =4πlim_(n→∞) [((ln(a^n −1))/n)]=4πlim_(n→∞) [((a^n lna)/(a^n −1))] =4πln(a)](Q130540.png)
Answered by mathmax by abdo last updated on 26/Jan/21

| ||
Question and Answers Forum | ||
Question Number 130536 by mathmax by abdo last updated on 26/Jan/21 | ||
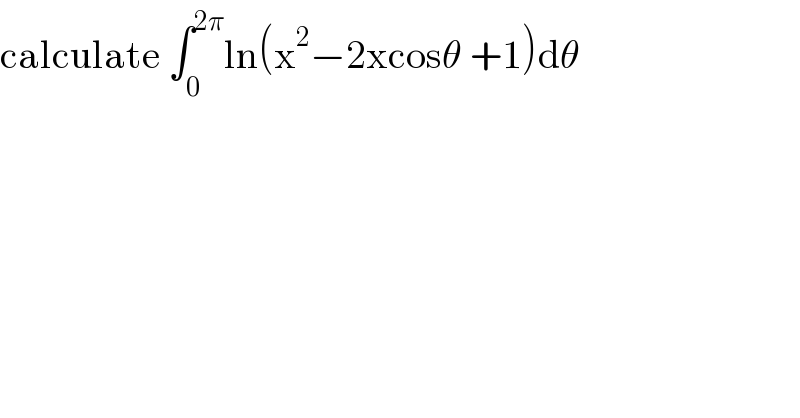 | ||
Answered by Ar Brandon last updated on 26/Jan/21 | ||
![1. 1−2acos(x)+a^2 =cos^2 −2acos(x)+a^2 +sin^2 (x) =(cos(x)−a)^2 +sin^2 (x)>0 2. 1−2a cos((2kπ)/n)+a^2 =(cos((2kπ)/n)−a)^2 +sin^2 ((2kπ)/n) =(cos((2kπ)/n)−a)^2 −(isin((2kπ)/n))^2 =(cos((2kπ)/n)−isin((2kπ)/n)−a)(cos((2kπ)/n)+isin((2kπ)/n)−a) =(a−e^(2ikπ/n) )(a−e^(−2ikπ/n) ) 3. See Mr 1549442205PVT ′s explanation on Q107498 4. I=∫_0 ^(2π) ln(1−2a cos(x)+a^2 )dx =lim_(n→∞) ((2π)/n)Σ_(k=1) ^n ln(1−2a cos(((2πk)/n))+a^2 ) =lim_(n→∞) ((2π)/n)lnΠ_(k=1) ^n (1−2a cos(((2πk)/n))+a^2 ) =lim_(n→∞) ((2π)/n)ln(a^n −1)^2 =lim_(n→∞) ((4π)/n)ln(a^n −1) =4πlim_(n→∞) [((ln(a^n −1))/n)]=4πlim_(n→∞) [((a^n lna)/(a^n −1))] =4πln(a)](Q130540.png) | ||
| ||
Answered by mathmax by abdo last updated on 26/Jan/21 | ||
 | ||
| ||