Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 130616 by bramlexs22 last updated on 27/Jan/21

∫ (dx/(1−k.sin x)) ? where ∣k∣<1

$$\:\int\:\frac{\mathrm{dx}}{\mathrm{1}−\mathrm{k}.\mathrm{sin}\:\mathrm{x}}\:?\:\mathrm{where}\:\mid\mathrm{k}\mid<\mathrm{1} \\ $$

Answered by EDWIN88 last updated on 27/Jan/21

let tan ((x/2))= s ⇒x =2arctan s dx = ((2ds)/(s^2 +1)) ; sin x = 2tan ((x/2))cos^2 ((x/2)) sin x = ((2s)/(1+s^2 )) ; 1−k.sin x=(1−k^2 )+(s−k)^2 (dx/(1−k.sin x)) = ((2ds)/((1−k^2 )+(s−k)^2 )) (dx/(1−k.sin x)) = (2/( (√(1−k^2 )))) .(du/(1+u^2 )) where u = ((s−k)/( (√(1−k^2 )))) I=∫ (2/( (√(1−k^2 )))). (du/(1+u^2 )) I=(2/( (√(1−k^2 )))).arctan (u)+c I=(2/( (√(1−k^2 )))).arctan (((s−k)/( (√(1−k^2 )))))+c I=(2/( (√(1−k^2 )))).arctan (((tan ((x/2))−k)/( (√(1−k^2 )))))+c

$$\:\mathrm{let}\:\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)=\:{s}\:\Rightarrow{x}\:=\mathrm{2arctan}\:{s} \\ $$ $$\:{dx}\:=\:\frac{\mathrm{2}{ds}}{{s}^{\mathrm{2}} +\mathrm{1}}\:;\:\mathrm{sin}\:{x}\:=\:\mathrm{2tan}\:\left(\frac{{x}}{\mathrm{2}}\right)\mathrm{cos}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right) \\ $$ $$\mathrm{sin}\:{x}\:=\:\frac{\mathrm{2}{s}}{\mathrm{1}+{s}^{\mathrm{2}} }\:;\:\mathrm{1}−{k}.\mathrm{sin}\:{x}=\left(\mathrm{1}−{k}^{\mathrm{2}} \right)+\left({s}−{k}\right)^{\mathrm{2}} \\ $$ $$\frac{{dx}}{\mathrm{1}−{k}.\mathrm{sin}\:{x}}\:=\:\frac{\mathrm{2}{ds}}{\left(\mathrm{1}−{k}^{\mathrm{2}} \right)+\left({s}−{k}\right)^{\mathrm{2}} } \\ $$ $$\frac{{dx}}{\mathrm{1}−{k}.\mathrm{sin}\:{x}}\:=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{k}^{\mathrm{2}} }}\:.\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$ $${where}\:{u}\:=\:\frac{{s}−{k}}{\:\sqrt{\mathrm{1}−{k}^{\mathrm{2}} }} \\ $$ $${I}=\int\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{k}^{\mathrm{2}} }}.\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$ $${I}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{k}^{\mathrm{2}} }}.\mathrm{arctan}\:\left({u}\right)+{c} \\ $$ $${I}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{k}^{\mathrm{2}} }}.\mathrm{arctan}\:\left(\frac{{s}−{k}}{\:\sqrt{\mathrm{1}−{k}^{\mathrm{2}} }}\right)+{c} \\ $$ $${I}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{k}^{\mathrm{2}} }}.\mathrm{arctan}\:\left(\frac{\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)−{k}}{\:\sqrt{\mathrm{1}−{k}^{\mathrm{2}} }}\right)+{c}\: \\ $$ $$\: \\ $$

Answered by Dwaipayan Shikari last updated on 27/Jan/21

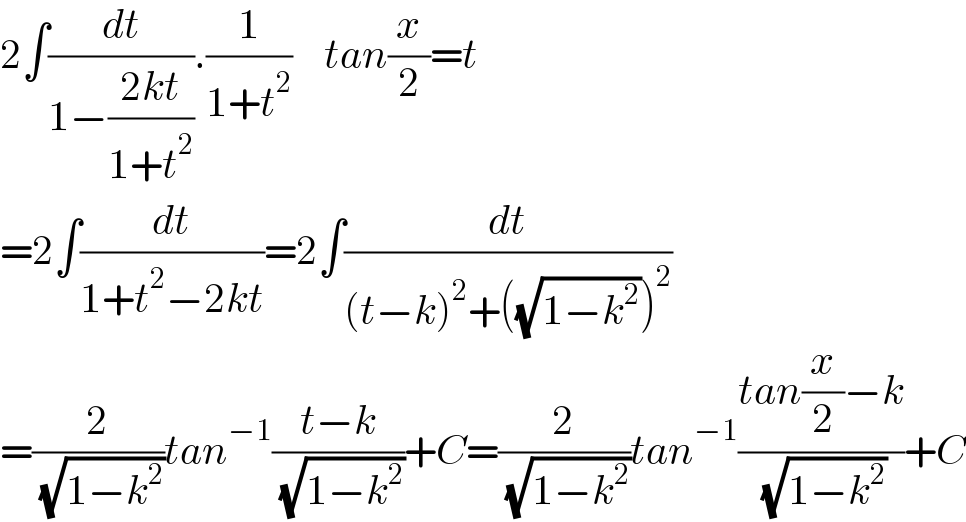
2∫(dt/(1−((2kt)/(1+t^2 )))).(1/(1+t^2 )) tan(x/2)=t =2∫(dt/(1+t^2 −2kt))=2∫(dt/((t−k)^2 +((√(1−k^2 )))^2 )) =(2/( (√(1−k^2 ))))tan^(−1) ((t−k)/( (√(1−k^2 ))))+C=(2/( (√(1−k^2 ))))tan^(−1) ((tan(x/2)−k)/( (√(1−k^2 ))))+C

$$\mathrm{2}\int\frac{{dt}}{\mathrm{1}−\frac{\mathrm{2}{kt}}{\mathrm{1}+{t}^{\mathrm{2}} }}.\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\:\:\:{tan}\frac{{x}}{\mathrm{2}}={t} \\ $$ $$=\mathrm{2}\int\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} −\mathrm{2}{kt}}=\mathrm{2}\int\frac{{dt}}{\left({t}−{k}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{1}−{k}^{\mathrm{2}} }\right)^{\mathrm{2}} } \\ $$ $$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{k}^{\mathrm{2}} }}{tan}^{−\mathrm{1}} \frac{{t}−{k}}{\:\sqrt{\mathrm{1}−{k}^{\mathrm{2}} }}+{C}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{k}^{\mathrm{2}} }}{tan}^{−\mathrm{1}} \frac{{tan}\frac{{x}}{\mathrm{2}}−{k}}{\:\sqrt{\mathrm{1}−{k}^{\mathrm{2}} }}+{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com