Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 130693 by mnjuly1970 last updated on 28/Jan/21

... nice calculus... evaluate :: =∫_0 ^( ∞) ((sin(x))/(e^x −1)) dx =?? ....................

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:...\:{nice}\:\:\:{calculus}... \\ $$$$\:\:\:{evaluate}\::: \\ $$$$\:\:\:\:\:\: =\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}\left({x}\right)}{{e}^{{x}} −\mathrm{1}}\:{dx}\:=?? \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:.................... \\ $$

Answered by mnjuly1970 last updated on 28/Jan/21

∫_0 ^( ∞) ((sin(x))/(e^x −1))dx=(1/(2i))∫_0 ^( ∞) ((e^(ix) −e^(−ix) )/(e^x −1))dx =(1/(2i))∫_0 ^( ∞) ((e^(ix−x) −e^(−ix−x) )/(1−e^(−x) )) dx =(1/(2i))∫_0 ^( ∞) {Σ_(n=0) ^∞ e^(ix−x−nx) −e^(−ix−x−nx) }dx =(1/(2i))Σ_(n=0) ^∞ {(e^(x(i−1−n)) /(i−n−1))+(e^(−x(i+1+n)) /(i+1+n))}_0 ^∞ =((−1)/(2i))Σ_(n=0) ^∞ {(1/(i−(n+1)))+(1/(i+(n+1)))} =((−1)/(2i))Σ_(n=1) ^∞ (1/(i−n))+(1/(i+n))=((−1)/(2i))Σ_(n=1) ^∞ ((2i)/(i^2 −n^2 )) =Σ_(n=1) ^∞ (1/(n^2 +1)) =^(⟨upsilon function⟩) ((πcoth(π) −1)/3)

$$\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}\left({x}\right)}{{e}^{{x}} −\mathrm{1}}{dx}=\frac{\mathrm{1}}{\mathrm{2}{i}}\int_{\mathrm{0}} ^{\:\infty} \frac{{e}^{{ix}} −{e}^{−{ix}} }{{e}^{{x}} −\mathrm{1}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\int_{\mathrm{0}} ^{\:\infty} \frac{{e}^{{ix}−{x}} −{e}^{−{ix}−{x}} }{\mathrm{1}−{e}^{−{x}} }\:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\int_{\mathrm{0}} ^{\:\infty} \left\{\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{e}^{{ix}−{x}−{nx}} −{e}^{−{ix}−{x}−{nx}} \right\}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left\{\frac{{e}^{{x}\left({i}−\mathrm{1}−{n}\right)} }{{i}−{n}−\mathrm{1}}+\frac{{e}^{−{x}\left({i}+\mathrm{1}+{n}\right)} }{{i}+\mathrm{1}+{n}}\right\}_{\mathrm{0}} ^{\infty} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}{i}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left\{\frac{\mathrm{1}}{{i}−\left({n}+\mathrm{1}\right)}+\frac{\mathrm{1}}{{i}+\left({n}+\mathrm{1}\right)}\right\} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}{i}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{i}−{n}}+\frac{\mathrm{1}}{{i}+{n}}=\frac{−\mathrm{1}}{\mathrm{2}{i}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}{i}}{{i}^{\mathrm{2}} −{n}^{\mathrm{2}} } \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{1}}\:\overset{\langle{upsilon}\:\:{function}\rangle} {=}\:\:\frac{\pi{coth}\left(\pi\right)\:−\mathrm{1}}{\mathrm{3}}\: \\ $$

Answered by Dwaipayan Shikari last updated on 28/Jan/21

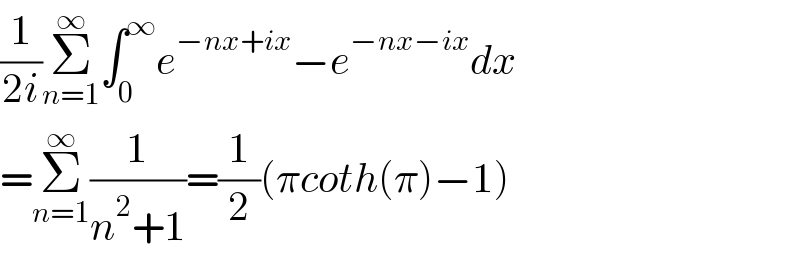
(1/(2i))Σ_(n=1) ^∞ ∫_0 ^∞ e^(−nx+ix) −e^(−nx−ix) dx =Σ_(n=1) ^∞ (1/(n^2 +1))=(1/2)(πcoth(π)−1)

$$\frac{\mathrm{1}}{\mathrm{2}{i}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\infty} {e}^{−{nx}+{ix}} −{e}^{−{nx}−{ix}} {dx} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\pi{coth}\left(\pi\right)−\mathrm{1}\right) \\ $$

Answered by mathmax by abdo last updated on 28/Jan/21

Φ=∫_0 ^∞ ((sinx)/(e^x −1))dx ⇒Φ=∫_0 ^∞ ((e^(−x) sinx)/(1−e^(−x) ))dx =∫_0 ^∞ e^(−x) sinxΣ_(n=0) ^∞ e^(−nx) dx =Σ_(n=0) ^∞ ∫_0 ^∞ e^(−(n+1)x) sinx dx =Σ_(n=0) ^∞ u_n u_n =Im(∫_0 ^∞ e^(−(n+1)x) e^(ix) dx)but ∫_0 ^∞ e^((−(n+1)+i)x) dx =(1/(−(n+1)+i))e^(−(n+1)+i)x) ]_0 ^∞ =(1/(n+1−i)) =((n+1+i)/((n+1)^2 +1)) ⇒u_n =(1/((n+1)^2 +1)) ⇒Φ=Σ_(n=0) ^∞ (1/((n+1)^2 +1)) =Σ_(n=1) ^∞ (1/(n^2 +1)) ,the value of this serie is known see the platform

$$\Phi=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sinx}}{\mathrm{e}^{\mathrm{x}} −\mathrm{1}}\mathrm{dx}\:\Rightarrow\Phi=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{x}} \mathrm{sinx}}{\mathrm{1}−\mathrm{e}^{−\mathrm{x}} }\mathrm{dx}\:\:=\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{x}} \mathrm{sinx}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{nx}} \mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}} \mathrm{sinx}\:\mathrm{dx}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{u}_{\mathrm{n}} \\ $$$$\mathrm{u}_{\mathrm{n}} =\mathrm{Im}\left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}} \mathrm{e}^{\mathrm{ix}} \mathrm{dx}\right)\mathrm{but} \\ $$$$\left.\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\left(−\left(\mathrm{n}+\mathrm{1}\right)+\mathrm{i}\right)\mathrm{x}} \mathrm{dx}\:=\frac{\mathrm{1}}{−\left(\mathrm{n}+\mathrm{1}\right)+\mathrm{i}}\mathrm{e}^{\left.−\left(\mathrm{n}+\mathrm{1}\right)+\mathrm{i}\right)\mathrm{x}} \right]_{\mathrm{0}} ^{\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}−\mathrm{i}}\:=\frac{\mathrm{n}+\mathrm{1}+\mathrm{i}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\mathrm{u}_{\mathrm{n}} =\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\Phi=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} \:+\mathrm{1}}\:,\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{this}\:\mathrm{serie}\:\mathrm{is}\:\mathrm{known}\:\mathrm{see}\:\mathrm{the}\:\mathrm{platform} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com