Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 130759 by mnjuly1970 last updated on 28/Jan/21

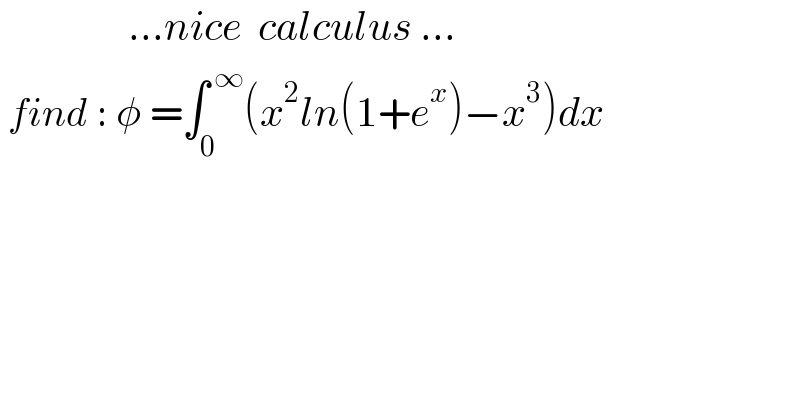
...nice calculus ... find : φ =∫_0 ^( ∞) (x^2 ln(1+e^x )−x^3 )dx

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:...{nice}\:\:{calculus}\:... \\ $$$$\:{find}\::\:\phi\:=\int_{\mathrm{0}} ^{\:\infty} \left({x}^{\mathrm{2}} {ln}\left(\mathrm{1}+{e}^{{x}} \right)−{x}^{\mathrm{3}} \right){dx} \\ $$$$ \\ $$

Answered by mnjuly1970 last updated on 28/Jan/21

ans: φ=∫_0 ^( ∞) x^2 ln(((1+e^x )/e^x ))dx =∫_0 ^( ∞) x^2 ln(1+e^(−x) )dx =Σ_(n=1) ^∞ (−1)^((n−1)) (1/n)∫_0 ^( ∞) x^2 e^(−nx) dx =^(nx=y) Σ_(n=1) ^∞ [(−1)^((n−1)) (1/n^4 )∫_0 ^( ∞) y^2 e^(−y) dy] =Γ(3)Σ_(n=1) ^∞ (((−1)^(n−1) )/n^4 )=2[(1/1^4 )−(1/2^4 )+(1/3^4 )−(1/4^4 )+..] =2 (ζ(4)−(2/2^4 )(ζ(4)))=2((π^4 /(90))−(π^4 /(8∗90))) =(π^4 /(45))(1−(1/8))=(7/8)∗(π^4 /(45))=((7π^4 )/(360)) =... correct or no ???

$${ans}: \\ $$$$\:\:\phi=\int_{\mathrm{0}} ^{\:\infty} {x}^{\mathrm{2}} {ln}\left(\frac{\mathrm{1}+{e}^{{x}} }{{e}^{{x}} }\right){dx} \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\:\infty} {x}^{\mathrm{2}} {ln}\left(\mathrm{1}+{e}^{−{x}} \right){dx} \\ $$$$\:\:\:\:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\left({n}−\mathrm{1}\right)} \frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\:\infty} {x}^{\mathrm{2}} {e}^{−{nx}} {dx} \\ $$$$\:\:\:\:\:\overset{{nx}={y}} {=}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left[\left(−\mathrm{1}\right)^{\left({n}−\mathrm{1}\right)} \frac{\mathrm{1}}{{n}^{\mathrm{4}} }\int_{\mathrm{0}} ^{\:\infty} {y}^{\mathrm{2}} {e}^{−{y}} {dy}\right] \\ $$$$\:\:\:\:\:\:\:=\Gamma\left(\mathrm{3}\right)\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{4}} }=\mathrm{2}\left[\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{4}} }−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{4}} }−\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{4}} }+..\right] \\ $$$$\:\:=\mathrm{2}\:\left(\zeta\left(\mathrm{4}\right)−\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{4}} }\left(\zeta\left(\mathrm{4}\right)\right)\right)=\mathrm{2}\left(\frac{\pi^{\mathrm{4}} }{\mathrm{90}}−\frac{\pi^{\mathrm{4}} }{\mathrm{8}\ast\mathrm{90}}\right) \\ $$$$\:\:=\frac{\pi^{\mathrm{4}} }{\mathrm{45}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{8}}\right)=\frac{\mathrm{7}}{\mathrm{8}}\ast\frac{\pi^{\mathrm{4}} }{\mathrm{45}}=\frac{\mathrm{7}\pi^{\mathrm{4}} }{\mathrm{360}}\:=... \\ $$$$\:\:\:\:\:{correct}\:\:{or}\:\:{no}\:??? \\ $$

Answered by Dwaipayan Shikari last updated on 28/Jan/21

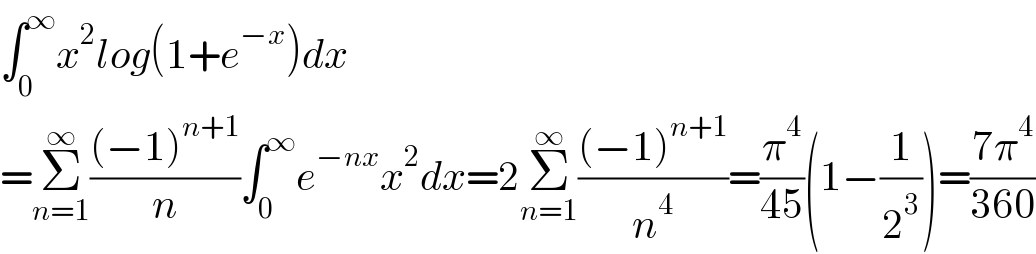
∫_0 ^∞ x^2 log(1+e^(−x) )dx =Σ_(n=1) ^∞ (((−1)^(n+1) )/n)∫_0 ^∞ e^(−nx) x^2 dx=2Σ_(n=1) ^∞ (((−1)^(n+1) )/n^4 )=(π^4 /(45))(1−(1/2^3 ))=((7π^4 )/(360))

$$\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{2}} {log}\left(\mathrm{1}+{e}^{−{x}} \right){dx} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}}\int_{\mathrm{0}} ^{\infty} {e}^{−{nx}} {x}^{\mathrm{2}} {dx}=\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}^{\mathrm{4}} }=\frac{\pi^{\mathrm{4}} }{\mathrm{45}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }\right)=\frac{\mathrm{7}\pi^{\mathrm{4}} }{\mathrm{360}} \\ $$

Commented by mnjuly1970 last updated on 28/Jan/21

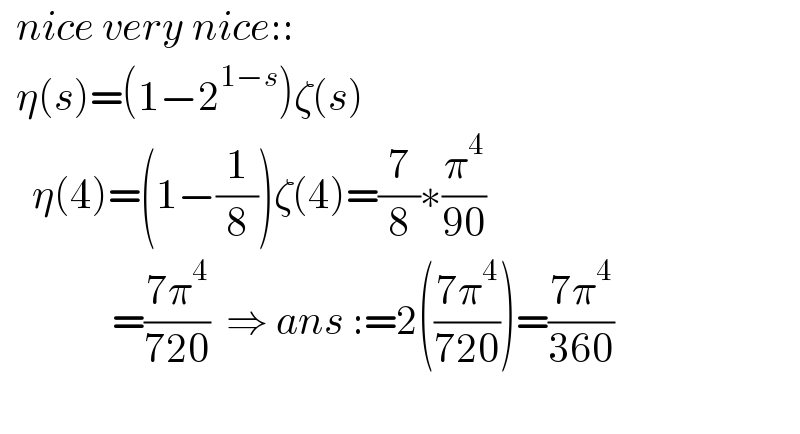
nice very nice:: η(s)=(1−2^(1−s) )ζ(s) η(4)=(1−(1/8))ζ(4)=(7/8)∗(π^4 /(90)) =((7π^4 )/(720)) ⇒ ans :=2(((7π^4 )/(720)))=((7π^4 )/(360))

$$\:\:{nice}\:{very}\:{nice}:: \\ $$$$\:\:\eta\left({s}\right)=\left(\mathrm{1}−\mathrm{2}^{\mathrm{1}−{s}} \right)\zeta\left({s}\right) \\ $$$$\:\:\:\:\eta\left(\mathrm{4}\right)=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{8}}\right)\zeta\left(\mathrm{4}\right)=\frac{\mathrm{7}}{\mathrm{8}}\ast\frac{\pi^{\mathrm{4}} }{\mathrm{90}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{7}\pi^{\mathrm{4}} }{\mathrm{720}}\:\:\Rightarrow\:{ans}\::=\mathrm{2}\left(\frac{\mathrm{7}\pi^{\mathrm{4}} }{\mathrm{720}}\right)=\frac{\mathrm{7}\pi^{\mathrm{4}} }{\mathrm{360}} \\ $$$$ \\ $$

Answered by Lordose last updated on 28/Jan/21

Ω = ∫_0 ^( ∞) (x^2 ln(1+e^x )−x^3 )dx = ∫_0 ^( ∞) x^2 (ln(1+e^(−x) ))dx Ω =^(u=e^(−x) ) ∫_0 ^( 1) (1/u)(−lnu)^2 ln(1+u)du = ∫_0 ^( 1) u^(−1) ln(1+u)ln^2 (u)du Ω = Σ_(n=1) ^∞ (((−1)^(n−1) )/n)∫_0 ^( 1) u^(n−1) ln^2 (u)du Ω(n) = ∫_0 ^( 1) u^n du = (u^(n+1) /(n+1)) = (1/(n+1)) Ω′(n) = ∫_0 ^( 1) u^n ln(u)du = −(1/((n+1)^2 )) Ω′′(n) = ∫_0 ^( 1) u^n ln^2 (u)du = (1/((n+1)^3 )) Ω^(′′) (n−1) = (1/n^3 ) Ω = Σ_(n=1) ^∞ (((−1)^(n−1) )/n^4 ) = ((7π^4 )/(720))

$$ \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\infty} \left(\mathrm{x}^{\mathrm{2}} \mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{\mathrm{x}} \right)−\mathrm{x}^{\mathrm{3}} \right)\mathrm{dx}\:=\:\int_{\mathrm{0}} ^{\:\infty} \mathrm{x}^{\mathrm{2}} \left(\mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{−\mathrm{x}} \right)\right)\mathrm{dx} \\ $$$$\Omega\:\overset{\mathrm{u}=\mathrm{e}^{−\mathrm{x}} } {=}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}}{\mathrm{u}}\left(−\mathrm{lnu}\right)^{\mathrm{2}} \mathrm{ln}\left(\mathrm{1}+\mathrm{u}\right)\mathrm{du}\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{u}^{−\mathrm{1}} \mathrm{ln}\left(\mathrm{1}+\mathrm{u}\right)\mathrm{ln}^{\mathrm{2}} \left(\mathrm{u}\right)\mathrm{du} \\ $$$$\Omega\:=\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{u}^{\mathrm{n}−\mathrm{1}} \mathrm{ln}^{\mathrm{2}} \left(\mathrm{u}\right)\mathrm{du} \\ $$$$\Omega\left(\mathrm{n}\right)\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{u}^{\mathrm{n}} \mathrm{du}\:=\:\frac{\mathrm{u}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\:=\:\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}} \\ $$$$\Omega'\left(\mathrm{n}\right)\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{u}^{\mathrm{n}} \mathrm{ln}\left(\mathrm{u}\right)\mathrm{du}\:=\:−\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Omega''\left(\mathrm{n}\right)\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{u}^{\mathrm{n}} \mathrm{ln}^{\mathrm{2}} \left(\mathrm{u}\right)\mathrm{du}\:=\:\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\Omega^{''} \left(\mathrm{n}−\mathrm{1}\right)\:=\:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} } \\ $$$$\Omega\:=\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}^{\mathrm{4}} }\:=\:\frac{\mathrm{7}\pi^{\mathrm{4}} }{\mathrm{720}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com