Question Number 130994 by mnjuly1970 last updated on 31/Jan/21
$$\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:...\:{advanced}\:\:\:{integral}\:... \\ $$$$\:\:\:\:\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\infty} \left(\frac{{e}^{−{x}} {sin}\left(\mathrm{2}{x}\right)}{{sinh}\left({x}\right)}\right){dx}=? \\ $$$$ \\ $$
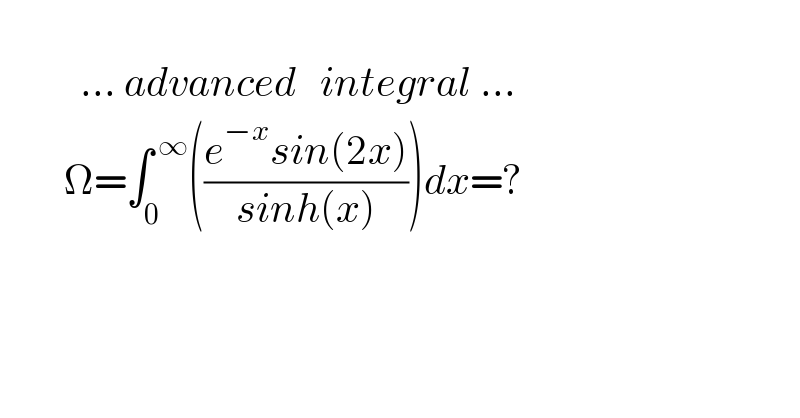
Answered by mindispower last updated on 31/Jan/21
![x→0 sin(2x)=2x+o(x) e^(−x) sin(2x)=2x+o(x),sh(x)=x+o(x) ((e^(−x) sin(2x))/(sh(x)))∼1,integrabl x→∞,sh(x)>1⇒∣((e^(−x) sin(2x))/(sh(x)))∣<e^(−x) ,integrabl ⇒Ω exist and finit sh(x)=((e^(2x) −1)/(2e^x )) Ω=∫((2e^(−2x) sin(2x))/(1−e^(−2x) ))dx=∫_0 ^∞ ((e^(−t) sin(t))/(1−e^(−t) ))dt =Σ_(n≥0) ∫_0 ^∞ e^(−(1+n)t) sin(t)dt =Σ_(n≥0) Im∫_0 ^∞ e^(t(i−(1+n))) dt =Σ_(n≥0) Im[(e^(t(i−(1+n))) /(i−(1+n)))]_0 ^∞ =Σ_(n≥1) Im(((i+(1+n))/(1+n^2 )))=Σ_(n≥0) (1/(1+n^2 ))..done](Q130995.png)
$${x}\rightarrow\mathrm{0} \\ $$$${sin}\left(\mathrm{2}{x}\right)=\mathrm{2}{x}+{o}\left({x}\right) \\ $$$${e}^{−{x}} {sin}\left(\mathrm{2}{x}\right)=\mathrm{2}{x}+{o}\left({x}\right),{sh}\left({x}\right)={x}+{o}\left({x}\right) \\ $$$$\frac{{e}^{−{x}} {sin}\left(\mathrm{2}{x}\right)}{{sh}\left({x}\right)}\sim\mathrm{1},{integrabl}\: \\ $$$${x}\rightarrow\infty,{sh}\left({x}\right)>\mathrm{1}\Rightarrow\mid\frac{{e}^{−{x}} {sin}\left(\mathrm{2}{x}\right)}{{sh}\left({x}\right)}\mid<{e}^{−{x}} ,{integrabl} \\ $$$$\Rightarrow\Omega\:{exist}\:{and}\:{finit} \\ $$$${sh}\left({x}\right)=\frac{{e}^{\mathrm{2}{x}} −\mathrm{1}}{\mathrm{2}{e}^{{x}} } \\ $$$$\Omega=\int\frac{\mathrm{2}{e}^{−\mathrm{2}{x}} {sin}\left(\mathrm{2}{x}\right)}{\mathrm{1}−{e}^{−\mathrm{2}{x}} }{dx}=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{t}} {sin}\left({t}\right)}{\mathrm{1}−{e}^{−{t}} }{dt} \\ $$$$=\underset{{n}\geqslant\mathrm{0}} {\sum}\int_{\mathrm{0}} ^{\infty} {e}^{−\left(\mathrm{1}+{n}\right){t}} {sin}\left({t}\right){dt} \\ $$$$=\underset{{n}\geqslant\mathrm{0}} {\sum}{Im}\int_{\mathrm{0}} ^{\infty} {e}^{{t}\left({i}−\left(\mathrm{1}+{n}\right)\right)} {dt} \\ $$$$=\underset{{n}\geqslant\mathrm{0}} {\sum}{Im}\left[\frac{{e}^{{t}\left({i}−\left(\mathrm{1}+{n}\right)\right)} }{{i}−\left(\mathrm{1}+{n}\right)}\right]_{\mathrm{0}} ^{\infty} \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}{Im}\left(\frac{{i}+\left(\mathrm{1}+{n}\right)}{\mathrm{1}+{n}^{\mathrm{2}} }\right)=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\mathrm{1}+{n}^{\mathrm{2}} }..{done} \\ $$
Commented by mnjuly1970 last updated on 31/Jan/21
$${bravo}\:{bravo}\:{bravo} \\ $$$${mr}\:{power} \\ $$$$\:{extraordinary}... \\ $$
Commented by mnjuly1970 last updated on 31/Jan/21
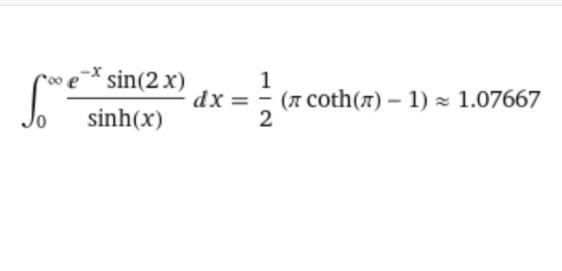
Answered by Dwaipayan Shikari last updated on 31/Jan/21
$$\frac{\mathrm{1}}{{i}}\int_{\mathrm{0}} ^{\infty} \frac{{e}^{\mathrm{2}{ix}} −{e}^{−\mathrm{2}{ix}} }{{e}^{\mathrm{2}{x}} −\mathrm{1}}{dx} \\ $$$$=\frac{\mathrm{1}}{{i}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{nx}+\mathrm{2}{ix}} −{e}^{\mathrm{2}{x}\left({n}+{i}\right)} {dx} \\ $$$$=\frac{\mathrm{1}}{{i}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}\left({n}−{i}\right)}−\frac{\mathrm{1}}{\mathrm{2}\left({n}+{i}\right)}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{1}}=\frac{\pi−\mathrm{1}}{\mathrm{2}}+\frac{\pi}{\mathrm{2}\left({e}^{\mathrm{2}\pi} −\mathrm{1}\right)} \\ $$
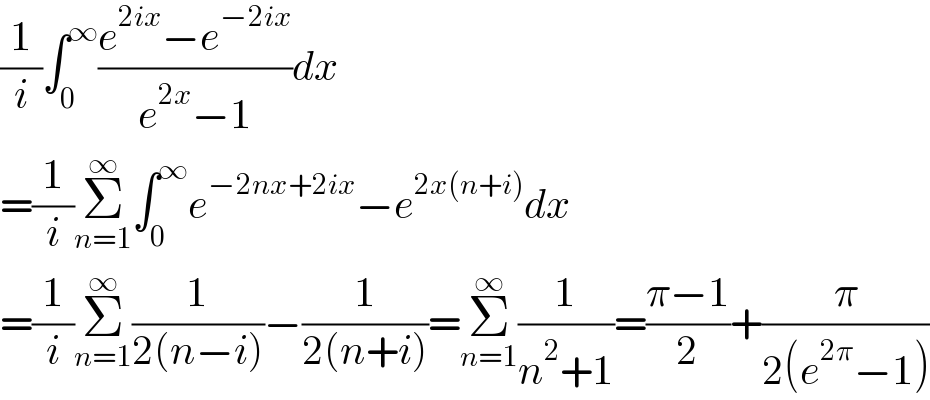
Commented by mnjuly1970 last updated on 31/Jan/21
$${sepas}\:{mr}\:{payan} \\ $$$${tashakor}... \\ $$
Answered by mathmax by abdo last updated on 31/Jan/21
![Φ=∫_0 ^∞ ((e^(−x) sin(2x))/(sh(x)))dx ⇒Φ=2∫_0 ^∞ ((e^(−x) sin(2x))/(e^x −e^(−x) ))dx =2∫_0 ^∞ ((e^(−2x) sin(2x))/(1−e^(−2x) ))dx =_(2x=t) ∫_0 ^∞ ((e^(−t) sint)/(1−e^(−t) ))dt =∫_0 ^∞ e^(−t) sintΣ_(n=0) ^∞ e^(−nt) dt =Σ_(n=0) ^(∞ ) ∫_0 ^∞ e^(−(n+1)t) sint dt but ∫_0 ^∞ e^(−(n+1)t) sint dt =Im(∫_0 ^∞ e^(−(n+1)t+it) dt)and ∫_0 ^∞ e^((−(n+1)+i)t) dt =[(1/(−(n+1)+i))e^((−(n+1)+i)t) ]_0 ^∞ =(1/(n+1−i)) =((n+1+i)/((n+1)^2 +1)) ⇒Φ=Σ_(n=0) ^∞ (1/((n+1)^2 +1))=Σ_(n=1) ^∞ (1/(n^2 +1)) the value of this serie is known](Q130998.png)
$$\Phi=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{x}} \mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{sh}\left(\mathrm{x}\right)}\mathrm{dx}\:\Rightarrow\Phi=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{x}} \mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{e}^{\mathrm{x}} −\mathrm{e}^{−\mathrm{x}} }\mathrm{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{2x}} \mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{1}−\mathrm{e}^{−\mathrm{2x}} }\mathrm{dx}\:=_{\mathrm{2x}=\mathrm{t}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{−\mathrm{t}} \mathrm{sint}}{\mathrm{1}−\mathrm{e}^{−\mathrm{t}} }\mathrm{dt}\: \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{t}} \mathrm{sint}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{nt}} \:\mathrm{dt}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty\:} \int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{t}} \:\mathrm{sint}\:\mathrm{dt}\:\:\:\mathrm{but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{t}} \:\mathrm{sint}\:\mathrm{dt}\:=\mathrm{Im}\left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{t}+\mathrm{it}} \mathrm{dt}\right)\mathrm{and} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\left(−\left(\mathrm{n}+\mathrm{1}\right)+\mathrm{i}\right)\mathrm{t}} \mathrm{dt}\:=\left[\frac{\mathrm{1}}{−\left(\mathrm{n}+\mathrm{1}\right)+\mathrm{i}}\mathrm{e}^{\left(−\left(\mathrm{n}+\mathrm{1}\right)+\mathrm{i}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{\infty} \:=\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}−\mathrm{i}} \\ $$$$=\frac{\mathrm{n}+\mathrm{1}+\mathrm{i}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\Phi=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}}=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{this}\:\mathrm{serie}\:\mathrm{is}\:\mathrm{known} \\ $$
Commented by mnjuly1970 last updated on 31/Jan/21
$${thanks}\:{alot}\:{mr}\:{mathmax}.. \\ $$
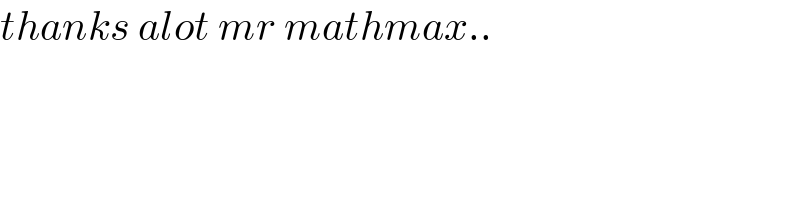
Commented by mathmax by abdo last updated on 31/Jan/21
$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir}. \\ $$
Answered by mnjuly1970 last updated on 31/Jan/21
![note ::∫e^(ax) sin(bx)dx=^(alculus (I) ) ((e^(ax) (asin(bx)−bcos(bx)))/(a^2 +b^2 ))+C Ω=2∫_(0 ) ^( ∞) ((e^(−x) sin(2x))/(e^x −e^(−x) ))=2∫_0 ^( ∞) ((e^(−2x) sin(2x))/(1−e^(−2x) ))dx =2∫_0 ^( ∞) (e^(−2x) sin(2x)Σ_(n=0) ^∞ e^(−2nx) )dx =2Σ_(n=0) ^∞ (∫_0 ^( ∞) sin(2x)e^(−2x(1+n)) dx) =2Σ_(n=0) ^∞ [((e^(−2(1+n)x) (−2(1+n)sin(2x)−2cos(2x)))/(4(1+n)^2 +4))]_0 ^∞ =2Σ_(n=0) ^∞ (2/(4((1+n)^2 +1)))=Σ_(n=1) ^∞ (1/(n^2 +1)) =Σ_(n=1) ^∞ (1/(n^2 +1))=_(function) ^(upsilon) ((πcoth(π)−1)/2) ✓✓](Q131017.png)
$$\:\:\:\:\:{note}\:::\int{e}^{{ax}} {sin}\left({bx}\right){dx}\overset{{alculus}\:\left({I}\right)\:} {=}\frac{{e}^{{ax}} \left({asin}\left({bx}\right)−{bcos}\left({bx}\right)\right)}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+{C} \\ $$$$\:\:\:\:\:\:\:\:\Omega=\mathrm{2}\int_{\mathrm{0}\:} ^{\:\infty} \frac{{e}^{−{x}} {sin}\left(\mathrm{2}{x}\right)}{{e}^{{x}} −{e}^{−{x}} }=\mathrm{2}\int_{\mathrm{0}} ^{\:\infty} \frac{{e}^{−\mathrm{2}{x}} {sin}\left(\mathrm{2}{x}\right)}{\mathrm{1}−{e}^{−\mathrm{2}{x}} }{dx} \\ $$$$\:=\mathrm{2}\int_{\mathrm{0}} ^{\:\infty} \left({e}^{−\mathrm{2}{x}} {sin}\left(\mathrm{2}{x}\right)\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{e}^{−\mathrm{2}{nx}} \right){dx} \\ $$$$=\mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\int_{\mathrm{0}} ^{\:\:\infty} {sin}\left(\mathrm{2}{x}\right){e}^{−\mathrm{2}{x}\left(\mathrm{1}+{n}\right)} {dx}\right) \\ $$$$\:=\mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\frac{{e}^{−\mathrm{2}\left(\mathrm{1}+{n}\right){x}} \left(−\mathrm{2}\left(\mathrm{1}+{n}\right){sin}\left(\mathrm{2}{x}\right)−\mathrm{2}{cos}\left(\mathrm{2}{x}\right)\right)}{\mathrm{4}\left(\mathrm{1}+{n}\right)^{\mathrm{2}} +\mathrm{4}}\right]_{\mathrm{0}} ^{\infty} \\ $$$$=\mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}}{\mathrm{4}\left(\left(\mathrm{1}+{n}\right)^{\mathrm{2}} +\mathrm{1}\right)}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{1}}\underset{{function}} {\overset{{upsilon}} {=}}\frac{\pi{coth}\left(\pi\right)−\mathrm{1}}{\mathrm{2}}\:\:\checkmark\checkmark \\ $$