
Question and Answers Forum
Question Number 131021 by mohammad17 last updated on 31/Jan/21

Answered by Dwaipayan Shikari last updated on 31/Jan/21
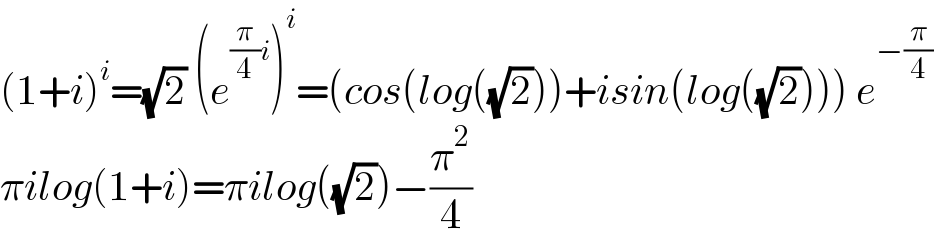
Answered by mr W last updated on 31/Jan/21
![(1) (1+i)=(√2)e^((πi)/4) =e^(ln (√2)+((πi)/4)) (1+i)^i =e^((ln (√2)+((πi)/4))i) =e^(−(π/4)) e^(i ln (√2)) =e^(−(π/4)) [cos (ln (√2))+i sin (ln (√2))] (2) ln (1+i)^(πi) =πi ln [e^(ln (√2)+((πi)/4)) ] =πi(ln (√2)+((πi)/4)) =π(−(π/4)+i ln (√2))](Q131032.png)
| ||
Question and Answers Forum | ||
Question Number 131021 by mohammad17 last updated on 31/Jan/21 | ||
 | ||
Answered by Dwaipayan Shikari last updated on 31/Jan/21 | ||
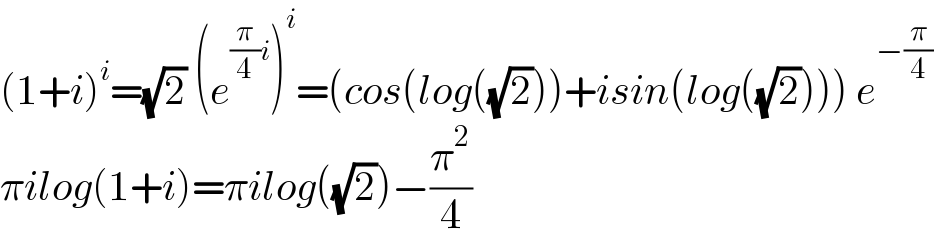 | ||
| ||
Answered by mr W last updated on 31/Jan/21 | ||
![(1) (1+i)=(√2)e^((πi)/4) =e^(ln (√2)+((πi)/4)) (1+i)^i =e^((ln (√2)+((πi)/4))i) =e^(−(π/4)) e^(i ln (√2)) =e^(−(π/4)) [cos (ln (√2))+i sin (ln (√2))] (2) ln (1+i)^(πi) =πi ln [e^(ln (√2)+((πi)/4)) ] =πi(ln (√2)+((πi)/4)) =π(−(π/4)+i ln (√2))](Q131032.png) | ||
| ||