Question Number 131037 by mohammad17 last updated on 31/Jan/21
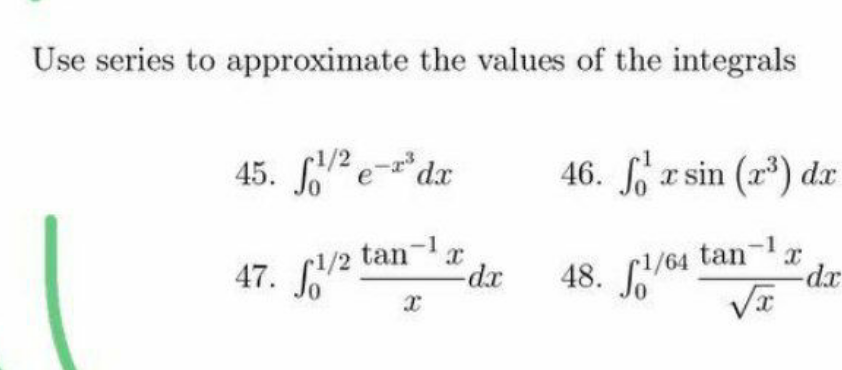
Commented by mathmax by abdo last updated on 31/Jan/21
$$\left.\mathrm{48}\right)\mathrm{use}\:\mathrm{the}\:\mathrm{same}\:\mathrm{method}... \\ $$
Answered by mathmax by abdo last updated on 31/Jan/21
![I=∫_0 ^(1/2) e^(−x^3 ) dx ⇒I =∫_0 ^(1/2) Σ_(n=0) ^∞ (((−x^3 )^n )/(n!))dx =Σ_(n=0) ^∞ (((−1)^n )/(n!))∫_0 ^(1/2) x^(3n) dx =Σ_(n=0) ^∞ (((−1)^n )/(n!))[(1/(3n+1))x^(3n+1) ]_0 ^(1/2) =Σ_(n=0) ^∞ (((−1)^n )/(n!(3n+1)2^(3n+1) )) ⇒I =(1/2)−(1/(4.2^4 ))+(1/(2!.7.2^7 ))−.... you can use 5terms of this serie to get approximate value of I](Q131039.png)
$$\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{e}^{−\mathrm{x}^{\mathrm{3}} } \mathrm{dx}\:\Rightarrow\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{x}^{\mathrm{3}} \right)^{\mathrm{n}} }{\mathrm{n}!}\mathrm{dx}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}!}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{x}^{\mathrm{3n}} \:\mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}!}\left[\frac{\mathrm{1}}{\mathrm{3n}+\mathrm{1}}\mathrm{x}^{\mathrm{3n}+\mathrm{1}} \right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}!\left(\mathrm{3n}+\mathrm{1}\right)\mathrm{2}^{\mathrm{3n}+\mathrm{1}} } \\ $$$$\Rightarrow\mathrm{I}\:=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}.\mathrm{2}^{\mathrm{4}} }+\frac{\mathrm{1}}{\mathrm{2}!.\mathrm{7}.\mathrm{2}^{\mathrm{7}} }−.... \\ $$$$\mathrm{you}\:\mathrm{can}\:\mathrm{use}\:\mathrm{5terms}\:\mathrm{of}\:\mathrm{this}\:\mathrm{serie}\:\mathrm{to}\:\mathrm{get}\:\mathrm{approximate}\:\mathrm{value}\:\mathrm{of}\:\mathrm{I} \\ $$
Commented by mohammad17 last updated on 31/Jan/21
$${thank}\:{you}\:{sir}\:{can}\:{you}\:{help}\:{me}\:{in}\:{all}\:{question}\:{pleas} \\ $$
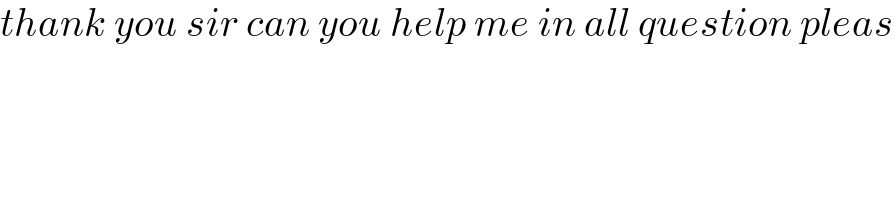
Answered by mathmax by abdo last updated on 31/Jan/21
![J =∫_0 ^1 xsin(x^3 )dx we have sinu =Σ_(n=0) ^∞ (((−1)^n u^(2n+1) )/((2n+1)!)) with radius R=∞ ⇒sin(x^3 ) =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)!))x^(6n+3) ⇒J =∫_0 ^1 xΣ_(n=0) ^∞ (((−1)^n )/((2n+1)!))x^(6n+3) dx =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)!))∫_0 ^1 x^(6n+4) dx =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)!))[(1/(6n+5))x^(6n+5) ]_0 ^1 =Σ_(n0) ^∞ (((−1)^n )/((6n+5)(2n+1)!)) ⇒ J =(1/5)−(1/(11.3!)) +(1/(17.5!))−(1/(23.7!))+... 5 terms give a best approximation of J](Q131041.png)
$$\mathrm{J}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{xsin}\left(\mathrm{x}^{\mathrm{3}} \right)\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{sinu}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{u}^{\mathrm{2n}+\mathrm{1}} }{\left(\mathrm{2n}+\mathrm{1}\right)!}\:\:\mathrm{with}\:\mathrm{radius}\:\mathrm{R}=\infty \\ $$$$\Rightarrow\mathrm{sin}\left(\mathrm{x}^{\mathrm{3}} \right)\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)!}\mathrm{x}^{\mathrm{6n}+\mathrm{3}} \:\Rightarrow\mathrm{J}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)!}\mathrm{x}^{\mathrm{6n}+\mathrm{3}} \:\mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)!}\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{6n}+\mathrm{4}} \:\mathrm{dx}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)!}\left[\frac{\mathrm{1}}{\mathrm{6n}+\mathrm{5}}\mathrm{x}^{\mathrm{6n}+\mathrm{5}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\sum_{\mathrm{n0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{6n}+\mathrm{5}\right)\left(\mathrm{2n}+\mathrm{1}\right)!}\:\Rightarrow \\ $$$$\mathrm{J}\:=\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{11}.\mathrm{3}!}\:+\frac{\mathrm{1}}{\mathrm{17}.\mathrm{5}!}−\frac{\mathrm{1}}{\mathrm{23}.\mathrm{7}!}+... \\ $$$$\mathrm{5}\:\mathrm{terms}\:\mathrm{give}\:\mathrm{a}\:\mathrm{best}\:\mathrm{approximation}\:\mathrm{of}\:\mathrm{J} \\ $$$$ \\ $$
Commented by mohammad17 last updated on 31/Jan/21
$${nice}\:{sir}\:{thank}\:{you} \\ $$
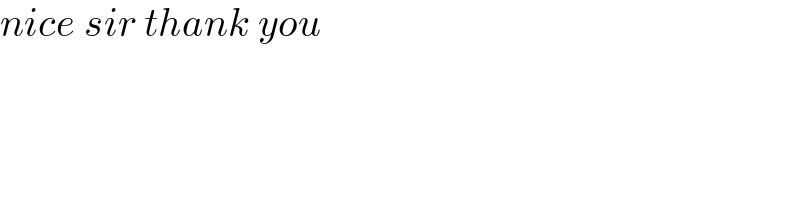
Commented by mathmax by abdo last updated on 31/Jan/21
![another we know u−(u^3 /6)≤sinu ≤u ⇒x^3 −(x^9 /6)≤sin(x^3 )≤x^3 ⇒ x^4 −(x^(10) /6)≤xsin(x^3 )≤x^4 ⇒∫_0 ^1 (x^4 −(x^(10) /6))dx≤∫_0 ^1 xsin(x^3 )dx≤∫_0 ^1 x^4 dx ⇒ [(x^5 /5)−(1/(6.11))x^(11) ]_0 ^1 ≤J≤[(x^5 /5)]_0 ^1 ⇒(1/5)−(1/(6×11))≤J≤(1/5) so v_o =(1/2)((1/5)−(1/(6.11))+(1/5)) =(1/5)−(1/(12.11)) is approximate value of J](Q131043.png)
$$\mathrm{another}\:\mathrm{we}\:\mathrm{know}\:\:\mathrm{u}−\frac{\mathrm{u}^{\mathrm{3}} }{\mathrm{6}}\leqslant\mathrm{sinu}\:\leqslant\mathrm{u}\:\Rightarrow\mathrm{x}^{\mathrm{3}} −\frac{\mathrm{x}^{\mathrm{9}} }{\mathrm{6}}\leqslant\mathrm{sin}\left(\mathrm{x}^{\mathrm{3}} \right)\leqslant\mathrm{x}^{\mathrm{3}} \:\Rightarrow \\ $$$$\mathrm{x}^{\mathrm{4}} −\frac{\mathrm{x}^{\mathrm{10}} }{\mathrm{6}}\leqslant\mathrm{xsin}\left(\mathrm{x}^{\mathrm{3}} \right)\leqslant\mathrm{x}^{\mathrm{4}} \:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{x}^{\mathrm{4}} −\frac{\mathrm{x}^{\mathrm{10}} }{\mathrm{6}}\right)\mathrm{dx}\leqslant\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{xsin}\left(\mathrm{x}^{\mathrm{3}} \right)\mathrm{dx}\leqslant\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{4}} \mathrm{dx}\:\Rightarrow \\ $$$$\left[\frac{\mathrm{x}^{\mathrm{5}} }{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{6}.\mathrm{11}}\mathrm{x}^{\mathrm{11}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:\leqslant\mathrm{J}\leqslant\left[\frac{\mathrm{x}^{\mathrm{5}} }{\mathrm{5}}\right]_{\mathrm{0}} ^{\mathrm{1}} \:\Rightarrow\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{6}×\mathrm{11}}\leqslant\mathrm{J}\leqslant\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\mathrm{so}\:\mathrm{v}_{\mathrm{o}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{6}.\mathrm{11}}+\frac{\mathrm{1}}{\mathrm{5}}\right)\:=\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{12}.\mathrm{11}}\:\mathrm{is}\:\:\mathrm{approximate}\:\mathrm{value}\:\mathrm{of}\:\mathrm{J} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 31/Jan/21
$$\mathrm{you}\:\mathrm{arewelcome}\:\mathrm{sir}. \\ $$
Answered by mathmax by abdo last updated on 31/Jan/21
![K =∫_0 ^(1/2) ((atctanx)/x)dx we have (d/dx)(arctanx)=(1/(1+x^2 )) =Σ_(n=0) ^∞ (−1)^n x^(2n) ⇒ arctanx =Σ_(n=0) ^∞ (((−1)^n )/(2n+1))x^(2n+1) +c (c=0)=Σ_(n=0) ^∞ (((−1)^n )/(2n+1))x^(2n+1) withradius R =1⇒K =∫_0 ^(1/2) Σ_(n=0) ^∞ (((−1)^n )/(2n+1)) x^(2n) dx =Σ_(n=0) ^∞ (((−1)^n )/(2n+1))∫_0 ^(1/2) x^(2n) dx =Σ_(n=0) ^∞ (((−1)^n )/(2n+1))[(1/(2n+1))x^(2n+1) ]_0 ^(1/2) =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^2 .2^(2n+1) )) ⇒ K =(1/2)−(1/(3^2 .2^3 ))+(1/(5^2 .2^5 ))−....](Q131045.png)
$$\mathrm{K}\:=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\frac{\mathrm{atctanx}}{\mathrm{x}}\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{arctanx}\right)=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{2n}} \:\Rightarrow \\ $$$$\mathrm{arctanx}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}+\mathrm{1}}\mathrm{x}^{\mathrm{2n}+\mathrm{1}} \:+\mathrm{c}\:\left(\mathrm{c}=\mathrm{0}\right)=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}+\mathrm{1}}\mathrm{x}^{\mathrm{2n}+\mathrm{1}} \\ $$$$\mathrm{withradius}\:\mathrm{R}\:=\mathrm{1}\Rightarrow\mathrm{K}\:=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}+\mathrm{1}}\:\mathrm{x}^{\mathrm{2n}} \:\mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}+\mathrm{1}}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{x}^{\mathrm{2n}} \mathrm{dx}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}+\mathrm{1}}\left[\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\mathrm{x}^{\mathrm{2n}+\mathrm{1}} \right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} .\mathrm{2}^{\mathrm{2n}+\mathrm{1}} }\:\Rightarrow \\ $$$$\mathrm{K}\:=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} .\mathrm{2}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} .\mathrm{2}^{\mathrm{5}} }−.... \\ $$