
Question Number 131097 by dw last updated on 01/Feb/21
![Determine the value of (S/π), if S is the sum, in radians, all equation solutions contained in the interval [0,14π]. the equation is: cos(x)+cos^5 (x)+cos(7x)=3](Q131097.png)
$${Determine}\:{the}\:{value}\:{of}\:\frac{{S}}{\pi},\:{if}\:{S}\:{is}\:{the}\:{sum},\:{in}\:{radians}, \\ $$$${all}\:{equation}\:{solutions}\:{contained}\:{in}\:{the}\:{interval}\:\left[\mathrm{0},\mathrm{14}\pi\right]. \\ $$$$ \\ $$$${the}\:{equation}\:{is}: \\ $$$${cos}\left({x}\right)+{cos}^{\mathrm{5}} \left({x}\right)+{cos}\left(\mathrm{7}{x}\right)=\mathrm{3} \\ $$
Answered by MJS_new last updated on 01/Feb/21
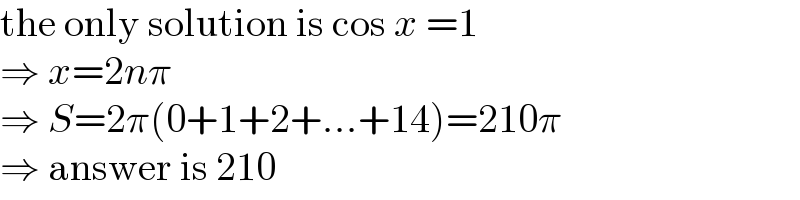
$$\mathrm{the}\:\mathrm{only}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{cos}\:{x}\:=\mathrm{1} \\ $$$$\Rightarrow\:{x}=\mathrm{2}{n}\pi \\ $$$$\Rightarrow\:{S}=\mathrm{2}\pi\left(\mathrm{0}+\mathrm{1}+\mathrm{2}+...+\mathrm{14}\right)=\mathrm{210}\pi \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\mathrm{210} \\ $$
Commented by dw last updated on 01/Feb/21
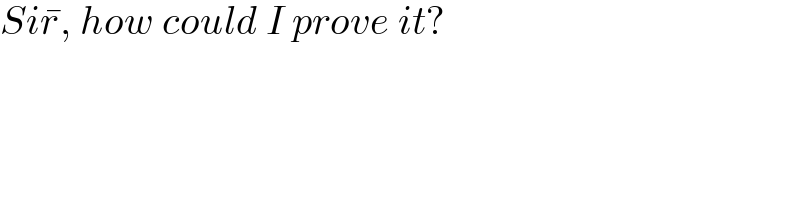
$${Si}\bar {{r}},\:{how}\:{could}\:{I}\:{prove}\:{it}? \\ $$
Commented by dw last updated on 01/Feb/21

$${Thank}\:{you}\:{for}\:{your}\:{solution}. \\ $$
Answered by MJS_new last updated on 01/Feb/21
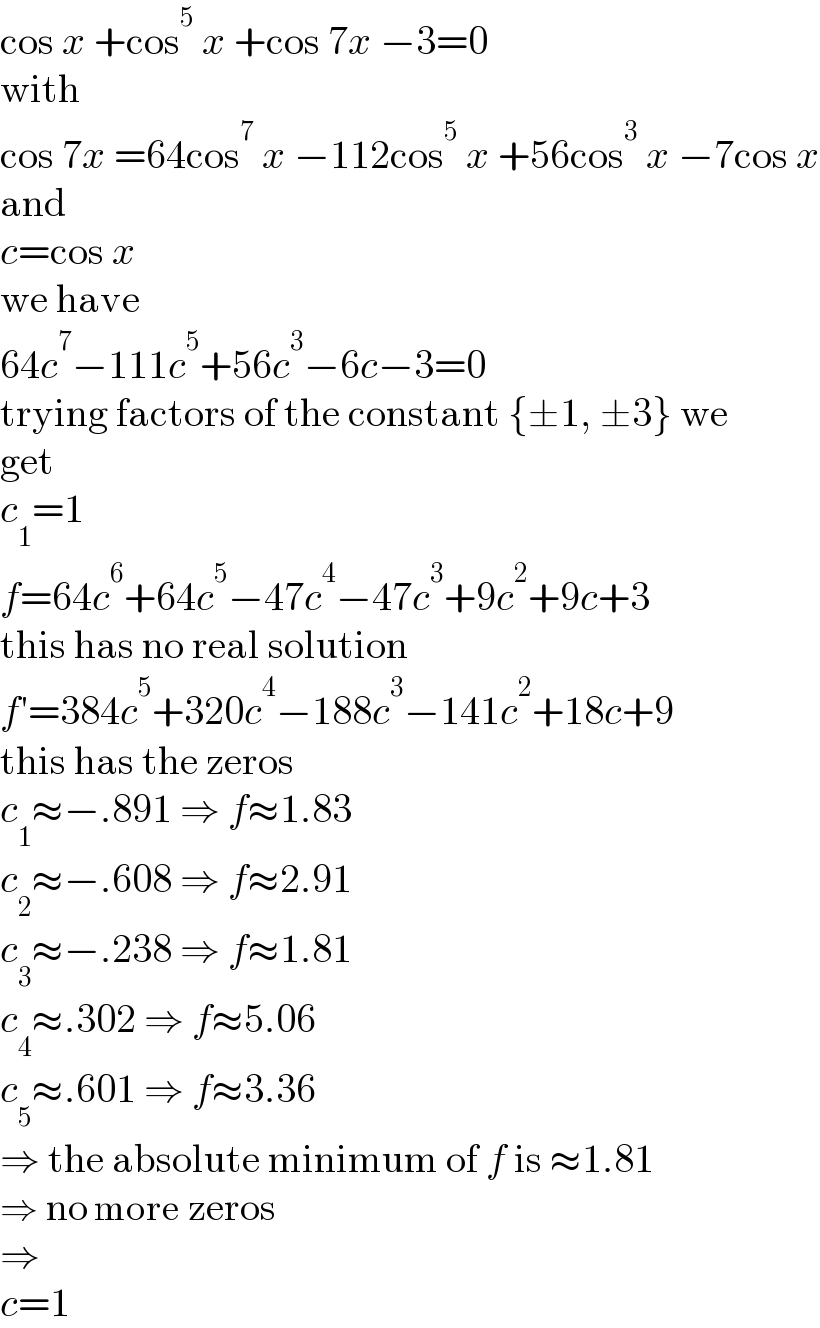
$$\mathrm{cos}\:{x}\:+\mathrm{cos}^{\mathrm{5}} \:{x}\:+\mathrm{cos}\:\mathrm{7}{x}\:−\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{with} \\ $$$$\mathrm{cos}\:\mathrm{7}{x}\:=\mathrm{64cos}^{\mathrm{7}} \:{x}\:−\mathrm{112cos}^{\mathrm{5}} \:{x}\:+\mathrm{56cos}^{\mathrm{3}} \:{x}\:−\mathrm{7cos}\:{x} \\ $$$$\mathrm{and} \\ $$$${c}=\mathrm{cos}\:{x} \\ $$$$\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{64}{c}^{\mathrm{7}} −\mathrm{111}{c}^{\mathrm{5}} +\mathrm{56}{c}^{\mathrm{3}} −\mathrm{6}{c}−\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{trying}\:\mathrm{factors}\:\mathrm{of}\:\mathrm{the}\:\mathrm{constant}\:\left\{\pm\mathrm{1},\:\pm\mathrm{3}\right\}\:\mathrm{we} \\ $$$$\mathrm{get} \\ $$$${c}_{\mathrm{1}} =\mathrm{1} \\ $$$${f}=\mathrm{64}{c}^{\mathrm{6}} +\mathrm{64}{c}^{\mathrm{5}} −\mathrm{47}{c}^{\mathrm{4}} −\mathrm{47}{c}^{\mathrm{3}} +\mathrm{9}{c}^{\mathrm{2}} +\mathrm{9}{c}+\mathrm{3} \\ $$$$\mathrm{this}\:\mathrm{has}\:\mathrm{no}\:\mathrm{real}\:\mathrm{solution} \\ $$$${f}'=\mathrm{384}{c}^{\mathrm{5}} +\mathrm{320}{c}^{\mathrm{4}} −\mathrm{188}{c}^{\mathrm{3}} −\mathrm{141}{c}^{\mathrm{2}} +\mathrm{18}{c}+\mathrm{9} \\ $$$$\mathrm{this}\:\mathrm{has}\:\mathrm{the}\:\mathrm{zeros} \\ $$$${c}_{\mathrm{1}} \approx−.\mathrm{891}\:\Rightarrow\:{f}\approx\mathrm{1}.\mathrm{83} \\ $$$${c}_{\mathrm{2}} \approx−.\mathrm{608}\:\Rightarrow\:{f}\approx\mathrm{2}.\mathrm{91} \\ $$$${c}_{\mathrm{3}} \approx−.\mathrm{238}\:\Rightarrow\:{f}\approx\mathrm{1}.\mathrm{81} \\ $$$${c}_{\mathrm{4}} \approx.\mathrm{302}\:\Rightarrow\:{f}\approx\mathrm{5}.\mathrm{06} \\ $$$${c}_{\mathrm{5}} \approx.\mathrm{601}\:\Rightarrow\:{f}\approx\mathrm{3}.\mathrm{36} \\ $$$$\Rightarrow\:\mathrm{the}\:\mathrm{absolute}\:\mathrm{minimum}\:\mathrm{of}\:{f}\:\mathrm{is}\:\approx\mathrm{1}.\mathrm{81} \\ $$$$\Rightarrow\:\mathrm{no}\:\mathrm{more}\:\mathrm{zeros} \\ $$$$\Rightarrow \\ $$$${c}=\mathrm{1} \\ $$
Commented by dw last updated on 01/Feb/21

$${Thank}\:{you}\:{Sir}!! \\ $$
