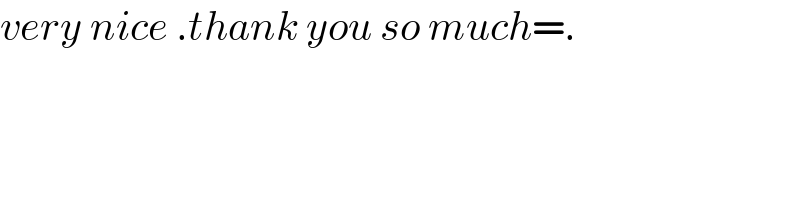Question and Answers Forum
Question Number 131103 by mnjuly1970 last updated on 01/Feb/21
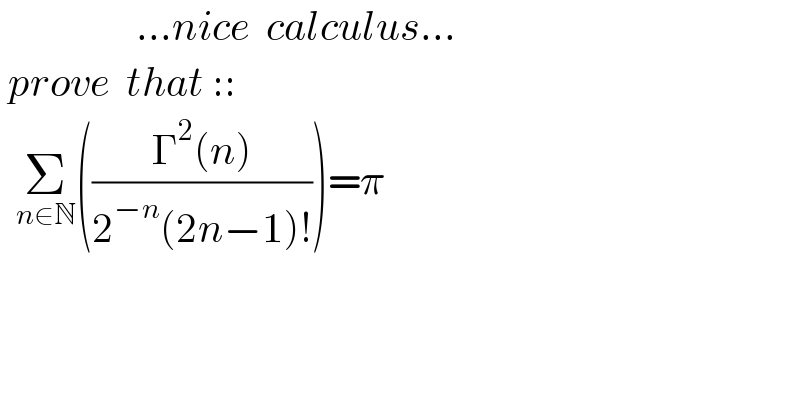
Answered by Ar Brandon last updated on 01/Feb/21
![S=Σ_(n=1) ^∞ ((Γ^2 (n))/(2^(−n) (2n−1)!))=Σ_(n=1) ^∞ ((β(n,n))/2^(−n) ) =Σ_(n=1) ^∞ (1/2^(−n) )∫_0 ^1 x^(n−1) (1−x)^(n−1) dx =∫_0 ^1 {Σ_(n=1) ^∞ 2∙2^(n−1) (x−x^2 )^(n−1) }dx =∫_0 ^1 {2∙(1/(1−(2x−2x^2 )))}dx=∫_0 ^1 ((2dx)/(2x^2 −2x+1)) =∫_0 ^1 (dx/(x^2 −x+(1/2)))=∫_0 ^1 (dx/((x−(1/2))^2 +(1/4))) =2[tan^(−1) (2x−1)]_0 ^1 =2((π/4)+(π/4))=π](Q131114.png)
Commented by mnjuly1970 last updated on 01/Feb/21
Answered by Dwaipayan Shikari last updated on 01/Feb/21
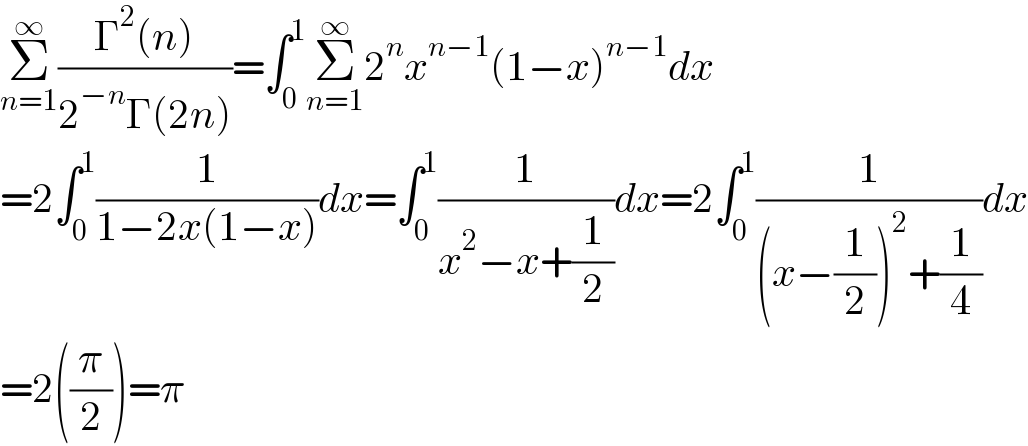
Commented by mnjuly1970 last updated on 01/Feb/21