
Question and Answers Forum
Question Number 131371 by EDWIN88 last updated on 04/Feb/21
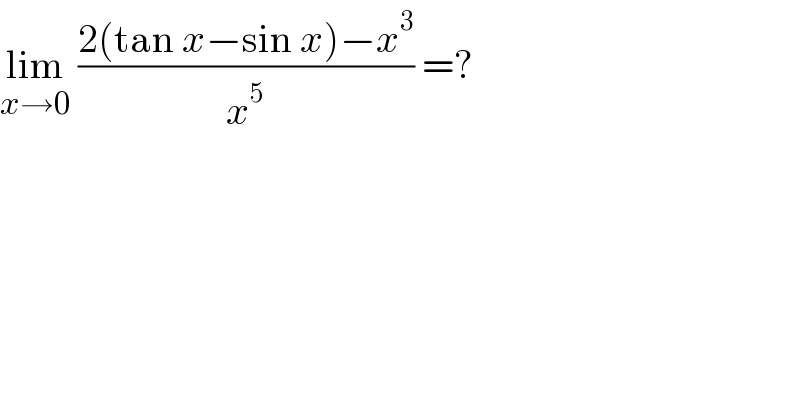
Answered by liberty last updated on 04/Feb/21
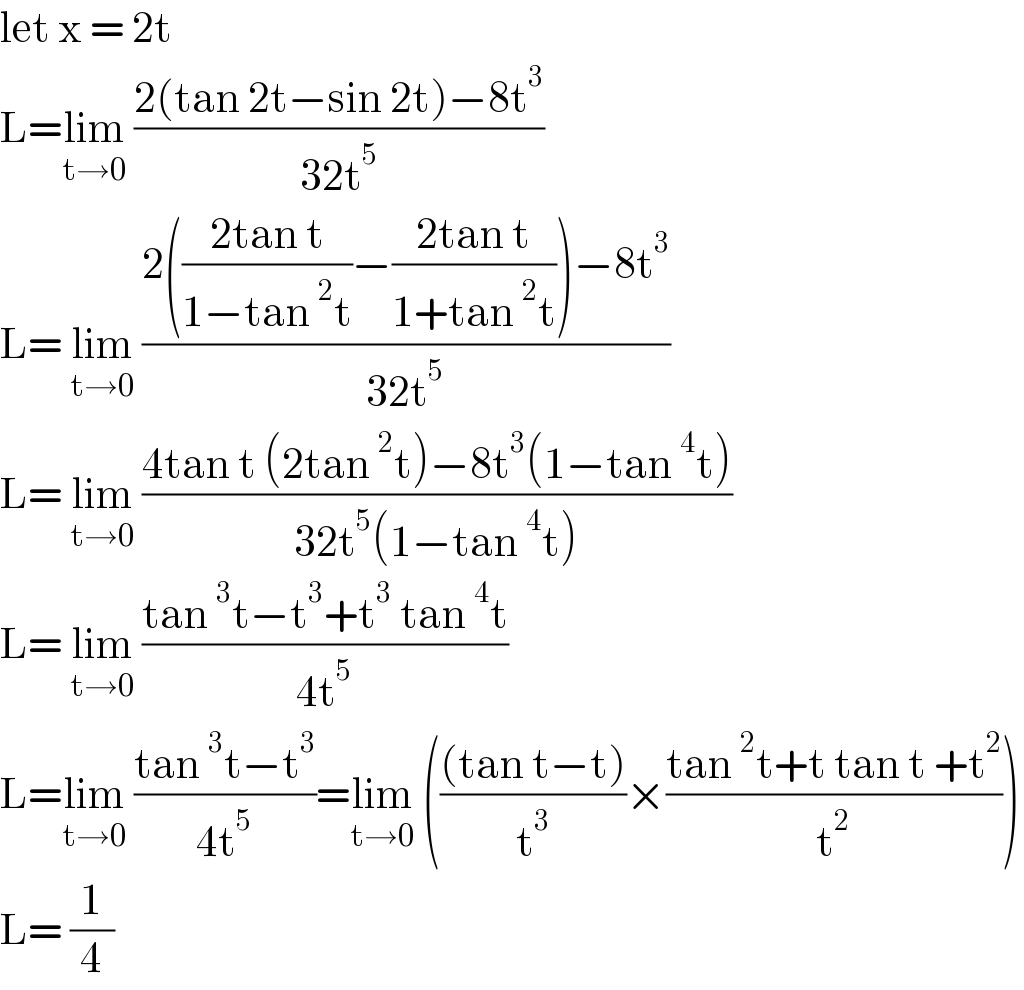
Answered by bemath last updated on 04/Feb/21
![= lim_(x→0) ((2[(x+(x^3 /3)+((2x^5 )/(15)))−(x−(x^3 /6)+(x^5 /(120)))]−x^3 )/x^5 ) = lim_(x→0) ((2((x^3 /2)+((15x^5 )/(120)))−x^3 )/x^5 )=(1/4)](Q131394.png)
| ||
Question and Answers Forum | ||
Question Number 131371 by EDWIN88 last updated on 04/Feb/21 | ||
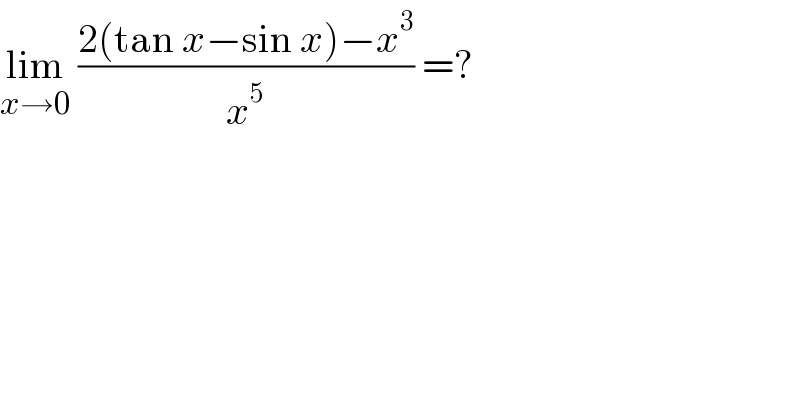 | ||
Answered by liberty last updated on 04/Feb/21 | ||
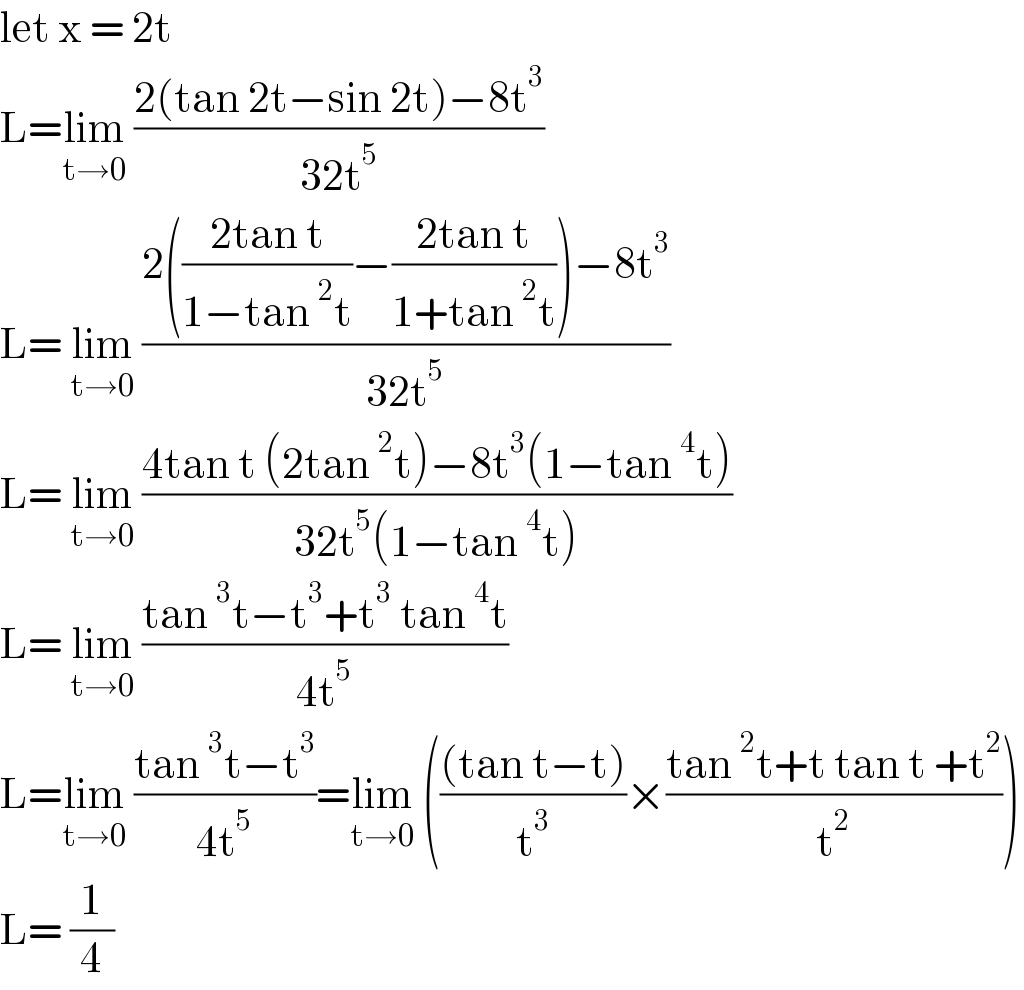 | ||
| ||
Answered by bemath last updated on 04/Feb/21 | ||
![= lim_(x→0) ((2[(x+(x^3 /3)+((2x^5 )/(15)))−(x−(x^3 /6)+(x^5 /(120)))]−x^3 )/x^5 ) = lim_(x→0) ((2((x^3 /2)+((15x^5 )/(120)))−x^3 )/x^5 )=(1/4)](Q131394.png) | ||
| ||