Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 131405 by bramlexs22 last updated on 04/Feb/21

…… super cooles Integral ⋰⋰ ∫_0 ^( ∞) (dx/((1+x^2 )^2 )) =?

$$ \\ $$$$\:\:\ldots\ldots\:\:\mathrm{super}\:\mathrm{cooles}\:\mathrm{Integral}\:\iddots\iddots \\ $$$$\:\int_{\mathrm{0}} ^{\:\infty} \frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=? \\ $$

Commented by bramlexs22 last updated on 04/Feb/21

→→⌣→→ok alle antworten sind super

$$ \\ $$$$\rightarrow\rightarrow\smile\rightarrow\rightarrow\mathrm{ok}\:\mathrm{alle}\:\mathrm{antworten}\:\mathrm{sind}\:\mathrm{super} \\ $$

Commented by Dwaipayan Shikari last updated on 04/Feb/21

For General ∫_0 ^∞ (dx/((1+x^n )^n ))=((Γ(n−(1/n))Γ((1/n)))/(n!)) n≠0 ,1 ∫_0 ^∞ (dx/((1+x^2 )^2 ))=((Γ((3/2))Γ((1/2)))/(2!))=(π/4) ∫_0 ^∞ (dx/((1+x^3 )^3 ))=((Γ((2/3))Γ((1/3)))/6).(5/3).(2/3)=((10π)/(27(√3))) ∫_0 ^∞ (dx/((1+x^4 )^4 ))=((231π)/(256(√2))) ∫_0 ^∞ (dx/((1+x^5 )^5 ))=((2054(√2))/( 9375(√(5−(√5)))))π ...

$${For}\:{General}\:\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\left(\mathrm{1}+{x}^{{n}} \right)^{{n}} }=\frac{\Gamma\left({n}−\frac{\mathrm{1}}{{n}}\right)\Gamma\left(\frac{\mathrm{1}}{{n}}\right)}{{n}!}\:\:\:{n}\neq\mathrm{0}\:,\mathrm{1} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }=\frac{\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}!}=\frac{\pi}{\mathrm{4}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\mathrm{3}} }=\frac{\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)}{\mathrm{6}}.\frac{\mathrm{5}}{\mathrm{3}}.\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{10}\pi}{\mathrm{27}\sqrt{\mathrm{3}}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{4}} \right)^{\mathrm{4}} }=\frac{\mathrm{231}\pi}{\mathrm{256}\sqrt{\mathrm{2}}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{5}} \right)^{\mathrm{5}} }=\frac{\mathrm{2054}\sqrt{\mathrm{2}}}{\:\mathrm{9375}\sqrt{\mathrm{5}−\sqrt{\mathrm{5}}}}\pi \\ $$$$... \\ $$

Answered by mnjuly1970 last updated on 04/Feb/21

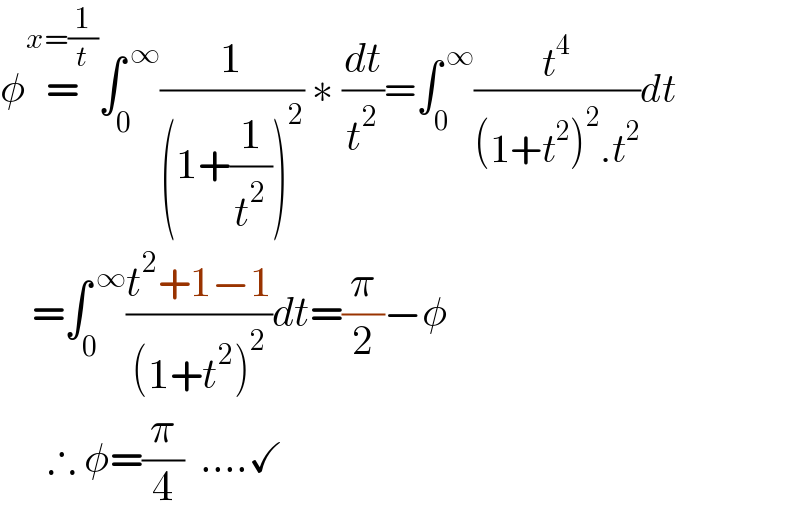
φ=^(x=(1/t)) ∫_0 ^( ∞) (1/((1+(1/t^2 ))^2 )) ∗ (dt/t^2 )=∫_0 ^( ∞) (t^4 /((1+t^2 )^2 .t^2 ))dt =∫_0 ^( ∞) ((t^2 +1−1)/((1+t^2 )^2 ))dt=(π/2)−φ ∴ φ=(π/4) ....✓

$$\phi\overset{{x}=\frac{\mathrm{1}}{{t}}} {=}\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{1}}{\left(\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)^{\mathrm{2}} }\:\ast\:\frac{{dt}}{{t}^{\mathrm{2}} }=\int_{\mathrm{0}} ^{\:\infty} \frac{{t}^{\mathrm{4}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} .{t}^{\mathrm{2}} }{dt} \\ $$$$\:\:\:\:=\int_{\mathrm{0}} ^{\:\infty} \frac{{t}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}=\frac{\pi}{\mathrm{2}}−\phi \\ $$$$\:\:\:\:\:\:\therefore\:\phi=\frac{\pi}{\mathrm{4}}\:\:....\checkmark \\ $$

Answered by Ar Brandon last updated on 04/Feb/21

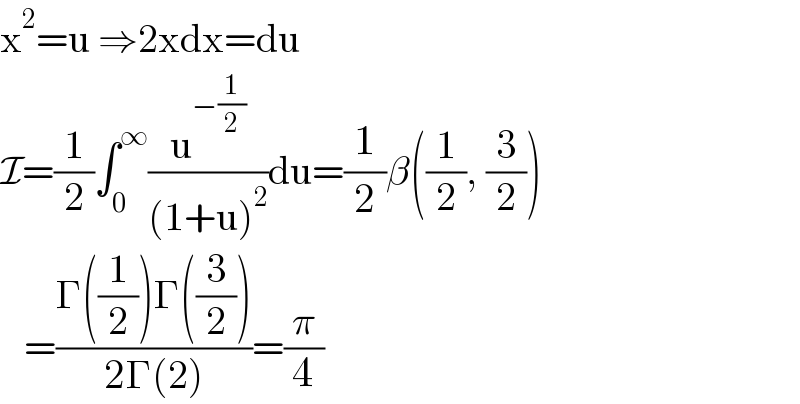
x^2 =u ⇒2xdx=du I=(1/2)∫_0 ^∞ (u^(−(1/2)) /((1+u)^2 ))du=(1/2)β((1/2), (3/2)) =((Γ((1/2))Γ((3/2)))/(2Γ(2)))=(π/4)

$$\mathrm{x}^{\mathrm{2}} =\mathrm{u}\:\Rightarrow\mathrm{2xdx}=\mathrm{du} \\ $$$$\mathcal{I}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{u}^{−\frac{\mathrm{1}}{\mathrm{2}}} }{\left(\mathrm{1}+\mathrm{u}\right)^{\mathrm{2}} }\mathrm{du}=\frac{\mathrm{1}}{\mathrm{2}}\beta\left(\frac{\mathrm{1}}{\mathrm{2}},\:\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$\:\:\:=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\mathrm{2}\Gamma\left(\mathrm{2}\right)}=\frac{\pi}{\mathrm{4}} \\ $$

Answered by mnjuly1970 last updated on 04/Feb/21

φ=∫_0 ^( ∞) (dx/((1+x^2 )^2 ))=^(x^2 =t) (1/2)∫_0 ^( ∞) (t^((−1)/2) /((1+t)^2 ))dt =(1/2)∫_0 ^( ∞) (t^((1/2)−1) /((1+t)^2 ))dt=(1/2)β((1/2) ,(3/2)) =(1/2) ((Γ((1/2))Γ((3/2)))/(Γ(2)))=(1/4) Γ^2 ((1/2))=(π/4)..✓

$$\: \\ $$$$\:\:\phi=\int_{\mathrm{0}} ^{\:\infty} \frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\overset{{x}^{\mathrm{2}} ={t}} {=}\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\infty} \frac{{t}^{\frac{−\mathrm{1}}{\mathrm{2}}} }{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\infty} \frac{{t}^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} }{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt}=\frac{\mathrm{1}}{\mathrm{2}}\beta\left(\frac{\mathrm{1}}{\mathrm{2}}\:,\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{2}\right)}=\frac{\mathrm{1}}{\mathrm{4}}\:\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\pi}{\mathrm{4}}..\checkmark \\ $$

Answered by mathmax by abdo last updated on 04/Feb/21

I =∫_0 ^∞ (dx/((1+x^2 )^2 )) ⇒I=_(x=tant) ∫_0 ^(π/2) (((1+tan^2 t))/((1+tan^2 t)^2 ))dt =∫_0 ^(π/2) (dt/(1+tan^2 t)) =∫_0 ^(π/2) cos^2 t dt =∫_0 ^(π/2) ((1+cos(2t))/2)dt =(π/4)+(1/4)[sin(2t)]_0 ^(π/2) =(π/4)+0 ⇒ I=(π/4)

$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\:\Rightarrow\mathrm{I}=_{\mathrm{x}=\mathrm{tant}} \:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{t}\right)}{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{t}\right)^{\mathrm{2}} }\mathrm{dt}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{t}} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{2}} \mathrm{t}\:\mathrm{dt}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2t}\right)}{\mathrm{2}}\mathrm{dt}\:=\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{sin}\left(\mathrm{2t}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\frac{\pi}{\mathrm{4}}+\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{I}=\frac{\pi}{\mathrm{4}} \\ $$

Answered by mathmax by abdo last updated on 04/Feb/21

parametric method let f(a) =∫_0 ^∞ (dx/(x^2 +a^2 )) with a>0 ⇒ f^′ (a) =−∫_0 ^∞ ((2a)/((x^2 +a^2 )^2 ))dx ⇒∫_0 ^∞ (dx/((x^2 +a^2 )^2 ))=−(1/(2a))f^′ (a) ⇒∫_0 ^∞ (dx/((x^2 +1)^2 ))=−(1/2)f^′ (1) we have f(a) =_(x=az) ∫_0 ^∞ ((adz)/(a^2 (1+z^2 ))) =(1/a)∫_0 ^∞ (dz/(1+z^2 )) =(π/(2a)) ⇒f^′ (a) =−(π/(2a^2 )) ⇒f^′ (1)=−(π/2) ⇒ ∫_0 ^∞ (dx/((x^2 +1)^2 ))=−(1/2)(−(π/2))=(π/4)

$$\mathrm{parametric}\:\mathrm{method}\:\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }\:\:\mathrm{with}\:\mathrm{a}>\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)\:=−\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2a}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{2a}}\mathrm{f}^{'} \left(\mathrm{a}\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{f}^{'} \left(\mathrm{1}\right)\:\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\mathrm{a}\right)\:=_{\mathrm{x}=\mathrm{az}} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{adz}}{\mathrm{a}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dz}}{\mathrm{1}+\mathrm{z}^{\mathrm{2}} }\:=\frac{\pi}{\mathrm{2a}}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)\:=−\frac{\pi}{\mathrm{2a}^{\mathrm{2}} }\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{1}\right)=−\frac{\pi}{\mathrm{2}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{\pi}{\mathrm{2}}\right)=\frac{\pi}{\mathrm{4}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com