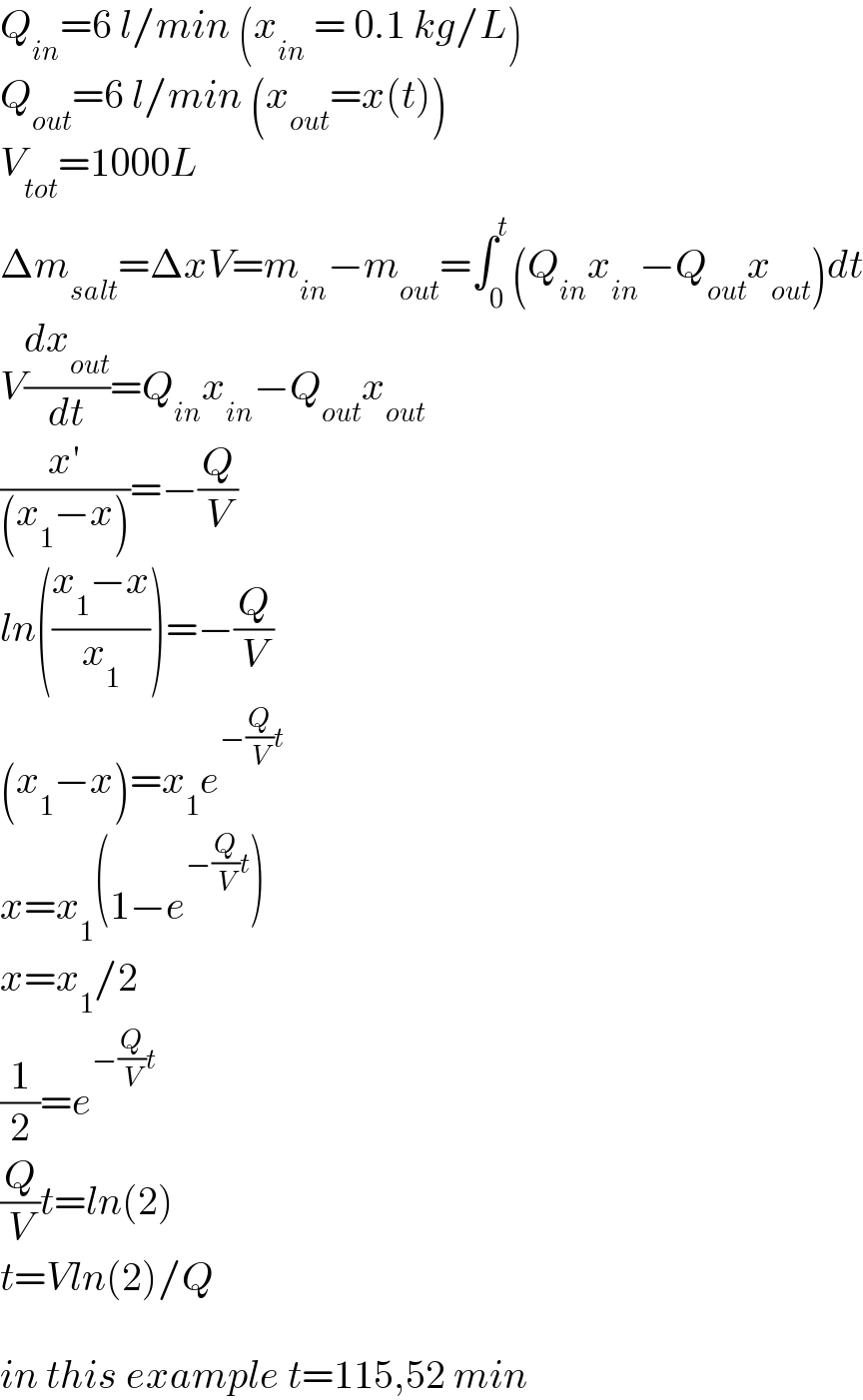Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 131470 by bemath last updated on 05/Feb/21

Consider a large tank holding 1000 L of pure water into which a brine solution of salt begins to flow at constant rate of 6L/min. The solution inside the tank is kept well stirred and is flowing out of the tank at rate of 6L/min. If the concentration of salt in the brine entering the tank is 0.1 kg/L, determine when the concentration of salt in the tank will reach 0.05 kg/L

$${Consider}\:{a}\:{large}\:{tank}\:{holding} \\ $$$$\mathrm{1000}\:{L}\:{of}\:{pure}\:{water}\:{into} \\ $$$${which}\:{a}\:{brine}\:{solution}\:{of} \\ $$$${salt}\:{begins}\:{to}\:{flow}\:{at}\:{constant} \\ $$$${rate}\:{of}\:\mathrm{6}{L}/{min}.\:{The}\:{solution} \\ $$$${inside}\:{the}\:{tank}\:{is}\:{kept}\:{well} \\ $$$${stirred}\:{and}\:{is}\:{flowing}\:{out}\:{of} \\ $$$${the}\:{tank}\:{at}\:{rate}\:{of}\:\mathrm{6}{L}/{min}. \\ $$$${If}\:{the}\:{concentration}\:{of}\:{salt} \\ $$$${in}\:{the}\:{brine}\:{entering}\:{the}\:{tank} \\ $$$${is}\:\mathrm{0}.\mathrm{1}\:{kg}/{L},\:{determine}\:{when} \\ $$$${the}\:{co}\mathrm{n}{centration}\:{of}\:{salt} \\ $$$${in}\:{the}\:{tank}\:{will}\:{reach}\:\mathrm{0}.\mathrm{05}\:{kg}/{L} \\ $$$$ \\ $$

Commented by bemath last updated on 05/Feb/21

thank all master

$$\mathrm{thank}\:\mathrm{all}\:\mathrm{master} \\ $$

Answered by EDWIN88 last updated on 05/Feb/21

we conclude that the input rate of salt into the tank is (6L/min)×(0.1 kg/min)=0.6 kg/min out put rate of salt is (6L/min) [ ((x(t))/(1000)) kg/L ] = ((3x(t))/(500)) kg/min where x(t) denote the mass of salt in tank at time t ⇔ (dx/dt) = 0.6−((3x)/(500)) ; x(0)=0 ⇔ (dx/(100−x)) = (3/(500)) dt ; ln ∣100−x∣=−(3/(500))t+c ⇔100−x(t)=λe^(−(3/(500))t) ; t=0 ;x(0)=0 ⇒ 100=λ ; 100−x(t)=100e^(−(3/(500)) t) ⇔x(t) = 100(1−e^(−((3t)/(500))) ) ((x(t))/(1000)) = 0.1(1−e^(−((3t)/(500))) ) kg/L to determine when the concentration of salt is 0.05 kg/L this gives 0.1(1−e^(−((3t)/(500))) )= 0.05 ; e^(−((3t)/(500))) = 0.5 t = ((500.ln 2)/3) ≈ 115.52 min

$$\mathrm{we}\:\mathrm{conclude}\:\mathrm{that}\:\mathrm{the}\:\mathrm{input}\:\mathrm{rate}\:\mathrm{of}\:\mathrm{salt}\:\mathrm{into} \\ $$$$\mathrm{the}\:\mathrm{tank}\:\mathrm{is}\:\left(\mathrm{6L}/\mathrm{min}\right)×\left(\mathrm{0}.\mathrm{1}\:\mathrm{kg}/\mathrm{min}\right)=\mathrm{0}.\mathrm{6}\:\mathrm{kg}/\mathrm{min} \\ $$$$\mathrm{out}\:\mathrm{put}\:\mathrm{rate}\:\mathrm{of}\:\mathrm{salt}\:\mathrm{is}\:\left(\mathrm{6L}/\mathrm{min}\right)\:\left[\:\frac{\mathrm{x}\left(\mathrm{t}\right)}{\mathrm{1000}}\:\mathrm{kg}/\mathrm{L}\:\right]\:=\:\frac{\mathrm{3x}\left(\mathrm{t}\right)}{\mathrm{500}}\:\mathrm{kg}/\mathrm{min} \\ $$$$\mathrm{where}\:\mathrm{x}\left(\mathrm{t}\right)\:\mathrm{denote}\:\mathrm{the}\:\mathrm{mass}\:\mathrm{of}\:\mathrm{salt}\:\mathrm{in}\:\mathrm{tank}\:\mathrm{at}\:\mathrm{time}\:\mathrm{t} \\ $$$$\Leftrightarrow\:\frac{\mathrm{dx}}{\mathrm{dt}}\:=\:\mathrm{0}.\mathrm{6}−\frac{\mathrm{3x}}{\mathrm{500}}\:;\:\mathrm{x}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\:\Leftrightarrow\:\frac{\mathrm{dx}}{\mathrm{100}−\mathrm{x}}\:=\:\frac{\mathrm{3}}{\mathrm{500}}\:\mathrm{dt}\:;\:\mathrm{ln}\:\mid\mathrm{100}−\mathrm{x}\mid=−\frac{\mathrm{3}}{\mathrm{500}}\mathrm{t}+\mathrm{c} \\ $$$$\Leftrightarrow\mathrm{100}−\mathrm{x}\left(\mathrm{t}\right)=\lambda\mathrm{e}^{−\frac{\mathrm{3}}{\mathrm{500}}\mathrm{t}} \:;\:\mathrm{t}=\mathrm{0}\:;\mathrm{x}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{100}=\lambda\:;\:\mathrm{100}−\mathrm{x}\left(\mathrm{t}\right)=\mathrm{100e}^{−\frac{\mathrm{3}}{\mathrm{500}}\:\mathrm{t}} \\ $$$$\Leftrightarrow\mathrm{x}\left(\mathrm{t}\right)\:=\:\mathrm{100}\left(\mathrm{1}−\mathrm{e}^{−\frac{\mathrm{3t}}{\mathrm{500}}} \:\right) \\ $$$$\:\frac{\mathrm{x}\left(\mathrm{t}\right)}{\mathrm{1000}}\:=\:\mathrm{0}.\mathrm{1}\left(\mathrm{1}−\mathrm{e}^{−\frac{\mathrm{3t}}{\mathrm{500}}} \:\right)\:\mathrm{kg}/\mathrm{L} \\ $$$$\:\mathrm{to}\:\mathrm{determine}\:\mathrm{when}\:\mathrm{the}\:\mathrm{concentration}\:\mathrm{of} \\ $$$$\mathrm{salt}\:\mathrm{is}\:\mathrm{0}.\mathrm{05}\:\mathrm{kg}/\mathrm{L}\:\:\mathrm{this}\:\mathrm{gives}\: \\ $$$$\:\mathrm{0}.\mathrm{1}\left(\mathrm{1}−\mathrm{e}^{−\frac{\mathrm{3t}}{\mathrm{500}}} \:\right)=\:\mathrm{0}.\mathrm{05}\:;\:\mathrm{e}^{−\frac{\mathrm{3t}}{\mathrm{500}}} \:=\:\mathrm{0}.\mathrm{5} \\ $$$$\:\mathrm{t}\:=\:\frac{\mathrm{500}.\mathrm{ln}\:\mathrm{2}}{\mathrm{3}}\:\approx\:\mathrm{115}.\mathrm{52}\:\mathrm{min} \\ $$

Answered by mr W last updated on 05/Feb/21

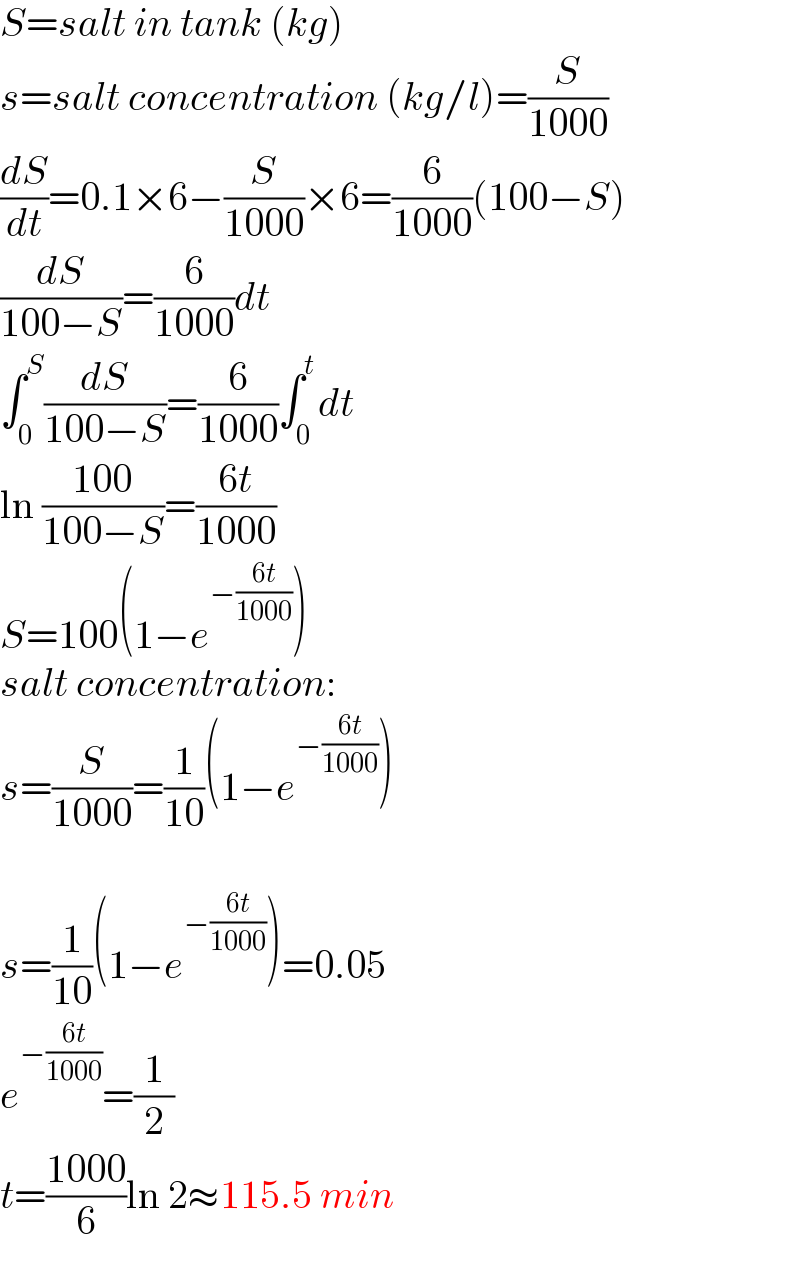
S=salt in tank (kg) s=salt concentration (kg/l)=(S/(1000)) (dS/dt)=0.1×6−(S/(1000))×6=(6/(1000))(100−S) (dS/(100−S))=(6/(1000))dt ∫_0 ^S (dS/(100−S))=(6/(1000))∫_0 ^t dt ln ((100)/(100−S))=((6t)/(1000)) S=100(1−e^(−((6t)/(1000))) ) salt concentration: s=(S/(1000))=(1/(10))(1−e^(−((6t)/(1000))) ) s=(1/(10))(1−e^(−((6t)/(1000))) )=0.05 e^(−((6t)/(1000))) =(1/2) t=((1000)/6)ln 2≈115.5 min

$${S}={salt}\:{in}\:{tank}\:\left({kg}\right) \\ $$$${s}={salt}\:{concentration}\:\left({kg}/{l}\right)=\frac{{S}}{\mathrm{1000}} \\ $$$$\frac{{dS}}{{dt}}=\mathrm{0}.\mathrm{1}×\mathrm{6}−\frac{{S}}{\mathrm{1000}}×\mathrm{6}=\frac{\mathrm{6}}{\mathrm{1000}}\left(\mathrm{100}−{S}\right) \\ $$$$\frac{{dS}}{\mathrm{100}−{S}}=\frac{\mathrm{6}}{\mathrm{1000}}{dt} \\ $$$$\int_{\mathrm{0}} ^{{S}} \frac{{dS}}{\mathrm{100}−{S}}=\frac{\mathrm{6}}{\mathrm{1000}}\int_{\mathrm{0}} ^{{t}} {dt} \\ $$$$\mathrm{ln}\:\frac{\mathrm{100}}{\mathrm{100}−{S}}=\frac{\mathrm{6}{t}}{\mathrm{1000}} \\ $$$${S}=\mathrm{100}\left(\mathrm{1}−{e}^{−\frac{\mathrm{6}{t}}{\mathrm{1000}}} \right) \\ $$$${salt}\:{concentration}: \\ $$$${s}=\frac{{S}}{\mathrm{1000}}=\frac{\mathrm{1}}{\mathrm{10}}\left(\mathrm{1}−{e}^{−\frac{\mathrm{6}{t}}{\mathrm{1000}}} \right) \\ $$$$ \\ $$$${s}=\frac{\mathrm{1}}{\mathrm{10}}\left(\mathrm{1}−{e}^{−\frac{\mathrm{6}{t}}{\mathrm{1000}}} \right)=\mathrm{0}.\mathrm{05} \\ $$$${e}^{−\frac{\mathrm{6}{t}}{\mathrm{1000}}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${t}=\frac{\mathrm{1000}}{\mathrm{6}}\mathrm{ln}\:\mathrm{2}\approx\mathrm{115}.\mathrm{5}\:{min} \\ $$

Answered by TheSupreme last updated on 05/Feb/21

Q_(in) =6 l/min (x_(in) = 0.1 kg/L) Q_(out) =6 l/min (x_(out) =x(t)) V_(tot) =1000L Δm_(salt) =ΔxV=m_(in) −m_(out) =∫_0 ^t (Q_(in) x_(in) −Q_(out) x_(out) )dt V(dx_(out) /dt)=Q_(in) x_(in) −Q_(out) x_(out) ((x′)/((x_1 −x)))=−(Q/V) ln(((x_1 −x)/x_1 ))=−(Q/V) (x_1 −x)=x_1 e^(−(Q/V)t) x=x_1 (1−e^(−(Q/V)t) ) x=x_1 /2 (1/2)=e^(−(Q/V)t) (Q/V)t=ln(2) t=Vln(2)/Q in this example t=115,52 min

$${Q}_{{in}} =\mathrm{6}\:{l}/{min}\:\left({x}_{{in}} \:=\:\mathrm{0}.\mathrm{1}\:{kg}/{L}\right) \\ $$$${Q}_{{out}} =\mathrm{6}\:{l}/{min}\:\left({x}_{{out}} ={x}\left({t}\right)\right) \\ $$$${V}_{{tot}} =\mathrm{1000}{L} \\ $$$$\Delta{m}_{{salt}} =\Delta{xV}={m}_{{in}} −{m}_{{out}} =\int_{\mathrm{0}} ^{{t}} \left({Q}_{{in}} {x}_{{in}} −{Q}_{{out}} {x}_{{out}} \right){dt} \\ $$$${V}\frac{{dx}_{{out}} }{{dt}}={Q}_{{in}} {x}_{{in}} −{Q}_{{out}} {x}_{{out}} \\ $$$$\frac{{x}'}{\left({x}_{\mathrm{1}} −{x}\right)}=−\frac{{Q}}{{V}} \\ $$$${ln}\left(\frac{{x}_{\mathrm{1}} −{x}}{{x}_{\mathrm{1}} }\right)=−\frac{{Q}}{{V}} \\ $$$$\left({x}_{\mathrm{1}} −{x}\right)={x}_{\mathrm{1}} {e}^{−\frac{{Q}}{{V}}{t}} \\ $$$${x}={x}_{\mathrm{1}} \left(\mathrm{1}−{e}^{−\frac{{Q}}{{V}}{t}} \right) \\ $$$${x}={x}_{\mathrm{1}} /\mathrm{2} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}={e}^{−\frac{{Q}}{{V}}{t}} \\ $$$$\frac{{Q}}{{V}}{t}={ln}\left(\mathrm{2}\right) \\ $$$${t}={Vln}\left(\mathrm{2}\right)/{Q} \\ $$$$ \\ $$$${in}\:{this}\:{example}\:{t}=\mathrm{115},\mathrm{52}\:{min} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com