Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 131620 by mohammad17 last updated on 06/Feb/21

Answered by Dwaipayan Shikari last updated on 06/Feb/21

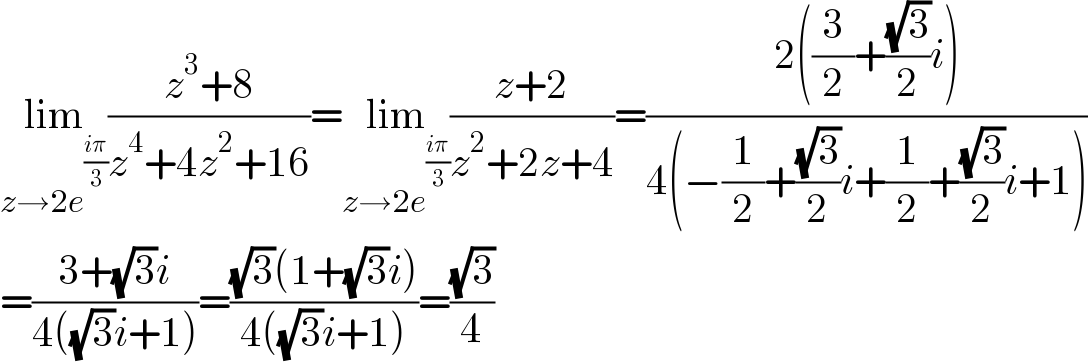
lim_(z→2e^((iπ)/3) ) ((z^3 +8)/(z^4 +4z^2 +16))=lim_(z→2e^((iπ)/3) ) ((z+2)/(z^2 +2z+4))=((2((3/2)+((√3)/2)i))/(4(−(1/2)+((√3)/2)i+(1/2)+((√3)/2)i+1))) =((3+(√3)i)/(4((√3)i+1)))=(((√3)(1+(√3)i))/(4((√3)i+1)))=((√3)/4)

$$\underset{{z}\rightarrow\mathrm{2}{e}^{\frac{{i}\pi}{\mathrm{3}}} } {\mathrm{lim}}\frac{{z}^{\mathrm{3}} +\mathrm{8}}{{z}^{\mathrm{4}} +\mathrm{4}{z}^{\mathrm{2}} +\mathrm{16}}=\underset{{z}\rightarrow\mathrm{2}{e}^{\frac{{i}\pi}{\mathrm{3}}} } {\mathrm{lim}}\frac{{z}+\mathrm{2}}{{z}^{\mathrm{2}} +\mathrm{2}{z}+\mathrm{4}}=\frac{\mathrm{2}\left(\frac{\mathrm{3}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i}\right)}{\mathrm{4}\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{3}+\sqrt{\mathrm{3}}{i}}{\mathrm{4}\left(\sqrt{\mathrm{3}}{i}+\mathrm{1}\right)}=\frac{\sqrt{\mathrm{3}}\left(\mathrm{1}+\sqrt{\mathrm{3}}{i}\right)}{\mathrm{4}\left(\sqrt{\mathrm{3}}{i}+\mathrm{1}\right)}=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$

Answered by mathmax by abdo last updated on 06/Feb/21

(2e^((iπ)/3) )^3 +8 =8e^(iπ) +8 =−8+8=0 (2e^((iπ)/3) )^4 +4(2e^((iπ)/3) )^2 +16 =16 e^(i((4π)/3)) +16e^((i2π)/3) +16 =16{1+e^((i2π)/3) +(e^((i2π)/3) )^2 } =16.((1−(e^((i2π)/3) )^3 )/(1−e^((i2π)/3) ))=0 let use hospital theorem lim_(z→2e^((iπ)/3) ) ((z^3 +8)/(z^4 +4z^2 +16)) =lim_(z→2e^((iπ)/3) ) ((3z^2 )/(4z^3 +8z)) =lim_(z→2e^((iπ)/3) ) ((3z)/(4z^2 +8)) =((6 e^((iπ)/3) )/(8 e^((2iπ)/3) +8)) =(3/4)(e^((iπ)/3) /(1+e^((2iπ)/3) )) =(3/4) (1/(e^((iπ)/3) +e^(−((iπ)/3)) )) =(3/(4×2cos((π/3)))) =(3/(8.(1/2))) =(3/4)

$$\left(\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{3}} +\mathrm{8}\:=\mathrm{8e}^{\mathrm{i}\pi} +\mathrm{8}\:=−\mathrm{8}+\mathrm{8}=\mathrm{0} \\ $$$$\left(\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{4}} \:+\mathrm{4}\left(\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{2}} +\mathrm{16}\:=\mathrm{16}\:\mathrm{e}^{\mathrm{i}\frac{\mathrm{4}\pi}{\mathrm{3}}} \:+\mathrm{16e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} \:+\mathrm{16} \\ $$$$=\mathrm{16}\left\{\mathrm{1}+\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} \:+\left(\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} \right)^{\mathrm{2}} \right\}\:=\mathrm{16}.\frac{\mathrm{1}−\left(\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} \right)^{\mathrm{3}} }{\mathrm{1}−\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} }=\mathrm{0}\:\:\mathrm{let}\:\mathrm{use}\:\mathrm{hospital}\:\mathrm{theorem} \\ $$$$\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} } \:\:\:\frac{\mathrm{z}^{\mathrm{3}} \:+\mathrm{8}}{\mathrm{z}^{\mathrm{4}} \:+\mathrm{4z}^{\mathrm{2}} \:+\mathrm{16}}\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} } \:\:\:\:\frac{\mathrm{3z}^{\mathrm{2}} }{\mathrm{4z}^{\mathrm{3}} \:+\mathrm{8z}}\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} } \:\:\:\frac{\mathrm{3z}}{\mathrm{4z}^{\mathrm{2}} \:+\mathrm{8}} \\ $$$$=\frac{\mathrm{6}\:\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} }{\mathrm{8}\:\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{3}}} \:+\mathrm{8}}\:=\frac{\mathrm{3}}{\mathrm{4}}\frac{\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} }{\mathrm{1}+\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{3}}} }\:=\frac{\mathrm{3}}{\mathrm{4}}\:\frac{\mathrm{1}}{\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \:+\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} }\:=\frac{\mathrm{3}}{\mathrm{4}×\mathrm{2cos}\left(\frac{\pi}{\mathrm{3}}\right)} \\ $$$$=\frac{\mathrm{3}}{\mathrm{8}.\frac{\mathrm{1}}{\mathrm{2}}}\:=\frac{\mathrm{3}}{\mathrm{4}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com