
Question and Answers Forum
Question Number 131688 by liberty last updated on 07/Feb/21
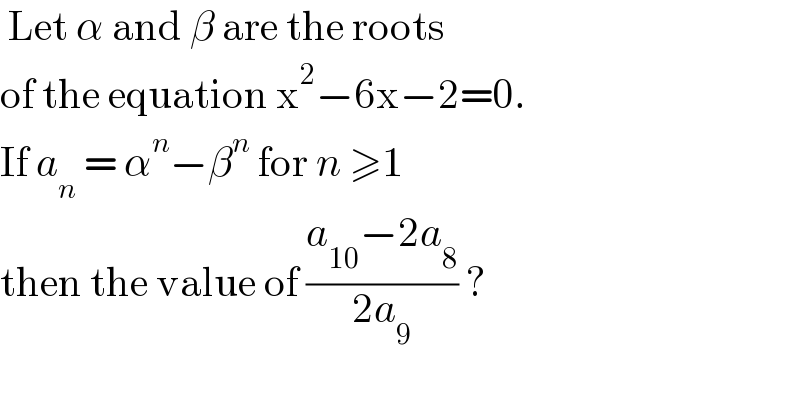
Answered by mathmax by abdo last updated on 07/Feb/21
![x^2 −6x−2=0 →Δ^′ =9+2=11 ⇒x_1 =3+(√(11)) and x_2 =3−(√(11)) a_n =x_1 ^n −x_2 ^n =(3+(√(11)))^n −(3−(√(11)))^n =Σ_(k=0) ^n C_n ^k 3^(n−k) ((√(11)))^k −Σ_(k=0) ^n C_n ^k 3^(n−k) (−(√(11)))^k =Σ_(k=0) ^n C_n ^k 3^(n−k) { 1−(−1)^k )((√(11)))^k =Σ_(p=0) ^([((n−1)/2)]) C_n ^(2p+1) 3^(n−2p−1) 2.((√(11)))^(2p+1) =2(√(11))Σ_(p=0) ^([((n−1)/2)]) C_n ^(2p+1) 3^(n−2p−1) (11)^p ⇒a_(10) =2(√(11))Σ_(p=0) ^4 C_(10) ^(2p+1) 3^(9−2p) (11)^p a_8 =2(√(11))Σ_(p=0) ^3 C_8 ^(2p+1) 3^(7−2p) (11)^p a_9 =2(√(11))Σ_(p=0) ^4 C_9 ^(2p+1) 3^(8−2p) (11)^p rest to finish the calculus...](Q131738.png)
Answered by bemath last updated on 07/Feb/21

| ||
Question and Answers Forum | ||
Question Number 131688 by liberty last updated on 07/Feb/21 | ||
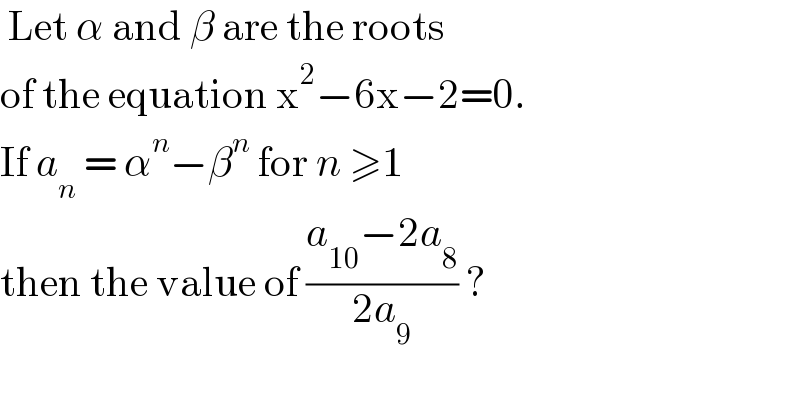 | ||
Answered by mathmax by abdo last updated on 07/Feb/21 | ||
![x^2 −6x−2=0 →Δ^′ =9+2=11 ⇒x_1 =3+(√(11)) and x_2 =3−(√(11)) a_n =x_1 ^n −x_2 ^n =(3+(√(11)))^n −(3−(√(11)))^n =Σ_(k=0) ^n C_n ^k 3^(n−k) ((√(11)))^k −Σ_(k=0) ^n C_n ^k 3^(n−k) (−(√(11)))^k =Σ_(k=0) ^n C_n ^k 3^(n−k) { 1−(−1)^k )((√(11)))^k =Σ_(p=0) ^([((n−1)/2)]) C_n ^(2p+1) 3^(n−2p−1) 2.((√(11)))^(2p+1) =2(√(11))Σ_(p=0) ^([((n−1)/2)]) C_n ^(2p+1) 3^(n−2p−1) (11)^p ⇒a_(10) =2(√(11))Σ_(p=0) ^4 C_(10) ^(2p+1) 3^(9−2p) (11)^p a_8 =2(√(11))Σ_(p=0) ^3 C_8 ^(2p+1) 3^(7−2p) (11)^p a_9 =2(√(11))Σ_(p=0) ^4 C_9 ^(2p+1) 3^(8−2p) (11)^p rest to finish the calculus...](Q131738.png) | ||
| ||
Answered by bemath last updated on 07/Feb/21 | ||
 | ||
| ||