Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 131789 by bemath last updated on 08/Feb/21

$$\mathrm{Let}\phi =\underset{x\to 0}{\lim }\frac{{\mathrm{x}}^4+3({\mathrm{a}}^2-\sqrt{{\mathrm{a}}^4+{\mathrm{x}}^4})}{{\mathrm{x}}^8};\mathrm{a}>0$$ $$\mathrm{If}\phi \mathrm{is}\mathrm{finite}\mathrm{then}$$ $$\left(\mathrm{a}\right)\mathrm{a}=\frac{3}{2}\left(\mathrm{b}\right)\mathrm{a}=\sqrt{\frac{3}{2}}\left(\mathrm{c}\right)\phi =\frac{1}{3}\left(\mathrm{d}\right)\phi =\frac{1}{9}$$

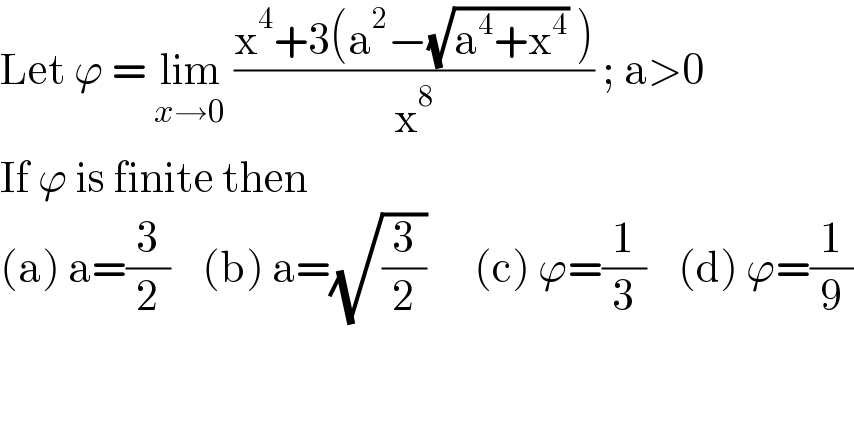
Answered by Dwaipayan Shikari last updated on 08/Feb/21

$$\underset{x\to 0}{\lim }\frac{x^4+3(a^2-a^2(1+\frac{x^4}{2a^4}-\frac{x^8}{8a^8}))}{x^8}=\frac{x^4-\frac{3x^4}{2a^2}+\frac{3x^8}{8a^6}}{x^8}=\phi$$ $$\Rightarrow x^4-\frac{3x^4}{2a^2}=0\Rightarrow 1=\frac{3}{2a^2}\Rightarrow a=\pm \sqrt{\frac{3}{2}}$$ $$\phi =\frac{3}{8a^6}=\frac{3}{8}.\frac{8}{27}=\frac{1}{9}$$

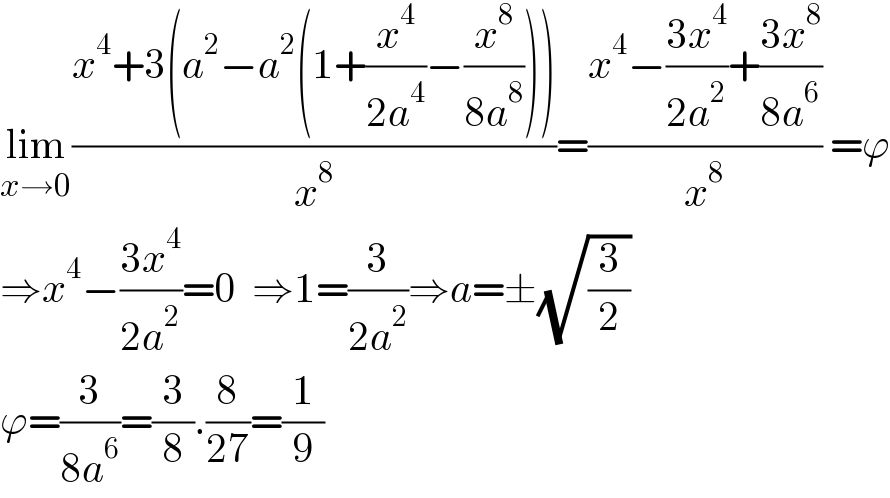
Answered by EDWIN88 last updated on 08/Feb/21

$$\phi =\underset{x\to 0}{\lim }\frac{({\mathrm{x}}^4+{3\mathrm{a}}^2)-3\sqrt{{\mathrm{a}}^4+{\mathrm{x}}^4}}{{\mathrm{x}}^8}=$$ $$\phi =\underset{x\to 0}{\lim }\frac{{({\mathrm{x}}^4+{3\mathrm{a}}^2)}^2-9({\mathrm{a}}^4+{\mathrm{x}}^4)}{{\mathrm{x}}^8(({\mathrm{x}}^4+{3\mathrm{a}}^2)+3\sqrt{{\mathrm{a}}^4+{\mathrm{x}}^4}))}=$$ $$\phi =\frac{1}{{6\mathrm{a}}^2}\times \underset{x\to 0}{\lim }\frac{{\mathrm{x}}^8+{6\mathrm{a}}^2{\mathrm{x}}^4+{9\mathrm{a}}^4-{9\mathrm{a}}^4-{9\mathrm{x}}^4}{{\mathrm{x}}^8}$$ $$\phi =\frac{1}{{6\mathrm{a}}^2}\times \underset{x\to 0}{\lim }\frac{{\mathrm{x}}^8+{\mathrm{x}}^4({6\mathrm{a}}^2-9)}{{\mathrm{x}}^8}$$ $$\mathrm{since}\mathrm{the}\mathrm{value}\mathrm{of}\phi \mathrm{is}\mathrm{finite}\mathrm{it}\mathrm{follows}\mathrm{that}$$ $${6\mathrm{a}}^2-9\mathrm{must}\mathrm{be}\mathrm{is}\mathrm{zero};\mathrm{a}=\sqrt{\frac{3}{2}}$$ $$\mathrm{then}\phi =\frac{1}{6\left(\frac{9}{6}\right)}=\frac{1}{9}$$

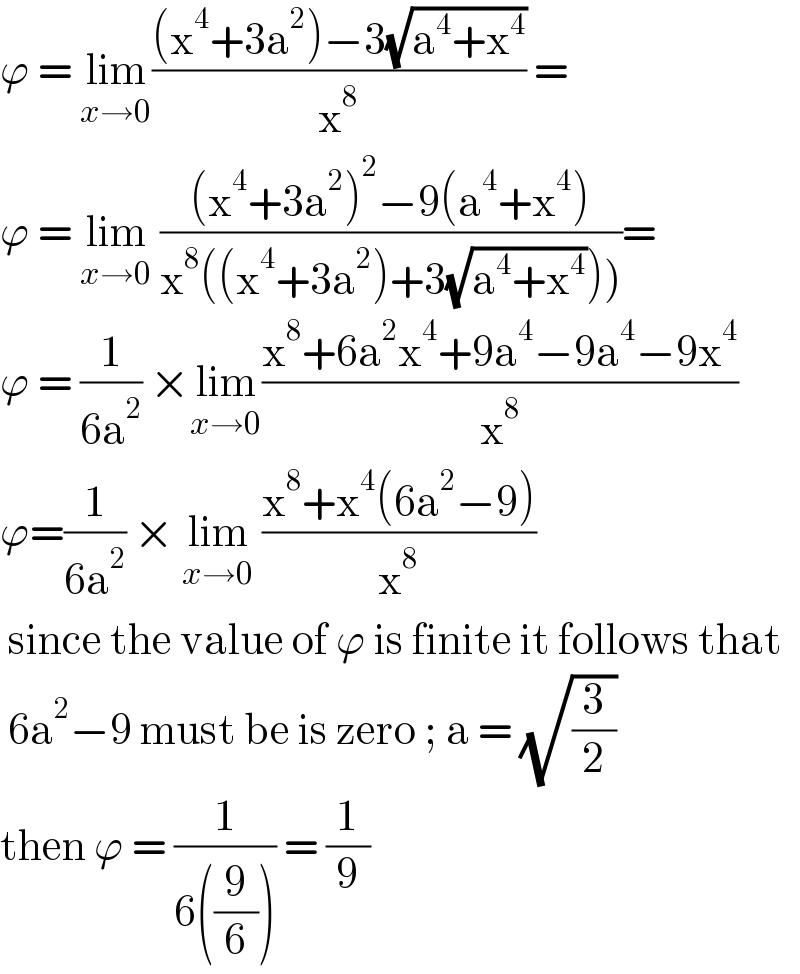
Commented byliberty last updated on 08/Feb/21

$$\mathrm{Hallo}\mathrm{Herr}\mathrm{wie}\mathrm{geht}\mathrm{es}\mathrm{dir}$$

Commented byEDWIN88 last updated on 08/Feb/21

$$$$ $$\mathrm{Hallo}\mathrm{Herr}\mathrm{auch}.\mathrm{Gute}\mathrm{Nachrichten}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com