Question Number 131823 by mr W last updated on 09/Feb/21
Commented by mr W last updated on 10/Feb/21
$${a}\:{small}\:{sphere}\:{of}\:{mass}\:{m}\:{is}\:{released} \\ $$$${from}\:{rest}\:{at}\:{position}\:{as}\:{shown}. \\ $$$${both}\:{the}\:{sphere}\:{and}\:{the}\:{semi}\:{cylinder} \\ $$$${move}\:{without}\:{friction}. \\ $$$${find}\:{the}\:{time}\:{the}\:{sphere}\:{needs}\:{to} \\ $$$${hit}\:{the}\:{ground}. \\ $$
Answered by mr W last updated on 09/Feb/21
Commented by mr W last updated on 10/Feb/21
Commented by mr W last updated on 10/Feb/21
Commented by mr W last updated on 09/Feb/21
$$\theta_{\mathrm{0}} =\mathrm{cos}^{−\mathrm{1}} \frac{{R}−{r}}{{R}+{r}} \\ $$$$\theta_{\mathrm{1}} =\mathrm{sin}^{−\mathrm{1}} \frac{{r}}{{R}+{r}} \\ $$
Commented by mr W last updated on 11/Feb/21
![let ω=(dθ/dt), α=(dω/dt), μ=(M/m) x_Q =r+(R+r)cos θ V=(dx_Q /dt)=ω(dx_Q /dθ)=−(R+r)ω sin θ A=(dV/dt)=−(R+r)(α sin θ+ω^2 cos θ) y_P =(R+r)sin θ v=−(dy_P /dt)=−ω(dy_P /dθ)=−(R+r)ω cos θ a=(dv/dt)=−(R+r)(α cos θ−ω^2 sin θ) ((MV^2 +mv^2 )/2)=mg(R+r)(sin θ_0 −sin θ) (M/m)V^2 +v^2 =2g(R+r)(sin θ_0 −sin θ) [(M/m) sin^2 θ+ cos^2 θ]ω^2 (R+r)^2 =2g(R+r)(sin θ_0 −sin θ) ⇒ω^2 =((2g)/(R+r))×((sin θ_0 −sin θ)/(μ sin^2 θ+ cos^2 θ)) N cos θ=MA ⇒N=−((M(R+r))/(cos θ))(α sin θ+ω^2 cos θ) mg−N sin θ=ma N=((m(g−a))/(sin θ)) ⇒N=((m(R+r))/(sin θ))((g/(R+r))+α cos θ−ω^2 sin θ) ((m(R+r))/(sin θ))((g/(R+r))+α cos θ−ω^2 sin θ)=−((M(R+r))/(cos θ))(α sin θ+ω^2 cos θ) (g/(R+r))+α cos θ−ω^2 sin θ=−((μsin θ)/(cos θ))(α sin θ+ω^2 cos θ) α=−((cos θ)/(μsin^2 θ+cos^2 θ))[(g/(R+r))+(μ−1)sin θ ω^2 ] ⇒α=−(g/(R+r))×((cos θ)/(μsin^2 θ+cos^2 θ))[1+((2(μ−1)sin θ (sin θ_0 −sin θ))/(μ sin^2 θ+ cos^2 θ))] ⇒N=−M(R+r)(((sin θ)/(cos θ))α+ω^2 ) ⇒N=Mg{((sin θ)/(μ sin^2 θ+cos^2 θ))[1+((2(μ−1)sin θ (sin θ_0 −sin θ))/(μ sin^2 θ+ cos^2 θ))]−((2(sin θ_0 −sin θ))/(μ sin^2 θ+ cos^2 θ))} ⇒(N/(mg))=(μ/(μ sin^2 θ+cos^2 θ))[sin θ−((2(sin θ_0 −sin θ))/(μ sin^2 θ+ cos^2 θ))] say N=0 at θ=θ_2 . N=0 ⇒ sin θ−((2(sin θ_0 −sin θ))/(μ sin^2 θ+ cos^2 θ))=0 sin θ=((2(sin θ_0 −sin θ))/((μ−1) sin^2 θ+1)) sin^3 θ+(3/(μ−1)) sin θ−(2/(μ−1)) sin θ_0 =0 if μ=1: 3 sin θ−2 sin θ_0 =0 ⇒sin θ=(2/3) sin θ_0 ⇒θ_2 =sin^(−1) (((2 sin θ_0 )/3)) for μ≠1: let λ=(1/(μ−1))=(m/(M−m)) sin^3 θ+3λ sin θ−2λ sin θ_0 =0 Δ=λ^3 +λ^2 sin^2 θ_0 =λ^2 (λ+sin^2 θ_0 ) for λ+sin^2 θ_0 =(1/(μ−1))+sin^2 θ_0 >0, i.e. for μ>1: sin θ=((λ((√(λ+sin^2 θ_0 ))+sin θ_0 )))^(1/3) −((λ((√(λ+sin^2 θ_0 ))−sin θ_0 )))^(1/3) ⇒θ_2 =sin^(−1) [(((1/(μ−1))((√((1/(μ−1))+sin^2 θ_0 ))+sin θ_0 )))^(1/3) −(((1/(μ−1))((√((1/(μ−1))+sin^2 θ_0 ))−sin θ_0 )))^(1/3) ] for μ<1: sin θ=(2/( (√(1−μ)))) sin [(1/3)sin^(−1) ((√(1−μ)) sin θ_0 )+((2kπ)/3)] ⇒θ_2 =sin^(−1) {(2/( (√(1−μ)))) sin [(1/3)sin^(−1) ((√(1−μ)) sin θ_0 )]} we get θ_2 >θ_1 ,see diagram. that means the sphere losses contact before it hits the ground. after this point the sphere has free fall. T_1 = time for θ from θ_0 to θ_2 T_2 = time for free fall after θ_2 ⇒ω=(dθ/dt)=−(√((2g)/(R+r)))×(√((sin θ_0 −sin θ)/(μ sin^2 θ+ cos^2 θ))) ⇒T_1 =(√((R+r)/(2g)))∫_θ_2 ^θ_0 (√((1+(μ−1) sin^2 θ)/(sin θ_0 −sin θ)))dθ v=(√(2g(R+r)))×cos θ(√((sin θ_0 −sin θ)/(μ sin^2 θ+ cos^2 θ))) v_2 =(√(2g(R+r)))×cos θ_2 (√((sin θ_0 −sin θ_2 )/(μ sin^2 θ_2 + cos^2 θ_2 ))) Δh=(R+r)sin θ_2 −r Δh=v_2 T_2 +(1/2)gT_2 ^2 T_2 =(1/g)((√(v_2 ^2 +2gΔh))−v_2 ) total time: T=T_1 +T_2](Q131846.png)
$${let}\:\omega=\frac{{d}\theta}{{dt}},\:\alpha=\frac{{d}\omega}{{dt}},\:\mu=\frac{{M}}{{m}} \\ $$$${x}_{{Q}} ={r}+\left({R}+{r}\right)\mathrm{cos}\:\theta \\ $$$${V}=\frac{{dx}_{{Q}} }{{dt}}=\omega\frac{{dx}_{{Q}} }{{d}\theta}=−\left({R}+{r}\right)\omega\:\mathrm{sin}\:\theta \\ $$$${A}=\frac{{dV}}{{dt}}=−\left({R}+{r}\right)\left(\alpha\:\mathrm{sin}\:\theta+\omega^{\mathrm{2}} \:\mathrm{cos}\:\theta\right) \\ $$$$ \\ $$$${y}_{{P}} =\left({R}+{r}\right)\mathrm{sin}\:\theta \\ $$$${v}=−\frac{{dy}_{{P}} }{{dt}}=−\omega\frac{{dy}_{{P}} }{{d}\theta}=−\left({R}+{r}\right)\omega\:\mathrm{cos}\:\theta \\ $$$${a}=\frac{{dv}}{{dt}}=−\left({R}+{r}\right)\left(\alpha\:\mathrm{cos}\:\theta−\omega^{\mathrm{2}} \:\mathrm{sin}\:\theta\right) \\ $$$$ \\ $$$$\frac{{MV}^{\mathrm{2}} +{mv}^{\mathrm{2}} }{\mathrm{2}}={mg}\left({R}+{r}\right)\left(\mathrm{sin}\:\theta_{\mathrm{0}} −\mathrm{sin}\:\theta\right) \\ $$$$\frac{{M}}{{m}}{V}^{\mathrm{2}} +{v}^{\mathrm{2}} =\mathrm{2}{g}\left({R}+{r}\right)\left(\mathrm{sin}\:\theta_{\mathrm{0}} −\mathrm{sin}\:\theta\right) \\ $$$$ \\ $$$$\left[\frac{{M}}{{m}}\:\mathrm{sin}^{\mathrm{2}} \:\theta+\:\mathrm{cos}^{\mathrm{2}} \:\theta\right]\omega^{\mathrm{2}} \left({R}+{r}\right)^{\mathrm{2}} =\mathrm{2}{g}\left({R}+{r}\right)\left(\mathrm{sin}\:\theta_{\mathrm{0}} −\mathrm{sin}\:\theta\right) \\ $$$$\Rightarrow\omega^{\mathrm{2}} =\frac{\mathrm{2}{g}}{{R}+{r}}×\frac{\mathrm{sin}\:\theta_{\mathrm{0}} −\mathrm{sin}\:\theta}{\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta+\:\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$ \\ $$$${N}\:\mathrm{cos}\:\theta={MA} \\ $$$$\Rightarrow{N}=−\frac{{M}\left({R}+{r}\right)}{\mathrm{cos}\:\theta}\left(\alpha\:\mathrm{sin}\:\theta+\omega^{\mathrm{2}} \:\mathrm{cos}\:\theta\right) \\ $$$${mg}−{N}\:\mathrm{sin}\:\theta={ma} \\ $$$${N}=\frac{{m}\left({g}−{a}\right)}{\mathrm{sin}\:\theta} \\ $$$$\Rightarrow{N}=\frac{{m}\left({R}+{r}\right)}{\mathrm{sin}\:\theta}\left(\frac{{g}}{{R}+{r}}+\alpha\:\mathrm{cos}\:\theta−\omega^{\mathrm{2}} \:\mathrm{sin}\:\theta\right) \\ $$$$ \\ $$$$\frac{{m}\left({R}+{r}\right)}{\mathrm{sin}\:\theta}\left(\frac{{g}}{{R}+{r}}+\alpha\:\mathrm{cos}\:\theta−\omega^{\mathrm{2}} \:\mathrm{sin}\:\theta\right)=−\frac{{M}\left({R}+{r}\right)}{\mathrm{cos}\:\theta}\left(\alpha\:\mathrm{sin}\:\theta+\omega^{\mathrm{2}} \:\mathrm{cos}\:\theta\right) \\ $$$$\frac{{g}}{{R}+{r}}+\alpha\:\mathrm{cos}\:\theta−\omega^{\mathrm{2}} \:\mathrm{sin}\:\theta=−\frac{\mu\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta}\left(\alpha\:\mathrm{sin}\:\theta+\omega^{\mathrm{2}} \:\mathrm{cos}\:\theta\right) \\ $$$$\alpha=−\frac{\mathrm{cos}\:\theta}{\mu\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{cos}^{\mathrm{2}} \:\theta}\left[\frac{{g}}{{R}+{r}}+\left(\mu−\mathrm{1}\right)\mathrm{sin}\:\theta\:\omega^{\mathrm{2}} \right] \\ $$$$\Rightarrow\alpha=−\frac{{g}}{{R}+{r}}×\frac{\mathrm{cos}\:\theta}{\mu\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{cos}^{\mathrm{2}} \:\theta}\left[\mathrm{1}+\frac{\mathrm{2}\left(\mu−\mathrm{1}\right)\mathrm{sin}\:\theta\:\left(\mathrm{sin}\:\theta_{\mathrm{0}} −\mathrm{sin}\:\theta\right)}{\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta+\:\mathrm{cos}^{\mathrm{2}} \:\theta}\right] \\ $$$$ \\ $$$$\Rightarrow{N}=−{M}\left({R}+{r}\right)\left(\frac{\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta}\alpha+\omega^{\mathrm{2}} \right) \\ $$$$\Rightarrow{N}={Mg}\left\{\frac{\mathrm{sin}\:\theta}{\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{cos}^{\mathrm{2}} \:\theta}\left[\mathrm{1}+\frac{\mathrm{2}\left(\mu−\mathrm{1}\right)\mathrm{sin}\:\theta\:\left(\mathrm{sin}\:\theta_{\mathrm{0}} −\mathrm{sin}\:\theta\right)}{\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta+\:\mathrm{cos}^{\mathrm{2}} \:\theta}\right]−\frac{\mathrm{2}\left(\mathrm{sin}\:\theta_{\mathrm{0}} −\mathrm{sin}\:\theta\right)}{\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta+\:\mathrm{cos}^{\mathrm{2}} \:\theta}\right\} \\ $$$$\Rightarrow\frac{{N}}{{mg}}=\frac{\mu}{\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{cos}^{\mathrm{2}} \:\theta}\left[\mathrm{sin}\:\theta−\frac{\mathrm{2}\left(\mathrm{sin}\:\theta_{\mathrm{0}} −\mathrm{sin}\:\theta\right)}{\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta+\:\mathrm{cos}^{\mathrm{2}} \:\theta}\right] \\ $$$$ \\ $$$${say}\:{N}=\mathrm{0}\:{at}\:\theta=\theta_{\mathrm{2}} . \\ $$$${N}=\mathrm{0}\:\Rightarrow\:\mathrm{sin}\:\theta−\frac{\mathrm{2}\left(\mathrm{sin}\:\theta_{\mathrm{0}} −\mathrm{sin}\:\theta\right)}{\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta+\:\mathrm{cos}^{\mathrm{2}} \:\theta}=\mathrm{0} \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{2}\left(\mathrm{sin}\:\theta_{\mathrm{0}} −\mathrm{sin}\:\theta\right)}{\left(\mu−\mathrm{1}\right)\:\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{1}} \\ $$$$\mathrm{sin}^{\mathrm{3}} \:\theta+\frac{\mathrm{3}}{\mu−\mathrm{1}}\:\mathrm{sin}\:\theta−\frac{\mathrm{2}}{\mu−\mathrm{1}}\:\mathrm{sin}\:\theta_{\mathrm{0}} =\mathrm{0} \\ $$$${if}\:\mu=\mathrm{1}:\: \\ $$$$\mathrm{3}\:\mathrm{sin}\:\theta−\mathrm{2}\:\mathrm{sin}\:\theta_{\mathrm{0}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{sin}\:\theta_{\mathrm{0}} \\ $$$$\Rightarrow\theta_{\mathrm{2}} =\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}\:\mathrm{sin}\:\theta_{\mathrm{0}} }{\mathrm{3}}\right) \\ $$$${for}\:\mu\neq\mathrm{1}: \\ $$$${let}\:\lambda=\frac{\mathrm{1}}{\mu−\mathrm{1}}=\frac{{m}}{{M}−{m}} \\ $$$$\mathrm{sin}^{\mathrm{3}} \:\theta+\mathrm{3}\lambda\:\mathrm{sin}\:\theta−\mathrm{2}\lambda\:\mathrm{sin}\:\theta_{\mathrm{0}} =\mathrm{0} \\ $$$$\Delta=\lambda^{\mathrm{3}} +\lambda^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta_{\mathrm{0}} =\lambda^{\mathrm{2}} \left(\lambda+\mathrm{sin}^{\mathrm{2}} \:\theta_{\mathrm{0}} \right) \\ $$$${for}\:\lambda+\mathrm{sin}^{\mathrm{2}} \:\theta_{\mathrm{0}} =\frac{\mathrm{1}}{\mu−\mathrm{1}}+\mathrm{sin}^{\mathrm{2}} \:\theta_{\mathrm{0}} >\mathrm{0},\:{i}.{e}. \\ $$$${for}\:\mu>\mathrm{1}: \\ $$$$\mathrm{sin}\:\theta=\sqrt[{\mathrm{3}}]{\lambda\left(\sqrt{\lambda+\mathrm{sin}^{\mathrm{2}} \:\theta_{\mathrm{0}} }+\mathrm{sin}\:\theta_{\mathrm{0}} \right)}−\sqrt[{\mathrm{3}}]{\lambda\left(\sqrt{\lambda+\mathrm{sin}^{\mathrm{2}} \:\theta_{\mathrm{0}} }−\mathrm{sin}\:\theta_{\mathrm{0}} \right)} \\ $$$$\Rightarrow\theta_{\mathrm{2}} =\mathrm{sin}^{−\mathrm{1}} \left[\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}}{\mu−\mathrm{1}}\left(\sqrt{\frac{\mathrm{1}}{\mu−\mathrm{1}}+\mathrm{sin}^{\mathrm{2}} \:\theta_{\mathrm{0}} }+\mathrm{sin}\:\theta_{\mathrm{0}} \right)}−\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}}{\mu−\mathrm{1}}\left(\sqrt{\frac{\mathrm{1}}{\mu−\mathrm{1}}+\mathrm{sin}^{\mathrm{2}} \:\theta_{\mathrm{0}} }−\mathrm{sin}\:\theta_{\mathrm{0}} \right)}\right] \\ $$$${for}\:\mu<\mathrm{1}: \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−\mu}}\:\mathrm{sin}\:\left[\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \left(\sqrt{\mathrm{1}−\mu}\:\mathrm{sin}\:\theta_{\mathrm{0}} \right)+\frac{\mathrm{2}{k}\pi}{\mathrm{3}}\right] \\ $$$$\Rightarrow\theta_{\mathrm{2}} =\mathrm{sin}^{−\mathrm{1}} \left\{\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−\mu}}\:\mathrm{sin}\:\left[\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \left(\sqrt{\mathrm{1}−\mu}\:\mathrm{sin}\:\theta_{\mathrm{0}} \right)\right]\right\} \\ $$$${we}\:{get}\:\theta_{\mathrm{2}} >\theta_{\mathrm{1}} ,{see}\:{diagram}. \\ $$$${that}\:{means}\:{the}\:{sphere}\:{losses}\:{contact} \\ $$$${before}\:{it}\:{hits}\:{the}\:{ground}.\:{after}\:{this} \\ $$$${point}\:{the}\:{sphere}\:{has}\:{free}\:{fall}. \\ $$$$ \\ $$$${T}_{\mathrm{1}} =\:{time}\:{for}\:\theta\:{from}\:\theta_{\mathrm{0}} \:{to}\:\theta_{\mathrm{2}} \\ $$$${T}_{\mathrm{2}} =\:{time}\:{for}\:{free}\:{fall}\:{after}\:\theta_{\mathrm{2}} \\ $$$$\Rightarrow\omega=\frac{{d}\theta}{{dt}}=−\sqrt{\frac{\mathrm{2}{g}}{{R}+{r}}}×\sqrt{\frac{\mathrm{sin}\:\theta_{\mathrm{0}} −\mathrm{sin}\:\theta}{\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta+\:\mathrm{cos}^{\mathrm{2}} \:\theta}} \\ $$$$\Rightarrow{T}_{\mathrm{1}} =\sqrt{\frac{{R}+{r}}{\mathrm{2}{g}}}\int_{\theta_{\mathrm{2}} } ^{\theta_{\mathrm{0}} } \sqrt{\frac{\mathrm{1}+\left(\mu−\mathrm{1}\right)\:\mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{sin}\:\theta_{\mathrm{0}} −\mathrm{sin}\:\theta}}{d}\theta \\ $$$$ \\ $$$${v}=\sqrt{\mathrm{2}{g}\left({R}+{r}\right)}×\mathrm{cos}\:\theta\sqrt{\frac{\mathrm{sin}\:\theta_{\mathrm{0}} −\mathrm{sin}\:\theta}{\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta+\:\mathrm{cos}^{\mathrm{2}} \:\theta}} \\ $$$${v}_{\mathrm{2}} =\sqrt{\mathrm{2}{g}\left({R}+{r}\right)}×\mathrm{cos}\:\theta_{\mathrm{2}} \sqrt{\frac{\mathrm{sin}\:\theta_{\mathrm{0}} −\mathrm{sin}\:\theta_{\mathrm{2}} }{\mu\:\mathrm{sin}^{\mathrm{2}} \:\theta_{\mathrm{2}} +\:\mathrm{cos}^{\mathrm{2}} \:\theta_{\mathrm{2}} }} \\ $$$$\Delta{h}=\left({R}+{r}\right)\mathrm{sin}\:\theta_{\mathrm{2}} −{r} \\ $$$$\Delta{h}={v}_{\mathrm{2}} {T}_{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{gT}_{\mathrm{2}} ^{\mathrm{2}} \\ $$$${T}_{\mathrm{2}} =\frac{\mathrm{1}}{{g}}\left(\sqrt{{v}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{2}{g}\Delta{h}}−{v}_{\mathrm{2}} \right) \\ $$$$ \\ $$$${total}\:{time}: \\ $$$${T}={T}_{\mathrm{1}} +{T}_{\mathrm{2}} \\ $$
Commented by mr W last updated on 10/Feb/21
Commented by mr W last updated on 10/Feb/21
$${God}\:{bless}\:{you}\:{too}! \\ $$
Commented by otchereabdullai@gmail.com last updated on 10/Feb/21
$$\mathrm{Amen} \\ $$
Commented by otchereabdullai@gmail.com last updated on 10/Feb/21
$$\mathrm{You}\:\mathrm{are}\:\mathrm{too}\:\mathrm{much}\:\mathrm{prof}\:\mathrm{W}\:\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you} \\ $$
Commented by mr W last updated on 10/Feb/21
Commented by ajfour last updated on 10/Feb/21
$${N}\mathrm{cos}\:\theta={MA} \\ $$$${mg}−{N}\mathrm{sin}\:\theta={ma} \\ $$$${a}\mathrm{sin}\:\theta={A}\mathrm{cos}\:\theta \\ $$$$\Rightarrow\:\:{mg}={ma}+\frac{{MA}\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta} \\ $$$$\Rightarrow\:\:{mg}={ma}+\frac{{Ma}\mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{cos}\:^{\mathrm{2}} \theta} \\ $$$${a}=\frac{{g}}{\mathrm{1}+\lambda\mathrm{tan}\:^{\mathrm{2}} \theta}\:\:\:\:\:\:\:{where}\:\lambda=\frac{{M}}{{m}} \\ $$$${A}=\frac{{g}\mathrm{tan}\:\theta}{\mathrm{1}+\lambda\mathrm{tan}\:^{\mathrm{2}} \theta} \\ $$$$\Rightarrow\:\:{Normal}\:{reaction}\:{N}\:{is}\:{not} \\ $$$${zero}\:\:{before}\:{ball}\:{touches}\:{ground}; \\ $$$${so}\:{it}\:{appears}\:{from}\:{the} \\ $$$${acceleration}\:{expressions}... \\ $$$${What}\:{d}'{ya}\:{think}\:{Sir}? \\ $$$$\frac{{dv}}{{dt}}=\frac{{g}}{\mathrm{1}+\lambda\mathrm{tan}\:^{\mathrm{2}} \theta} \\ $$$${y}=\left({R}+{r}\right)\mathrm{sin}\:\theta \\ $$$${v}=\left(−\frac{{d}\theta}{{dt}}\right)\left({R}+{r}\right)\mathrm{cos}\:\theta \\ $$$$\Rightarrow\int{vdv}=−{g}\left({R}+{r}\right)\int\frac{\mathrm{cos}\:\theta{d}\theta}{\mathrm{1}+\lambda\mathrm{tan}\:^{\mathrm{2}} \theta} \\ $$$$\frac{{v}^{\mathrm{2}} }{\mathrm{2}}={g}\left({R}+{r}\right)\int_{\theta_{\mathrm{0}} } ^{\:\theta} \frac{\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \theta\right){d}\left(\mathrm{sin}\:\theta\right)}{\mathrm{1}+\left(\lambda−\mathrm{1}\right)\mathrm{sin}\:^{\mathrm{2}} \theta} \\ $$$$\frac{{v}^{\mathrm{2}} }{\mathrm{2}}=\frac{{g}\left({R}+{r}\right)}{\lambda−\mathrm{1}}\int\:\frac{\left(\mathrm{1}−{s}^{\mathrm{2}} \right){ds}}{{s}^{\mathrm{2}} +\frac{\mathrm{1}}{\lambda−\mathrm{1}}} \\ $$$$\frac{{v}^{\mathrm{2}} \left(\lambda−\mathrm{1}\right)}{\mathrm{2}{g}\left({R}+{r}\right)}=−\int{ds}+\frac{\mathrm{1}}{\lambda−\mathrm{1}}\int\frac{{ds}}{{s}^{\mathrm{2}} +\frac{\mathrm{1}}{\lambda−\mathrm{1}}} \\ $$$$\left.\frac{{v}^{\mathrm{2}} \left(\lambda−\mathrm{1}\right)}{\mathrm{2}{g}\left({R}+{r}\right)}=−{s}+\frac{\mathrm{1}}{\:\sqrt{\lambda−\mathrm{1}}}\mathrm{tan}^{−\mathrm{1}} \left({s}\sqrt{\lambda−\mathrm{1}}\right)\right) \\ $$$$ \\ $$
Commented by mr W last updated on 10/Feb/21
$${thanks}\:{so}\:{far}\:{sir}! \\ $$$${i}\:{agree}\:{with}\:{v}\:\mathrm{sin}\:\theta={V}\:\mathrm{cos}\:\theta,\:{but}\:{it} \\ $$$${doesn}'{t}\:{follow}\:{that}\:{a}\mathrm{sin}\:\theta={A}\mathrm{cos}\:\theta. \\ $$$${please}\:{recheck}! \\ $$
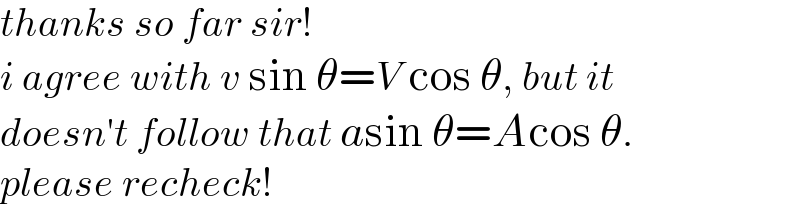
Commented by mr W last updated on 11/Feb/21
