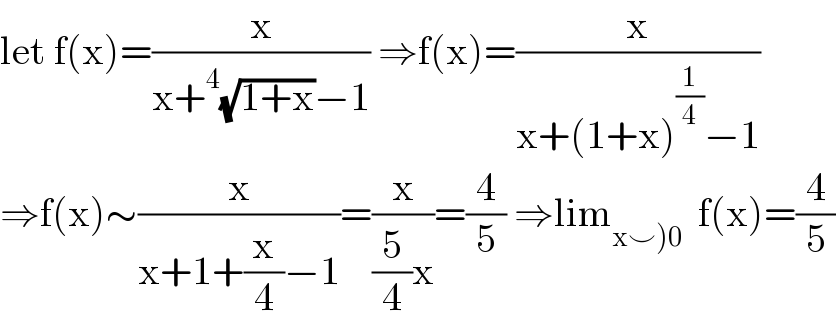Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 131882 by Eric002 last updated on 09/Feb/21

lim_(x→0) (x/(x+((x+1))^(1/4) −1))

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}}{{x}+\sqrt[{\mathrm{4}}]{{x}+\mathrm{1}}−\mathrm{1}} \\ $$

Answered by liberty last updated on 09/Feb/21

L′Ho^ pital L= lim_(x→0) [ (1/(1+(1/(4 (((x+1)^3 ))^(1/4) )))) ]=(1/(1+(1/4)))= (4/5) or lim_(x→0) [ (x/(x+1+(x/4)−1))] = lim_(x→0) ((4x)/(5x))=(4/5)

$$\:\mathrm{L}'\mathrm{H}\ddot {\mathrm{o}pital}\:\mathrm{L}=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left[\:\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}\:\sqrt[{\mathrm{4}}]{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} }}}\:\right]=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}}=\:\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\mathrm{or}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\:\frac{\mathrm{x}}{\mathrm{x}+\mathrm{1}+\frac{\mathrm{x}}{\mathrm{4}}−\mathrm{1}}\right]\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{4x}}{\mathrm{5x}}=\frac{\mathrm{4}}{\mathrm{5}} \\ $$

Commented by Eric002 last updated on 09/Feb/21

how did you get (x/(x+1+(x/4)−1))

$${how}\:{did}\:{you}\:{get}\:\frac{{x}}{{x}+\mathrm{1}+\frac{{x}}{\mathrm{4}}−\mathrm{1}} \\ $$

Commented by EDWIN88 last updated on 09/Feb/21

Bernoulli equation lim_(x→0) (1+f(x))^n ≈ lim_(x→0) (1+n.f(x)) so lim_(x→0) ((1+x))^(1/4) ≈ lim_(x→0) (1+(x/4))

$$\mathrm{Bernoulli}\:\mathrm{equation}\: \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{1}+\mathrm{f}\left(\mathrm{x}\right)\right)^{\mathrm{n}} \:\approx\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+\mathrm{n}.\mathrm{f}\left(\mathrm{x}\right)\right) \\ $$$$\:\mathrm{so}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\sqrt[{\mathrm{4}}]{\mathrm{1}+\mathrm{x}}\:\approx\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{1}+\frac{\mathrm{x}}{\mathrm{4}}\right) \\ $$

Commented by Eric002 last updated on 09/Feb/21

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Answered by EDWIN88 last updated on 09/Feb/21

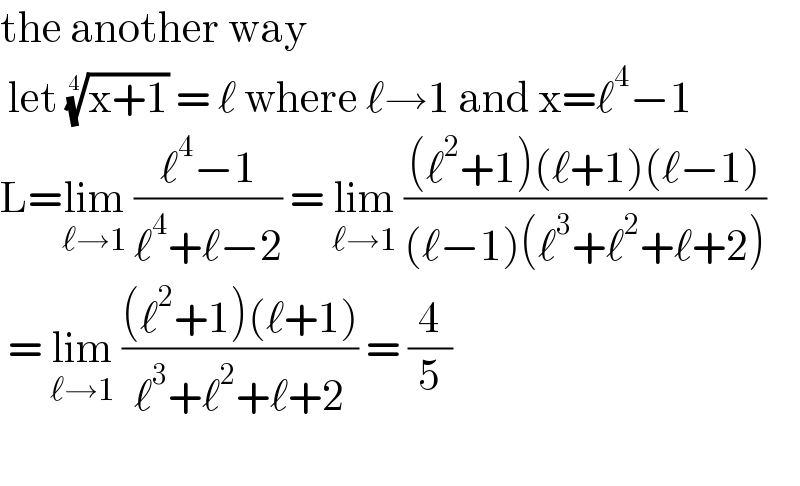
the another way let ((x+1))^(1/4) = ℓ where ℓ→1 and x=ℓ^4 −1 L=lim_(ℓ→1) ((ℓ^4 −1)/(ℓ^4 +ℓ−2)) = lim_(ℓ→1) (((ℓ^2 +1)(ℓ+1)(ℓ−1))/((ℓ−1)(ℓ^3 +ℓ^2 +ℓ+2))) = lim_(ℓ→1) (((ℓ^2 +1)(ℓ+1))/(ℓ^3 +ℓ^2 +ℓ+2)) = (4/5)

$$\mathrm{the}\:\mathrm{another}\:\mathrm{way} \\ $$$$\:\mathrm{let}\:\sqrt[{\mathrm{4}}]{\mathrm{x}+\mathrm{1}}\:=\:\ell\:\mathrm{where}\:\ell\rightarrow\mathrm{1}\:\mathrm{and}\:\mathrm{x}=\ell^{\mathrm{4}} −\mathrm{1} \\ $$$$\mathrm{L}=\underset{\ell\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\ell^{\mathrm{4}} −\mathrm{1}}{\ell^{\mathrm{4}} +\ell−\mathrm{2}}\:=\:\underset{\ell\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left(\ell^{\mathrm{2}} +\mathrm{1}\right)\left(\ell+\mathrm{1}\right)\left(\ell−\mathrm{1}\right)}{\left(\ell−\mathrm{1}\right)\left(\ell^{\mathrm{3}} +\ell^{\mathrm{2}} +\ell+\mathrm{2}\right)}\: \\ $$$$\:=\:\underset{\ell\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left(\ell^{\mathrm{2}} +\mathrm{1}\right)\left(\ell+\mathrm{1}\right)}{\ell^{\mathrm{3}} +\ell^{\mathrm{2}} +\ell+\mathrm{2}}\:=\:\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$ \\ $$

Answered by mathmax by abdo last updated on 10/Feb/21

let f(x)=(x/(x+^4 (√(1+x))−1)) ⇒f(x)=(x/(x+(1+x)^(1/4) −1)) ⇒f(x)∼(x/(x+1+(x/4)−1))=(x/((5/4)x))=(4/5) ⇒lim_(x⌣)0) f(x)=(4/5)

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}}{\mathrm{x}+^{\mathrm{4}} \sqrt{\mathrm{1}+\mathrm{x}}−\mathrm{1}}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}}{\mathrm{x}+\left(\mathrm{1}+\mathrm{x}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} −\mathrm{1}} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\sim\frac{\mathrm{x}}{\mathrm{x}+\mathrm{1}+\frac{\mathrm{x}}{\mathrm{4}}−\mathrm{1}}=\frac{\mathrm{x}}{\frac{\mathrm{5}}{\mathrm{4}}\mathrm{x}}=\frac{\mathrm{4}}{\mathrm{5}}\:\Rightarrow\mathrm{lim}_{\left.\mathrm{x}\smile\right)\mathrm{0}} \:\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{4}}{\mathrm{5}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com